个人项目作业$\cdot$求交点个数
个人项目作业\(\cdot\)求交点个数
一、作业要求简介
本次作业是北航计算机学院软件工程课程的个人项目作业,个人开发能力对于软件开发团队是至关重要的,本项目旨在通过一个求几何图形的交点的需求来使学生学会个人开发的常用技巧,如PSP方法,需求分析,设计文档,编码实现,测试,性能评价等等。
| 项目 | 内容 |
|---|---|
| 本作业属于北航软件工程课程 | 博客园班级博客 |
| 作业要求请点击链接查看 | 个人项目作业 |
| 班级:006 | Sample |
| GitHub地址 | IntersectProject |
| 我在这门课程的目标是 | 获得成为一名软件工程师的能力 |
| 这个作业在哪个具体方面帮助我实现目标 | 总结过去、规划未来 |
二、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 90 | 83 |
| · Estimate | · 估计这个任务需要多少时间 | 90 | 83 |
| Development | 开发 | 830 | 1320 |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 60 |
| · Design Spec | · 生成设计文档 | 60 | 40 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 60 | 60 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 20 |
| · Design | · 具体设计 | 60 | 120 |
| · Coding | · 具体编码 | 240 | 480 |
| · Code Review | · 代码复审 | 0 | 0 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 360 | 540 |
| Reporting | 报告 | 180 | 240 |
| · Test Report | · 测试报告 | 30 | 180 |
| · Size Measurement | · 计算工作量 | 30 | 30 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 120 | 30 |
| 合计 | 1100 | 1560 |
三、解题思路描述
题目需求简述
- 题目需求为,给定若干直线,求其交点个数
- 直线条数
1000 <= N <= 500000 - 交点个数
0 <= h <= 5000000 - 运行时长60s
解题思路
拿到题目首先想到暴力求解,两两计算交点,然后去重。但是这样就是纯\(O(n^2)\)的复杂度,必然TLE的。思来想去呢也没有想到本质上改变最坏复杂度\(O(n^2)\)的算法。于是便在网上查了一些资料,发现网上的题目都有一个重要的限定,不存在三线共点。但是我们这个题目的需求是允许三线共点的,所以并没有什么帮助。
之后看到了交点个数0 <= h <= 5000000的限制,感觉也许最坏复杂度\(O(n^2)\)的算法并不是不可能解的,因为如果有N = 500000条直线不存在三线共点和平行的话,确实会有\(N(N-1)/2\)个交点,但是之所以交点个数有限制 h <= 5000000,就说明存在大量的多线共点和平行。
沿着这个思路想下去,便可以在暴力的\(O(n^2)\)算法基础上考虑将多线共点和平行的情况剪枝掉,剪枝后的具体的时间复杂度比较复杂我没有计算,不过应该是可以满足时间条件的,后文中将对其进行压力测试。
四、设计文档
(一)PipeLine
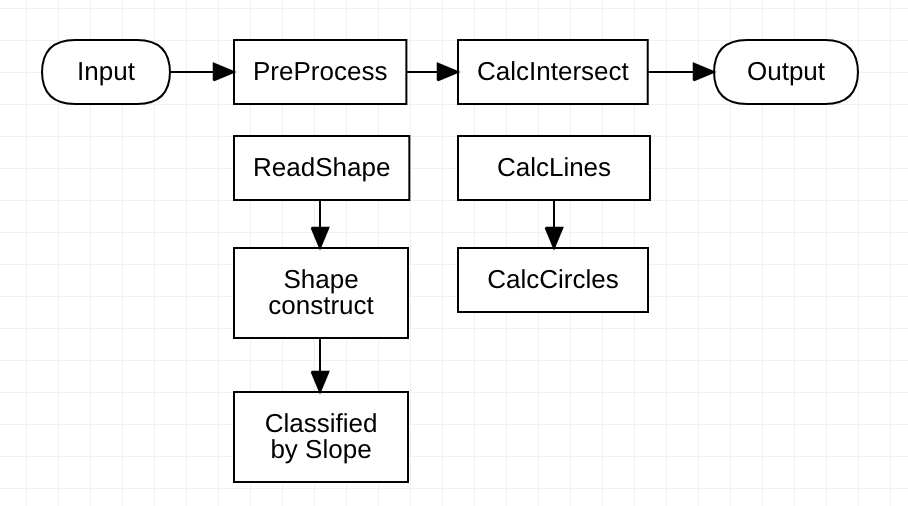
PreProcess
- ReadShape:读取文件接收全部输入的直线和圆
- Shape construct:根据输入构建形状对象,计算直线斜率。
- Classified by Slope:按斜率将直线分组存起来。
CalcIntersect
- CalcLines:计算所有直线之间的交点:
- 依次考虑每个平行组,按每条线遍历计算交点。平行组内的线不用计算交点。
- 查交点表,如果存在,就可以不求同一交点的其他线了。
交点表:Map<点,Set<线>>
维护交点表:新增的交点加入交点表,线加入表中对应的线集
- CalcCircles:所有线算完后,再一个个遍历圆。暴力求其与之前图形的全部交点。
- 计算圆与直线的交点时,可以按如下方法剪枝:
考虑圆与一族平行线的交点,将平行线族的截距排序为b1,b2,b3 \(\cdots\)
若bi开始与圆相离,则大于i的线一定相离,反正小于的情况亦然。
(二)类间关系图UML
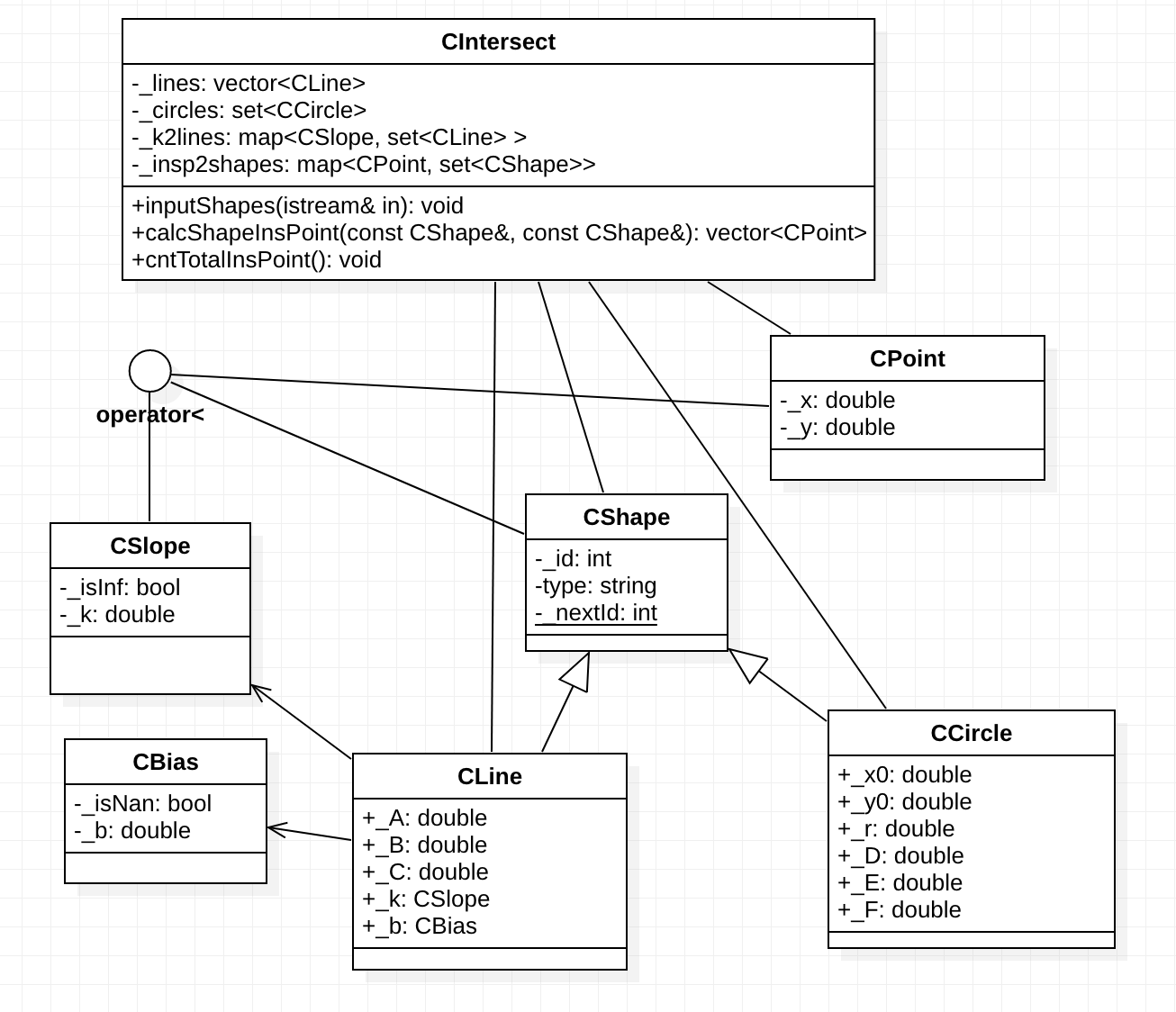
- CIntersect类:实现控制流,方法包含输入、计算两图形交点、计算交点总数
- CShape类:图形类基类,为每个图形实例创建唯一id
- CLine类和CCircle类:继承图形类基类,作用为表示形状代数方程参数。
- 直线方程两种表示方法
- 一般方程:\(Ax + By +C = 0\)
- 斜截方程:\(y = kx + b\)
- 圆方程两种表示
- 一般方程: \(x^2 + y^2 + Dx + Ey +F = 0\)
- 标准方程: \((x-x_0)^2 + (y-y_0)^2 = r^2\)
- CSlope类和CBias类:为解决斜率无穷大设计,isInf和isNan为true时表示直线的斜率为无穷,此时k和b的具体值无效。由于要按斜率分组,CSlope要实现小于运算符。
- CPoint类:表示交点,作为map的key,需要实现小于运算符。
(三)关键函数
- inputShapes: 处理输入函数,直线按斜率分组,放到
map<double, set<CLine>>的_k2lines中
圆直接放到set<CCircle>的_circles里。 - calcShapeInsPoint:求两个图形交点的函数,分三种情况,返回点的vector。
- 直线与直线
- 直线与圆
- 圆与圆
- cntTotalInsPoint: 求所有焦点的函数,按先直线后圆的顺序依次遍历求焦点。已经遍历到的图形加入一个
over集中。- 直线两个剪枝方法:
- 砍平行:依次加入每个平行组,不需计算组内直线交点,只需遍历
over集中其它不平行直线。 - 砍共点:假若ABC共点,按ABC的顺序遍历,先计算了AB,交点为P;之后计算AC时发现交点也是P,则无需计算BC交点。方法为维护
_insp2shapes这个map<CPoint, set<CShape>>数据结构,为交点到经过它的线集的映射。
- 砍平行:依次加入每个平行组,不需计算组内直线交点,只需遍历
- 再依次遍历圆,暴力求焦点。加到
_insp2shapes里 - 函数返回
_insp2shapes.size()即为交点个数。
- 直线两个剪枝方法:
(四)测试设计
按照代码实现的计划,先后实现三部分功能,实现完即测试,测试通过即提交。测试粒度为pipeline中的函数。测试数据和代码均已上传github。
-
test_input: 构造了4个测试数据,测试输入函数inputShapes的功能,下面为其中一个测试样例,解释见注释:
测试覆盖单线、常规、共点、平行
TEST_METHOD(TestMethod4) { // paralile 数据为两组平行线 // 4 // L 0 0 0 1 // L 0 0 1 1 // L 1 0 1 2 // L 1 0 2 1 //直线一般方程ABC答案集 vector<CLine> ans; ans.push_back(CLine(1, -1, 0)); ans.push_back(CLine(1, -1, -1)); ans.push_back(CLine(1, 0, 0)); ans.push_back(CLine(2, 0, -2)); //直线斜率答案集 vector<CSlope> ans_slope; ans_slope.push_back(CSlope(1.0)); ans_slope.push_back(CSlope(true)); ifstream fin("../test/test4.txt");//读测试输入文件 if (!fin) {//确认读入正确 Assert::AreEqual(132, 0); } //测试开始 CIntersect ins; ins.inputShapes(fin); //获取测试目标数据结构 map<CSlope, set<CLine> > k2lines = ins.getK2Lines(); //对比答案 Assert::AreEqual((int)k2lines.size(), 2); int i = 0; int j = 0; for (map<CSlope, set<CLine> >::iterator mit = k2lines.begin(); mit != k2lines.end(); ++mit, ++i) { Assert::AreEqual(true, mit->first == ans_slope[i]); Assert::AreEqual((int)(mit->second.size()), 2); set<CLine> lines = mit->second; for (set<CLine>::iterator sit = lines.begin(); sit != lines.end(); ++sit, ++j) { Assert::AreEqual(true, ans[j] == *sit); } } } -
test_line_intersect: 构造4个测试样例,测试两线交点函数
calcShapeInsPoint,代码略测试覆盖单线、常规、共点、平行
-
test_cnt_intersect: 构造11个测试样例,测试总数函数
cntTotalInsPoint,代码示例测试覆盖单线、常规、共点、平行、浮点精度、内外切、三线切于一点、压力测试
TEST_METHOD(TestMethod9) { // 相切测试,含内切、外切、直线两圆三线切于一点 // 6 // C 0 0 10 // C 4 3 5 // C - 5 0 5 // L 2 14 14 - 2 // L 0 0 0 1 // L - 10 0 - 10 1 ifstream fin("../test/test9.txt"); if (!fin) { Assert::AreEqual(132, 0); } CIntersect ins; ins.inputShapes(fin); int cnt = ins.cntTotalInsPoint(); Assert::AreEqual(9, cnt); // 总数为9 }
五、性能改进与消除所有告警
(一) 性能改进
运行VS2017的性能探测器,查看自己代码的性能瓶颈。
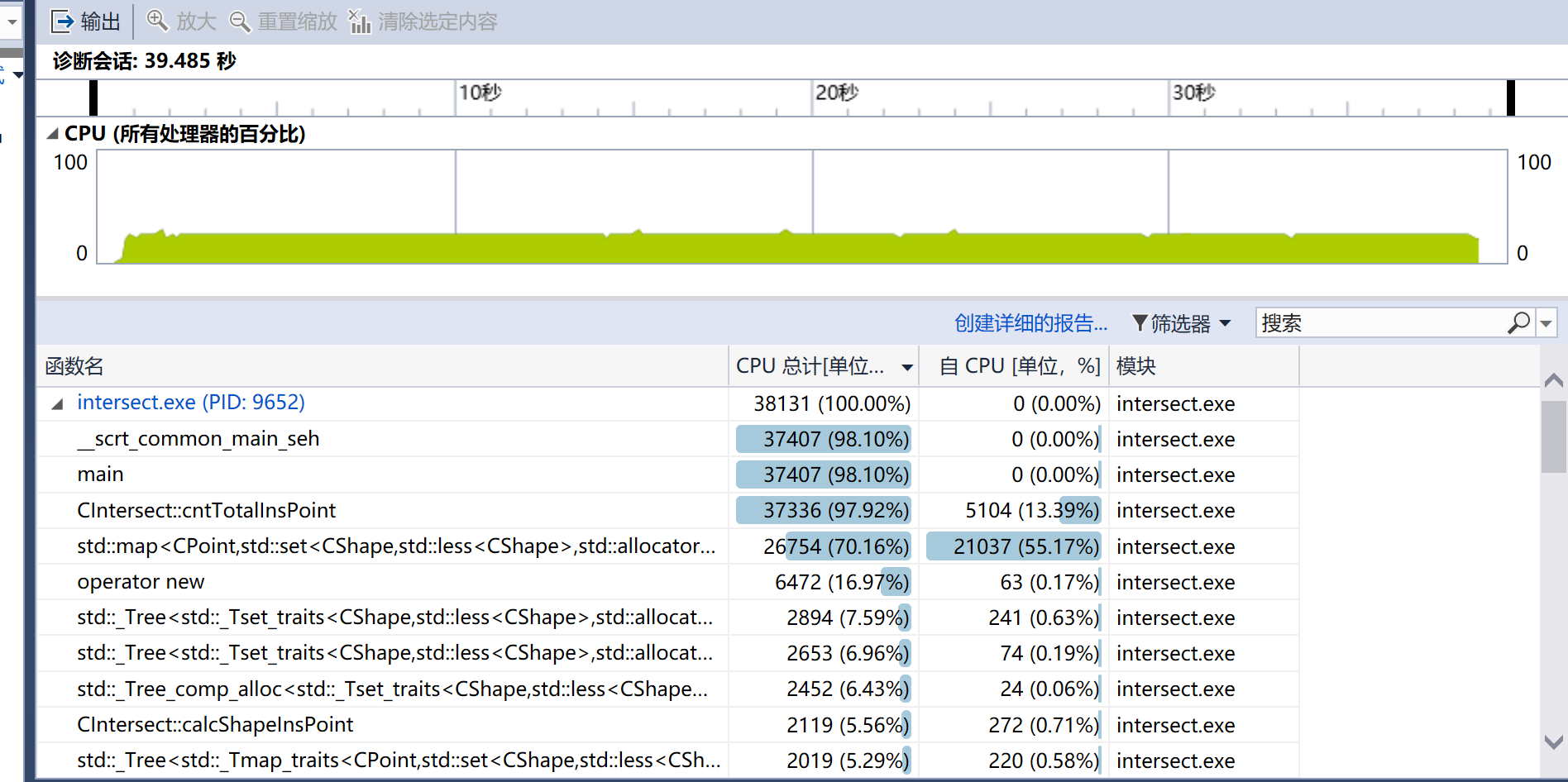
可见运行总耗时38s,最耗时的函数为cntTotalInsPoint, 下面仔细分析此函数,找出性能瓶颈。

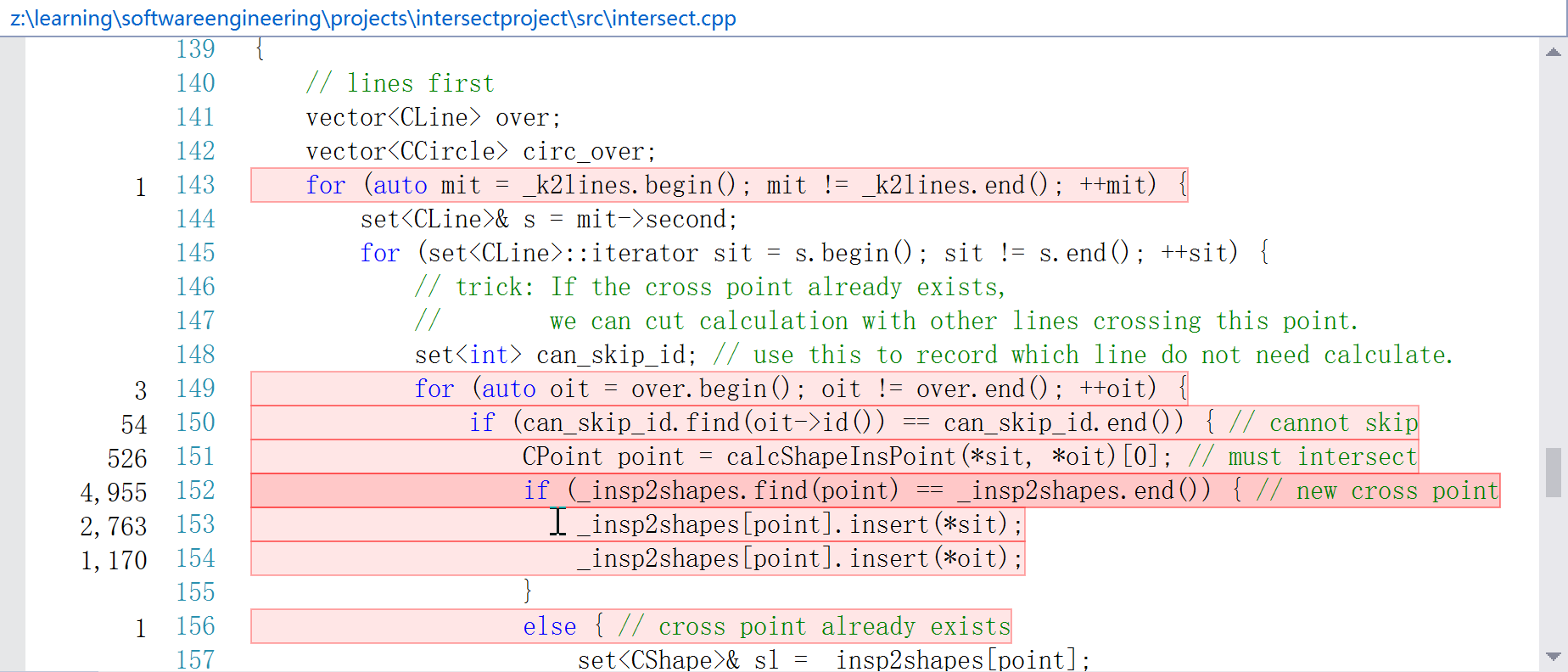
分析:
可见性能瓶颈在map<CPoint, set<CShape>>这个_insp2shapes变量的插入和查找上,通过仔细分析发现,此变量可以优化:
-
由于此变量的作用是通过给定交点,找到通过此交点的线,由于我可以通过id来唯一确定一个CShape,所以直接存int就可以了,
set<CShape>可以改成set<int> -
其次,这个set是不需要查找的,只需要添加,以及整体copy,所以不需要用set,可以改成vector。set在插入前是需要遍历红黑树的,耗时耗内存。于是原来的
map<CPoint, set<CShape>>改成了map<CPoint, vector<int>>。 -
类似的,这个
map<CSlope, set<CLine>>也可以改成map<CSlope, vector<CLine>>。
修改后的性能分析
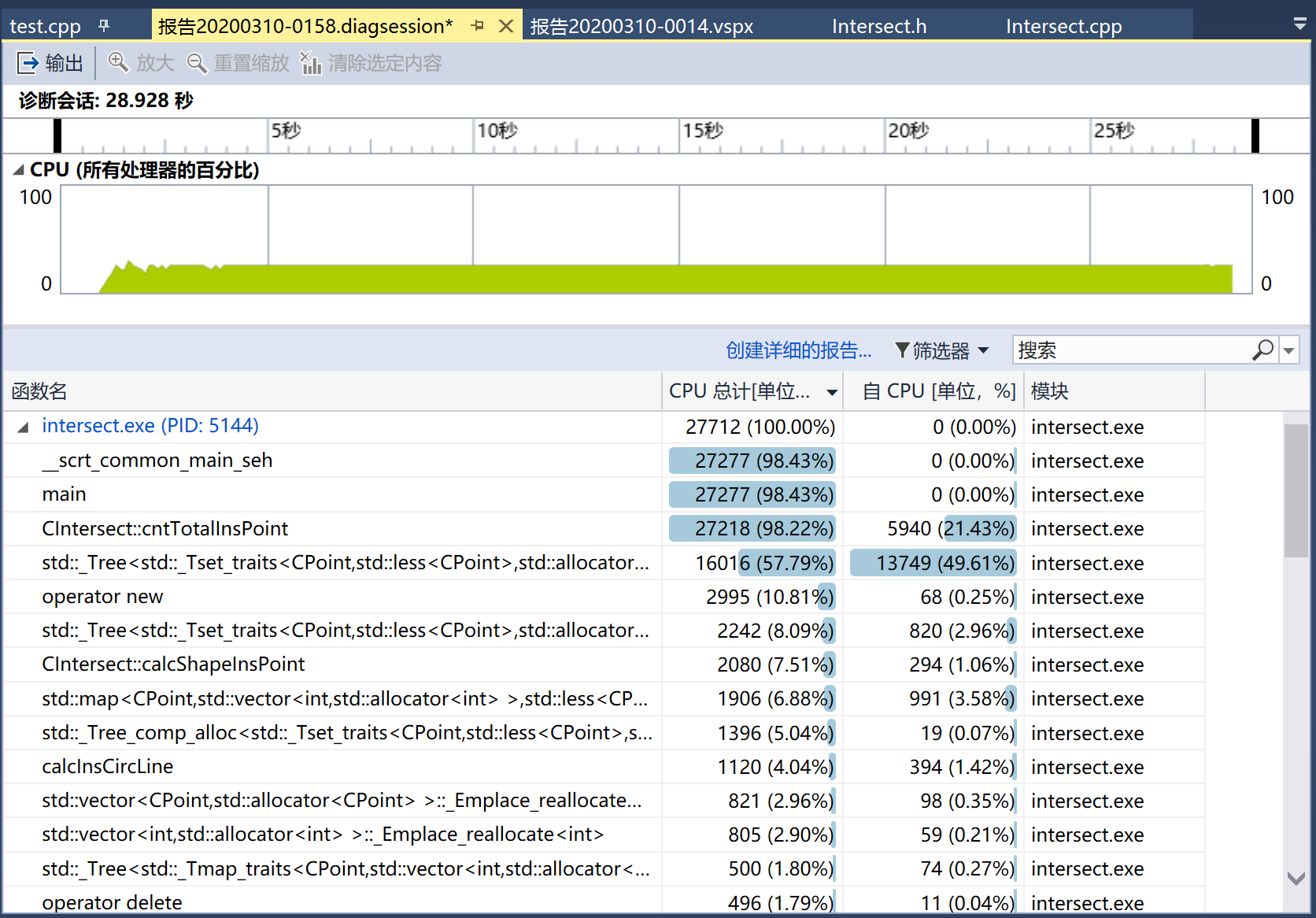
可以看出,运行总时间由38减少到了27,性能大幅度提升。


之前具体的代码被采样到的次数也有所降低,可见修改产生了性能提升。
(二) 消除告警
消除告警前:

消除告警后:
六、代码说明
(一)浮点数比较处理
众所周知计算机中的浮点数是不能直接比较相等的,常见的浮点数相等的比较方法为
#define EPS 1e-6
double x;
double y;
if (abs(x-y) < EPS) {
cout << "x == y" << endl;
}
这种方式保证了在一定的浮点误差内,两个浮点数认为相等。
在本需求中,涉及到若干浮点数相关类需要重载 < 运算符。其代码需要考虑浮点误差问题。例如CPoint类的小于运算符代码如下:
bool CPoint::operator < (const CPoint & rhs) const
{ // 要求仅当 _x < rhs._x - EPS 或 _x < rhs._x + EPS && _y < rhs._y - EPS 时返回true
if (_x < rhs._x - EPS || _x < rhs._x + EPS && _y < rhs._y - EPS) {
return true;
}
return false;
}
(二)求两线交点:直线与直线 or 直线与圆 or 圆与圆
// calculate all intersect points of s1 and s2
// return the points as vector
// need: s1, s2 should be CLine or CCircle.
// special need: if s1, s2 are CLine. They cannot be parallel.
std::vector<CPoint> CIntersect::calcShapeInsPoint(const CShape& s1, const CShape& s2) const
{
if (s1.type() == "Line" && s2.type() == "Line") { // 直线交点公式,输入要求两线不平行
double x = (s2.C()*s1.B() - s1.C()*s2.B()) / (s1.A()*s2.B() - s2.A()*s1.B());
double y = (s2.C()*s1.A() - s1.C()*s2.A()) / (s1.B()*s2.A() - s2.B()*s1.A());
vector<CPoint> ret;
ret.push_back(CPoint(x, y));
return ret;
}
else {
if (s1.type() == "Circle" && s2.type() == "Line") {
return calcInsCircLine(s1, s2);
}
else if (s1.type() == "Line" && s2.type() == "Circle") {
return calcInsCircLine(s2, s1);
}
else { // 两个圆的交点转化为一个圆与公共弦直线的交点
CLine line(s1.D() - s2.D(), s1.E() - s2.E(), s1.F() - s2.F());
return calcInsCircLine(s1, line);
}
}
}
// calculate Intersections of one circ and one line
// need: para1 is CCirc, para2 is CLine
// return a vector of intersections. size can be 0,1,2.
std::vector<CPoint> calcInsCircLine(const CShape& circ, const CShape& line)
{
if (line.k().isInf()) { // 斜率无穷,略
...
}
else if (abs(line.k().val() - 0.0) < EPS) { //斜率为0,略
...
}
else {
vector<CPoint> ret;
double k = line.k().val();
double x0 = circ.x0();
double y0 = circ.y0();
double b1 = line.b().val();
double d_2 = (k * x0 - y0 + b1) * (k * x0 - y0 + b1) / (1 + k * k);
double d = sqrt(d_2); // 圆心到直线距离
double n; // 半弦长
if (d - circ.r() > EPS) { // not intersect
return ret;
}
else if (circ.r() - d < EPS){ // tangent
n = 0.0;
}
else { // intersect
n = sqrt(circ.r() * circ.r() - d_2);
}
double b2 = x0 / k + y0;
double xc = (b2 - b1) / (k + 1 / k); // 弦中点x坐标
double yc = (k * b2 + b1 / k) / (k + 1 / k); // 弦中点y坐标
// 交点坐标
double x1 = xc + n / sqrt(1 + k * k);
double x2 = xc - n / sqrt(1 + k * k);
double y1 = yc + n * k / sqrt(1 + k * k);
double y2 = yc - n * k / sqrt(1 + k * k);
ret.push_back(CPoint(x1, y1));
ret.push_back(CPoint(x2, y2));
return ret;
}
}
(三)平行分组和公共交点剪枝
// the main pipeline: loop the inputs and fill in _insp2shapes or _insPoints
// return the total count of intersect points
// need: _k2lines and _circles have been filled
int CIntersect::cntTotalInsPoint()
{
// lines first
vector<CLine> over;
for (auto mit = _k2lines.begin(); mit != _k2lines.end(); ++mit) { // 遍历平行组
vector<CLine>& s = mit->second;
for (auto sit = s.begin(); sit != s.end(); ++sit) { //遍历组内直线
// trick: If the cross point already exists,
// we can cut calculation with other lines crossing this point.
set<int> can_skip_id; // use this to record which line do not need calculate.
for (auto oit = over.begin(); oit != over.end(); ++oit) { // 遍历over集
if (can_skip_id.find(oit->id()) == can_skip_id.end()) { // cannot skip
CPoint point = calcShapeInsPoint(*sit, *oit)[0]; // must intersect // 能保证不平行
if (_insp2shapesId.find(point) == _insp2shapesId.end()) { // 全新交点
_insp2shapesId[point].push_back(sit->id());
_insp2shapesId[point].push_back(oit->id());
}
else { // cross point already exists 交点已存在
vector<int>& sl = _insp2shapesId[point];
can_skip_id.insert(sl.begin(), sl.end()); // 下次遇到可以跳过不算
_insp2shapesId[point].push_back(sit->id());
}
}
}
}
over.insert(over.end(), s.begin(), s.end());// 整个平行组加入over集
}
// 后面算圆略
...
}
七、思考
-
c++不允许将父类强转为子类,如何更优雅地解决calcShapeInsPoint函数中接收参数是父类类型,但是需要根据不同子类类型使用不同方法的问呢?
std::vector<CPoint> calcInsCircLine(const CShape& circ, const CShape& line)我希望通过这一个函数,封装全部三类的相交问题,所以在接收的参数上必须采用基类的类型,但函数内部计算时需要使用子类的方法,如何实现呢?
- 通过传指针能做到,把参数设为父类的指针,然后强转为子类的指针,但是不太方便,也不太优雅。
- 通过传引用也能实现,利用虚函数的多态特性动态调用对应的子类的函数。但需要在基类里写完全用不到的方法,失去了封装性。如在CShape类里写getA()(目前采用的实现方式)
-
本次使用了c++STL的map和set,底层都是用红黑树实现的,复杂度为O(n)。在讨论交流中发现,c++11标准也新增了类似java中HashSet和HashMap的STL函数,即unordered_map和unordered_set。这个复杂度在好的情况下是O(1)的。下次要记得使用。


