面向对象第一单元总结
面向对象第一单元总结
一、综述
第一单元的主题是求导,共三次进阶性作业
- 第一次:简单多项式求导
- 第二次:带简单正余弦函数且带乘积项的求导
- 第三次:带嵌套函数的求导
在本单元的学习中,我们首先熟悉了java语言的基础语法,然后学习了面向对象程序设计的基本思想,并以代码的形式在作业中实现,包括类,继承派生,多态,基类,接口等等。下面结合UML图对每一次作业进行分析。
二、基于度量来分析自己的程序结构
第一次作业
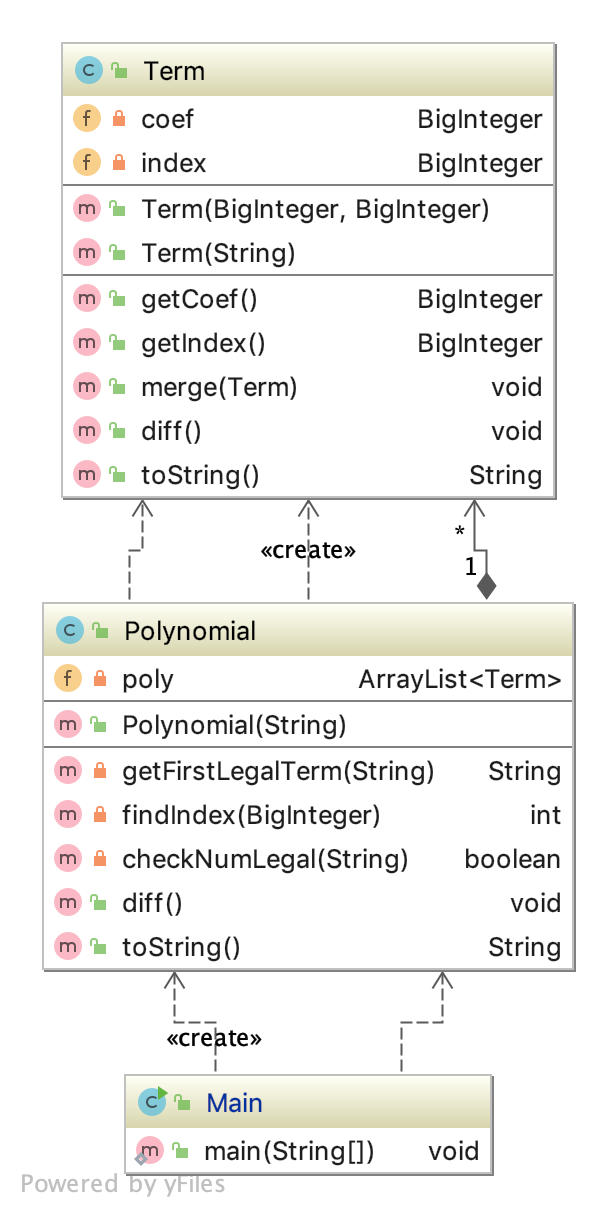
第一次作业要计算一个简单多项式的导数,通过面向对象的抽象原则,我首先抽象出一个Polynomial类,存储一个多项式,由于多项式的求导都是基于项的求导,所以自然需要抽象出Term类。于是第一次作业就呈现了下图所示的结构,Main类是程序的入口。
功能实现
Poly类维护一个ArrayList存放各个Term,Term类维护一个系数Coef和一个指数Index域,表示一个项\(Coef\cdot x^{index}\)。求导时,调用Poly类的diff方法,其将遍历ArrayList中的每一个Term,调用Term类的diff方法,Term类的diff按照单项式的求导公式计算,实现多项式的求导。
性能优化
本次优化很简单,主要考虑合并同类项以及首项非负两个问题。对于合并同类项的操作,我在Poly类的构造函数中实现,目的是让每一个Poly只要构造出来就是最简形式。实现方法为,每加入一个Term之前,先查看List中是否有其同类项,若有则合并,并检查合并后系数是否为0,如果为0则删掉此Term,若未找到同类项则插入Term。对于首项非负,在toString函数中实现,找到第一个首项非负的项,让其与首项交换位置。通过此方法得到了100分的性能分。
自我评价
本次作业的架构较好之处在于其结构非常简单,十分易于实现。缺点是其可扩展性和安全性不强,其中的diff函数都是直接修改私有属性,这让两个类都成为了可变类,极不利于程序的扩展。好在本次作业中不需要对象拷贝等操作,所以这个问题在安全性上没有暴露出问题。最后放出代码的复杂度分析,可见其复杂度还是比较低的。


第二次作业
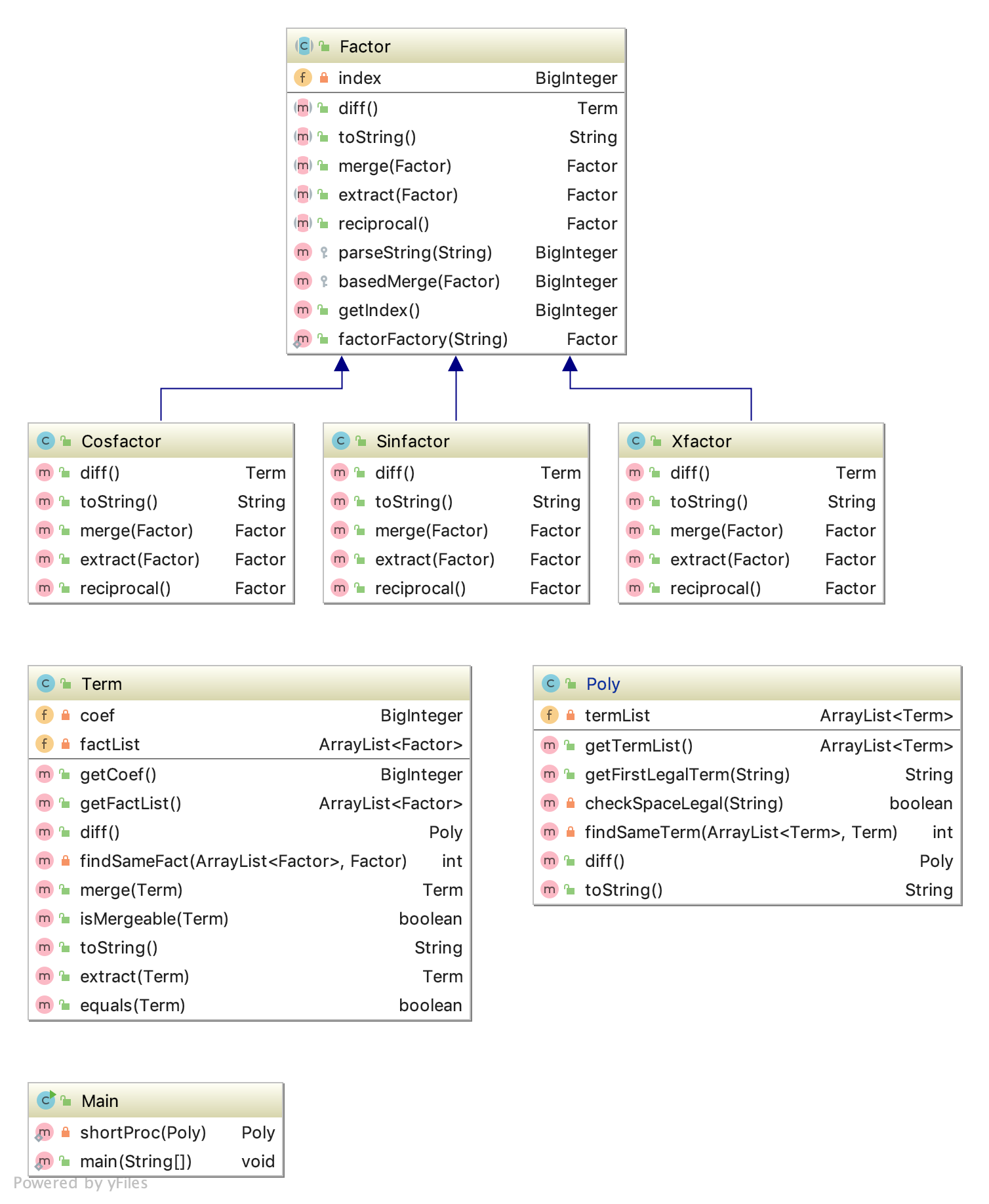
第二次作业在第一次作业的基础上增加了两个变化,首先是sin/cos函数的引入,第二是允许乘积项。考虑到第一次作业的不可扩展性,我选择了重构。本次重构我严格采用扩展性优先的原则,放弃了四个参数莽的无脑做法,对下一次作业可能的需求进行认真分析,最终采用了以下结构。Poly类建模整个表达式,Term类建模一个乘积式,Factor类是一个抽象基类,Xfactor,Sinfactor,Cosfactor继承自Factor类建模各个因子。
功能实现
Poly类维护一个ArrayList存放各个Term,Term类维护一个系数Coef和一个Factor的ArrayList域,表示一个项\(Coef\cdot F_1 \cdot F_2 \cdots\)。求导时,调用Poly类的diff方法,其将遍历ArrayList中的每一个Term,调用Term类的diff方法,Term类的diff按照乘积函数求导公式进行计算,调用Factor类的diff函数,最终实现多项式的求导。
性能优化
本次优化比较复杂,尤其是某个狠人想到\(sin^2(x)+cos^2(x)=1\),类似的很多公式,使得本次作业很难化到绝对最简,我主要考虑了以下几种类型的化简,最终取得了100分的性能分。
-
合并同类项
本次作业合并同类项的想法基于第一次,直接在构造函数中实现,保证每个对象构造出来之后一定最简。区别是,本次要实现两种类的合并同类项,Term类需要合并相同的Factor,Poly类需要合并相同的Term。因为时间复杂度不在作业的性能考量之内,采用的算法为暴力地循环遍历。
-
基于三角函数公式的化简
-
\(aFsin^2(x)+bFcos^2(x)\) 化简为 \(aF+(b-a)Fcos^2(x)\)
-
\(aF+bFcos^2(x)\) 与 \((a+b)F-bFsin^2(x)\) 的互相转换
-
\(Fsin^4(x) - Fcos^4(x)\) 转换为 \(Fsin^2(x) - Fcos^2(x)\)
这三种化简的实现方式大体相同,其核心在于找到两项之间相同的公因式F,以第一个公式为例,我的做法是用两个ArrayList分别存储每个Term提取\(sin^2(x)\)和\(cos^2(x)\)后的项,然后两重循环遍历这两个ArrayList查找有无相同因子F。虽然时间复杂度略高,但是处理本次作业的多项式仍然绰绰有余。
-
-
首项非负
采用和上一次作业相同的方式,在toString函数中处理。在此不再赘述。
自我评价
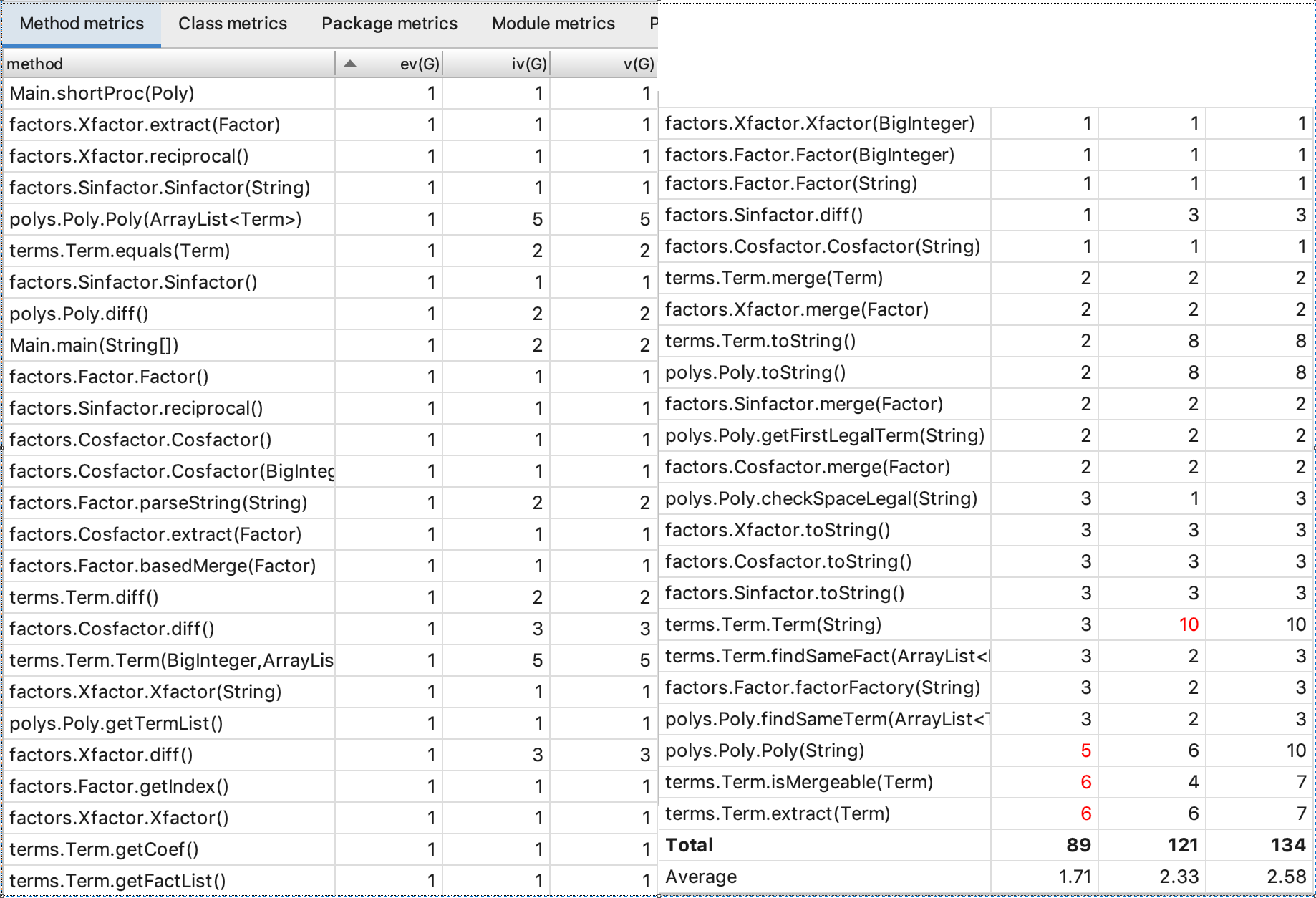
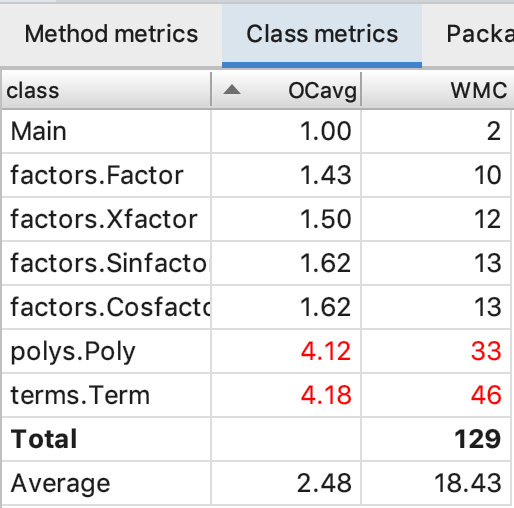
本次作业的架构充分考虑了下一次作业的各种扩展可能,个人认为结构比较好。用Factor抽象基类实现让各个因子类拥有相同的方法接口,使得Term的构造和求导都可以利用动态绑定机制实现调用正确因子的相关方法,不需要人为特判类型,降低了代码复杂度。Factor继承链的构造采用工厂模式,在Factor基类中实现了静态工厂方法来生成每一种Factor子类,对Term类实现Factor其它子类的隐藏,形成良好的封装结构。不足之处在于化简部分的代码完全按照面向过程的思维和结构进行组织,可扩展性非常差,在第三次的代码中,这部分化简完全被抛弃了。下面是代码复杂度。
第三次作业
第三次作业在第二次的基础上增加了嵌套因子和多项式因子两种类型,其复杂程度以几何量级增加,想要满足正确性都有些困难,好在上次进行了精心的架构,这次基本在上次基础上进行扩展。由于多项式因子的引入,万物皆因子,我定义了一个BaseFactor抽象基类,将Poly、Term以及上次的基类Factor都继承BaseFactor,由此达到共享相同方法接口的目的,Term维护的ArrayList中存放的类型变为BaseFactor。对于嵌套因子,本次作业特指sin和cos函数可以嵌套因子,故在原Sinfactor和Cosfactor类中加入BaseFactor域,实现嵌套因子。类关系图如下。
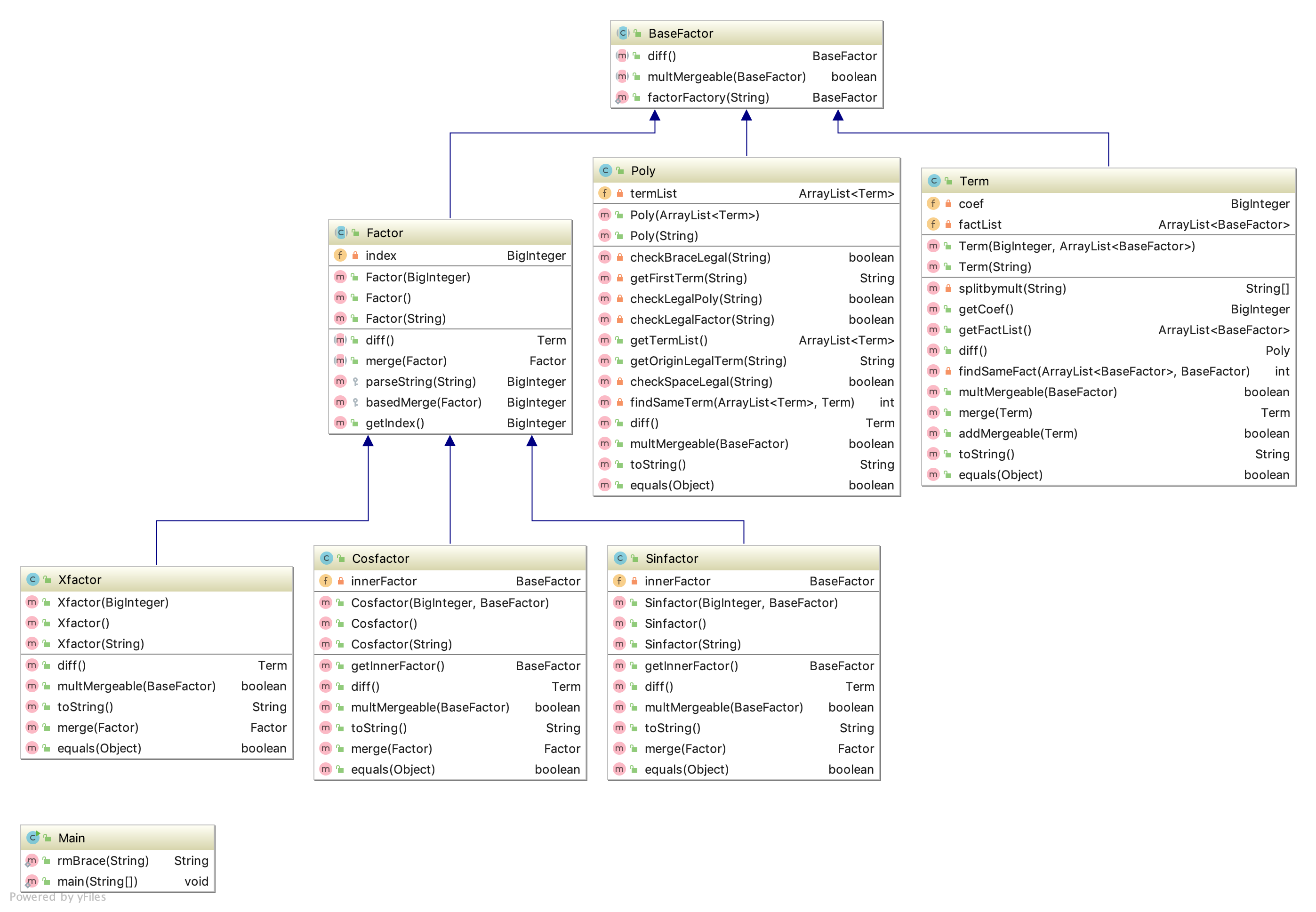
功能实现
本次作业功能是难点,主要体现在两个方面,计算图的构建(输入部分)和求导功能的实现。
-
计算图的构建
计算图的构建即将输入的表达式字符串转化为我们定义的各种类,由于有了嵌套因子和多项式因子,我们很难像前两次作业一样使用正则表达式直接进行语法检查或将多项式拆分成项,由于java正则表达式本身不支持递归嵌套功能,所以我采用递归函数的方法实现语法检查,并将多项式拆分。
-
求导功能实现
BaseFactor中定义抽象diff方法,所以每个子类都必须实现diff方法,整个求导过程与第二次作业完全相同,这也体现了第二次作业架构的正确性,我只重写了Sinfactor和Cosfactor两个类的求导方法,因为其变成了嵌套因子,需要采用链式求导法则。通过diff方法的自动递归调用,我们将所有类的求导都最终转化为了普通因子\(x\),\(sin(x)\),\(cos(x)\) 的求导问题。
性能优化
对本次作业的优化,我将重心放在了去括号与合并同类项上,时间原因并未处理上次那种三角函数公式的化简,所以性能分没得满分。在此重点分享一下去括号的思想。
-
去括号
所谓去括号,并非真的去(括号),括号只是在你输出的时候才会有的,在计算图中并没有括号这个概念。那神马玩意输出时会产生括号呢?当然是Poly类的对象了。例如有一个最简单的因子\(x\),独自构成一个Term,之后这个Term独自构成Poly,这个Poly又被嵌套在一个sin中,就会输出\(sin((x))\)的结构,这就是括号变多的原因。类似地我们还可能输出\((x)+(x)\)这种东西,明明是可以利用前两次的合并方法合并成\(2*x\)的。
知道了产生原因,解决方案自然就可以想到了,那就是“降级”。什么意思呢?就是如果某Poly只包含一个Term,它就可以降级成Term;如果一个Term只包含一个BaseFactor,它就可以降级成一个BaseFactor。利用这个原理,上例中的\((x)\) 是一个Poly,可以降级成\(x\) (Term),继续降级成\(x\) (Xfactor)。这样就可以实现去括号了。
-
合并同类项
这次的合并同类项比之前的作业多了一个trick。因为一切都是因子,使得Term中可能含有Term,这就耽误了Term的合并同类项,所以我们应该把内层的Term拆开,将其中包含的因子放入外层的Term。同理Poly也存在这个问题,只不过更加隐蔽,你可能会看到这种输出\((x+1)+1\),为什么会多一个括号,而且导致两个常数不能合并了呢?原因在于Poly中存的\((x+1)\)这个Term仅有一个因子而且还是个Poly。这实际上可以看成Poly中有Poly,可以利用上述相同的思想,将内层的Poly展开,将其中的Term放入外层的Poly,就能实现将\((x+1)+1\)化简为\(x+2\)了。
自我评价
本次作业在架构上扩展于上一次作业,让我体会到了利用面向对象的思想进行架构的优势。这次的继承体系更加复杂,一开始觉得将Poly类继承自BaseFactor有些循环定义的感觉,但实际上由于java万物皆指针,可以把这种结构理解为C语言中的自引用结构。而且字符串是有限长的,最后的递归终点肯定会到达基本因子。这次的缺点在于上次的三角函数化简不是用面向对象的方法写的,所以这次无法复用,导致性能分未满,有些可惜。这次的代码复杂度还是很可怕的,在处理去括号与合并等问题时全部归到构造函数中了,看来不是一个好的设计模式。


三、分析自己程序的bug
很遗憾,这三次作业无论是强测还是互测都并未被发现bug。我觉得想要让自己不被挑出bug,关键在于自己做到全面的测试,关于测试我就直接在下一段介绍。
四、如何找到自己/别人的bug
如何做好测试呢,我主要分两个方面进行测试,单元测试和整体测试。
单元测试
鉴于这三次作业我们对规格没有要求,所以几乎很难对别人的代码进行单元测试,不过对自己的代码进行单元测试可以把bug扼杀在摇篮中,以免到最后结构复杂时无法定位bug来源。
我采取的方式是一边写一边测,写一个类测一个类,按照自底向上的顺序写类,比如在第二次作业中,先写各个Factor类,写完一个就可以测试一个,保证其各个public接口都符合预期。之后写完Term可以将Factor和Term一起测试,最后写完Poly就可以进行整体测试了。
整体测试
整体测试是测试中最关键的,因为各个零部件都是好的,合在一起也可能出问题。我主要使用两个手段进行整体测试,测评脚本和边缘数据。
-
测评脚本
这种测试方法主要测试功能的正确性,测评脚本会根据正则表达式自动生成随机数据,通过sympy包进行正确性判定,可以快速测试自己/他人的程序是否存在基本正确性的问题。缺点是其构造的数据较弱,很少构造出杀伤力强的边缘数据。
-
边缘数据
这种数据基本只能靠人力思考,通过一次次地阅读实验指导书,可以尽可能多地发现各种边缘数据,这种方法一个人的力量往往太过渺小。我们采用多人研讨的方式,将自己认为边缘的数据分享出来,找到了很多自己意识不到的bug。同时,将这些数据搜集起来测试别人的代码往往能得到大丰收。
关于定向爆破
是否结合被测程序的代码设计结构来设计测试用例?这个问题我姑且理解为通过认真阅读对方代码发现bug定向爆破。因为需要阅读的代码数量实在太多了,我做不到认真阅读每一份代码,而是采取了阅读易错部分来实现定向爆破。通过查看每份代码的正则表达式部分,可以很容易地发现其对指导书的错误理解,进而构造出错误数据定向爆破。这种方式还是崩了不少人的hh~。
五、Applying Creational Pattern
从第二次作业开始,我主要使用的模式就是工厂模式,因为整个任务的核心和整个继承体系的核心是因子Factor,而Factor本身是抽象基类,所以可以将Factor这个继承体系用工厂模式管理。
工厂模式的核心是静态工厂方法,我在此贴出第三次作业静态工厂方法的代码:
public static BaseFactor factorFactory(String str) {
if (str.charAt(0) == 's') {
return new Sinfactor(str);
} else if (str.charAt(0) == 'c') {
return new Cosfactor(str);
} else if (str.charAt(0) == '(') {
return new Poly(str.substring(1, str.length() - 1));
} else {
Pattern r = Pattern.compile("[\\+\\-]?\\d+");
Matcher m = r.matcher(str);
if (m.matches()) {
return new Term(m.group(0));
}
return new Xfactor(str);
}
}
有了静态工厂方法,调用者根本不需要知道Factor继承体系中的内部结构,只需要将字符串丢给静态工厂方法,就能自动生产出对应子类的对象,提高了类封装性。


