23.图像金字塔

1、高斯金字塔

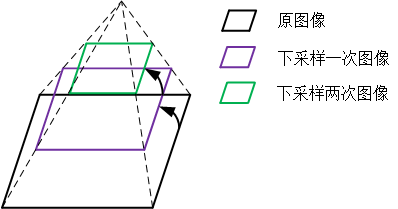
　　构建图像的高斯金字塔是解决尺度不确定性的一种常用方法。高斯金字塔是指通过下采样不断的将图像的尺寸缩小，进而在金字塔中包含多个尺度的图像，高斯金字塔的形式如图3-30所示，一般情况下，高斯金字塔的最底层为图像的原图，每上一层就会通过下采样缩小一次图像的尺寸，通常情况尺寸会缩小为原来的一半，但是如果有特殊需求，缩小的尺寸也可以根据实际情况进行调整。由于每次图像的尺寸都缩小为原来的一半，图像尺缩小的速度非常快，因此常见高斯金字塔的层数为3到6层。OpenCV 4中提供了pyrDown()函数专门用于图像的下采样计算，便于构建图像的高斯金字塔，该函数的函数原型在代码清单3-51中给出。

 

代码清单3-51 pyrDown()函数原型
1.  void cv::pyrDown(InputArray src,
2.                       OutputArray dst,
3.                       const Size & dstsize = Size(),
4.                       int  borderType = BORDER_DEFAULT
5.                      )

• src：输入待下采样的图像。

• dst：输出下采样后的图像，图像尺寸可以指定，但是数据类型和通道数与src相同，

• dstsize：输出图像尺寸，可以缺省。

• borderType：像素边界外推方法的标志，取值范围如表3-5所示

　　该函数用于实现图像模糊并对其进行下采样，默认状态下函数输出的图像的尺寸为输入图像尺寸的一半，但是也可以通过dstsize参数来设置输出图像的大小，需要注意的是无论输出尺寸为多少都应满足式（3.15）中的条件。该函数首先将原图像与内核矩阵进行卷积，内核矩阵如式（3.16）所示，之后通过不使用偶数行和列的方式对图像进行下采样，最终实现尺寸缩小的下采样图像。

2、拉普拉斯金字塔

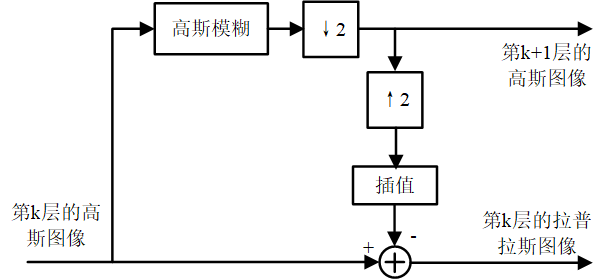
　　拉普拉斯金字塔与高斯金字塔正好相反，高斯金字塔通过底层图像构建上层图像，而拉普拉斯是通过上层小尺寸的图像构建下层大尺寸的图像。拉普拉斯金字塔具有预测残差的作用，需要与高斯金字塔联合一起使用，假设我们已经有一个高斯图像金字塔，对于其中的第i层图像（高斯金字塔最下面为第0层），首先通过下采样得到一尺寸缩小一半的图像，即高斯金字塔中的第i+1层或者不在高斯金字塔中，之后对这张图像再进行上采样，将图像尺寸恢复到第i层图像的大小，最后求取高斯金字塔第i层图像与经过上采样后得到的图像的差值图像，这个差值图像就是拉普拉斯金字塔的第i层图像，整个过程的流程如图3-31所示。

代码清单3-52 pyrUp()函数原型
1. void cv::pyrUp(InputArray src,
2. OutputArray dst,
3. const Size & dstsize = Size(),
4. int borderType = BORDER_DEFAULT
5. )

　　该函数所有参数的含义与pyrDown()函数中相同，使用方式也与其一致，因此这里不再进行赘述。

　　为了了解下采样函数pyrDown()和上采样函数pyrUp()的使用方式，以及高斯金字塔和拉普拉斯金字塔的构建过程，我们在代码清单3-53中给出构建高斯金字塔和拉普拉斯金字塔的示例程序。在例程中我们将原始图像作为高斯金字塔的第0层，之后依次构建高斯金字塔的每一层。完成高斯金字塔的构建之后，我们从上到下取出高斯金字塔中的每一层图像，如果取出的图像是高斯金字塔的最上面一层，则先将其下采样再上采样，之后求取从高斯金字塔中取出的图像与上采样后的图像的差值图像作为拉普拉斯金字塔的最上面一层。如果从高斯金字塔中取出的第i层不是最上面一层，则直接对高斯金字塔中第i+1层图像进行上采样，并计算高斯金字塔第i层图像与上采样结果的差值图像，将差值图像作为拉普拉斯金字塔的第i层。该例程最终的运行结果在图3-32、图3-33中给出。

代码清单3-53 myPyramid.cpp构建高斯金字塔和拉普拉斯金字塔
1.  #include <opencv2\opencv.hpp>
2.  #include <iostream>
3.  
4.  using namespace cv;
5.  using namespace std;
6.  
7.  int main()
8. {
9.    Mat img = imread("lena.png");
10.    if (img.empty())
11.    {
12.      cout << "请确认图像文件名称是否正确" << endl;
13.      return -1;
14.    }
15.  
16.    vector<Mat> Gauss, Lap; //高斯金字塔和拉普拉斯金字塔
17.    int level = 3; //高斯金字塔下采样次数
18.    Gauss.push_back(img); //将原图作为高斯金字塔的第0层
19.    //构建高斯金字塔
20.    for (int i = 0; i < level; i++)
21.    {
22.      Mat gauss;
23.      pyrDown(Gauss[i], gauss); //下采样
24.      Gauss.push_back(gauss);
25.    }
26.    //构建拉普拉斯金字塔
27.    for (int i = Gauss.size() - 1; i > 0; i--)
28.    {
29.      Mat lap, upGauss;
30.      if (i == Gauss.size() - 1) //如果是高斯金字塔中的最上面一层图像
31.      {
32.        Mat down;
33.        pyrDown(Gauss[i], down); //上采样
34.        pyrUp(down, upGauss);
35.        lap = Gauss[i] - upGauss;
36.        Lap.push_back(lap);
37.      }
38.      pyrUp(Gauss[i], upGauss);
39.      lap = Gauss[i - 1] - upGauss;
40.      Lap.push_back(lap);
41.    }
42.    //查看两个金字塔中的图像
43.    for (int i = 0; i < Gauss.size(); i++)
44.    {
45.      string name = to_string(i);
46.      imshow("G" + name, Gauss[i]);
47.      imshow("L" + name, Lap[i]);
48.    }
49.    waitKey(0);
50.    return 0;
51.  }