第五章小结

学会了树和二叉树的定义，以及树的基本术语

二叉树的链表存储表示：

typedef struct BiTNode{
     TElemType data;
     struct BiTNode *lchild, *rchild;    
}BiTNode, *BiTree;

学会了先序（根->左->右），中序（左->根->右），后序（左->右->根）以及层次(自上而下，从左到右) 相应代码如下：

void InOrderTraverse(BiTree T){//中序遍历 
    if(T)//如果T非空 
    {
        InOrderTraverse(T->lchild);
        cout<<T->data;//左根右的顺序输出 
        InOrderTravese(T->rchild);
    }
}

void PreOrderTraverse(BiTree T){//先序遍历 
    if(T)//如果T非空 
    {
        cout<<T->data;//根左右的顺序输出 
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}

void AfterTraverse(BiTree T){//后序遍历 
    if(T)//如果T非空 
    {
        AfterTraverse(T->lchild);
        AfterTraverse(T->rchild);
        cout<<T->data;//左右根的顺序输出 
    }
}

了解到有一种叫二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树），是左孩子小于根，根小于右孩子

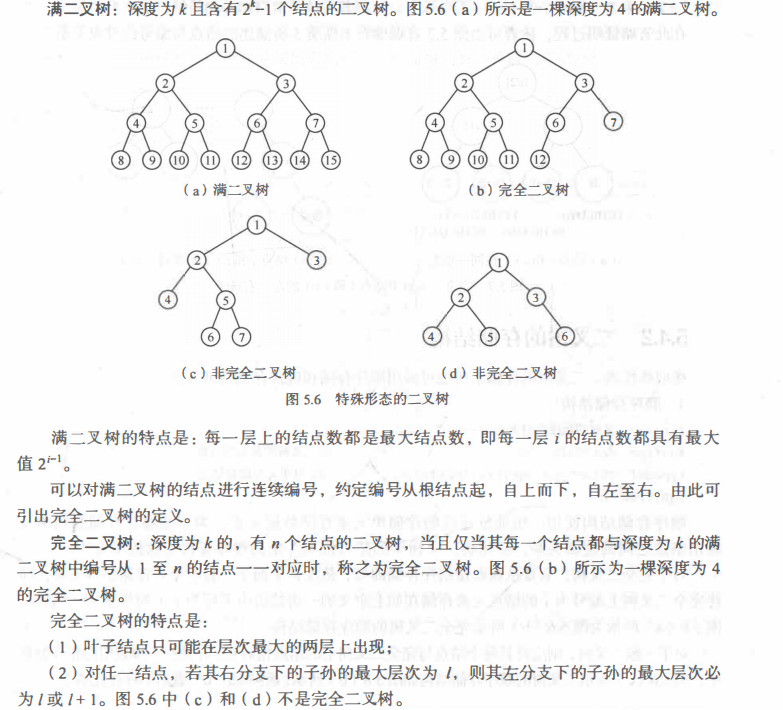
还有满二叉树，完全二叉树:

 

 

二叉树三个性质：

1.第i层最多有2^(i-1)个结点

2.深度为k的二叉树最多有2^k - 1个结点

3.设度为0的结点数为N0， 1为N1， 2为N2， 则N0 = N2 +1

结点总数N = N0+ N1 +  N2 = N1 + 2*N2 +1

 

树的存储结构：

1.双亲表示法（由下而上）

2.孩子表示法（由上而下）

3.孩子兄弟法：又称二叉树表示法，或二叉链表表示法，即以二叉链表做树的存储结构。链表中结点的两个链域分别指向该结点的第一个孩子结点和下一个兄弟结点，分别命名为 firstchild 域和 nextsibling域

II- - - - - -树的二叉链表（孩子－兄弟）存储表示－－－－－

typedef struct CSNode{

ElemType data;

struct CSNode *firstchild, *nextsibling;

) CSNode,*CSTree;

 

 

森林和二叉树的转换：

　　左孩子右兄弟

 

 

 

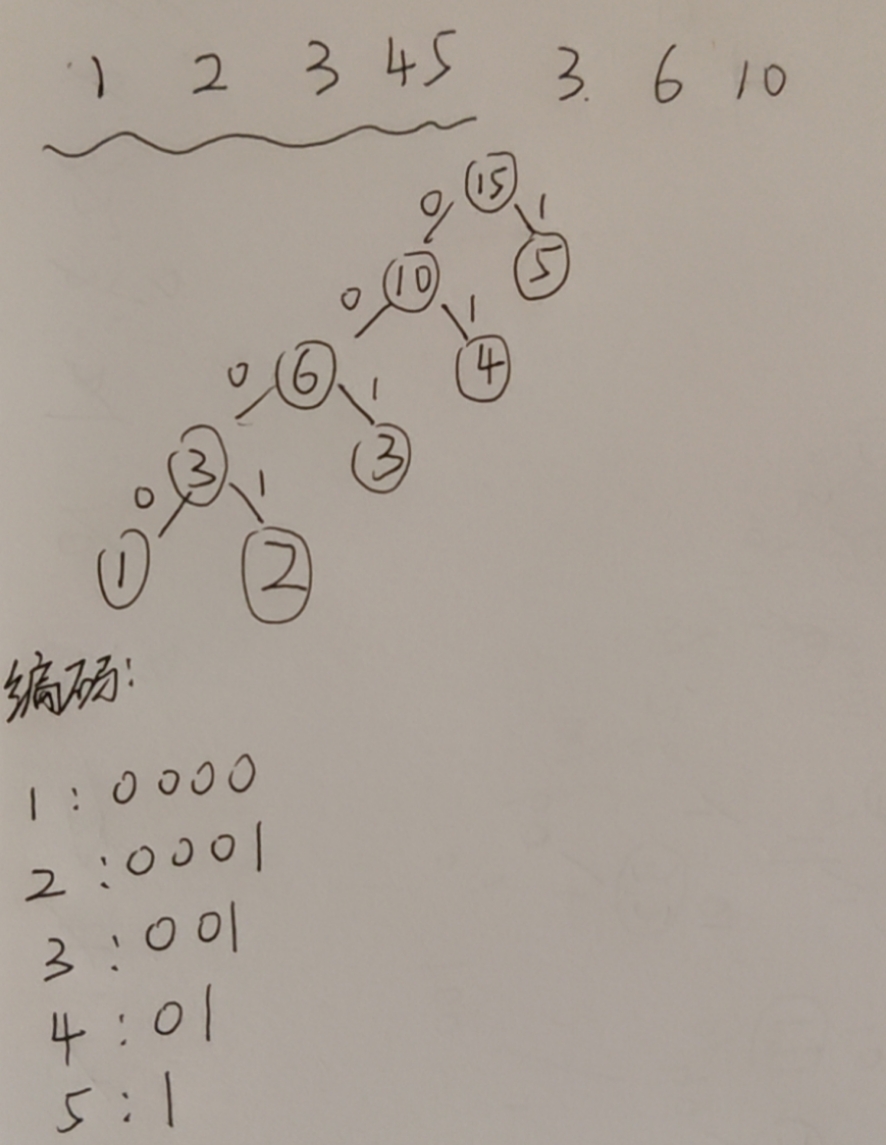
 哈夫曼树：

没有最优哈夫曼树，哈夫曼树一定是最优二叉树，最优二叉树的带权路径长度（WPL）一定等于哈夫曼树构建出来的WPL；

构建方法：不断选取最小的两个，已经被选的两个的根也在选择范围内，选出作为孩子，不断地往上构建

 

 

如上图构建出来最后的哈夫曼树WPL为：2*3+4*3+5*2+7=35 

 

哈夫曼编码：

性质1 哈夫曼编码是前缀编码。 

性质2 哈夫曼编码是最优前缀编码。 

约定为左0右1

如下图