AGC017

C Snuke and Spells

对于每个值 \(i\)，假设有 \(x\) 个 \(i\)，就覆盖 \([i-x+1,i]\)，那么答案就是没被覆盖的点的个数。

D Game on Tree

对于一个状态，定义 \(x\) 的一个转移表示删掉 \(x\) 子树内的一个子树。

如果 \(x\) 只有一个儿子，则 \(x\) 的 \(SG\) 值等于儿子的 \(SG\) 值 \(+1\)。（显然 \(x\) 能转移到儿子的每一个状态以及删儿子的状态）

对于多个儿子，由于不同子树内的操作互不影响，所以可以看成多个独立的游戏，而每个游戏都分别加上了到父亲的一条边，所以类似一个儿子的情况 \(SG\) 要加一。

也就是 \(SG_x=\bigoplus(SG_v+1)\)

E Jigsaw

把接口看作点，拼图看作边，考虑构造一下接口的点权使得权值相同的点刚好能够接起来。

构造权值也很简单，左边接地则为 \(a_i\)，否则为 \(-c_i\)；右边接地为 \(-bi\)，否则为 \(di\)。

这样对接口赋值以后权值相同的两个点刚好能接起来，而且不会左接左或者右接右。

问题变为一个图里找若干条路径，要求起点正，终点负，等价于正点出度大于等于入度，负点相反。

注意特判一种特殊情况，即连成一个环，此时图是满足上述条件的，但是根据实际意义显然不能这样连，所以对每个弱连通分量判断一下是否每个连通块包含一个入度不等于出度的点。

F Zigzag

有一个很显然的 dp，设 \(f[i][S]\) 表示第 \(i\) 条线状态为 \(S\)，暴力枚举转移，复杂度为 \(O(2^n2^npoly(nm))\)。

实际上可以沿用轮廓线dp的思想，对每条线从上到下一步一步转移。
假设当前在 \(j\) 层，那么 \(S\) 前 \(j\) 位表示当前线，后面的几位表示上一条线的走法，但是想要精确知道上一条线当前在哪个点的话，还要记录一下两条线在这一层的距离。
这样复杂度降到了 \(O(2^nn^2m)\)，考虑到状态、当前线和当前层这几维想要优化掉很难，所以从优化两条线之间的距离入手。

现在的问题变为，如果我们只知道当前这条线前 \(j\) 层是怎么走的，如何判断上一条线和这一条线是否相交。

注意到一个性质，如果在某一时刻上一条线往左走（蓝），这一条线往右走（红），即这样一种情况：

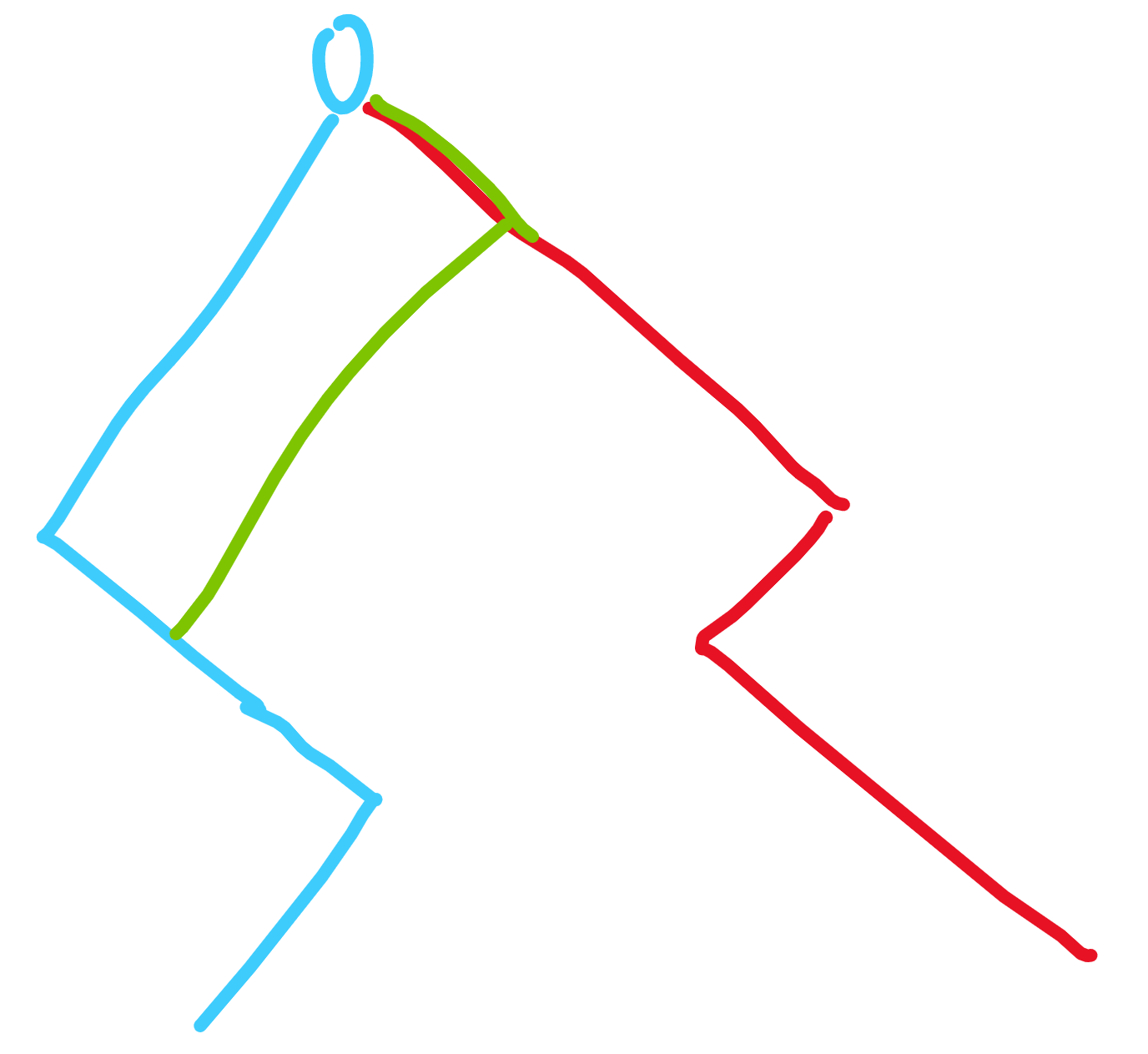
假设最坏的情况，红线此后一直往左走（也就是绿色情况），那么直到蓝绿相交前这一段，是不可能和红线相交的，所以我们就想到可以把蓝线这一段强行扭成绿线。

具体来讲就是找到蓝色的下一次“往右”操作，然后挪动到这一步来。

这样做的好处在于，把蓝线调整了以后，直到当前层每一步蓝线和红线都是一样的，而且蓝红线的相交状况和调整前是一摸一样的，就不用记录上一条线当前层在哪个点了。