[AGC019F] Yes or No

tag:组合计数

---

题意

有 \(n\) 个回答yes的问题和 \(m\) 个回答no的问题，求最优策略下期望回答正确的答案个数，回答一个问题后立刻可以知道是否回答正确。

\(n,m\leq5\cdot10^5,\ mod=998244353\)

---

首先我很naive地认为最优策略是乱回答

最优策略是：假设当前还剩了 \(a\) 个yes问题和 \(b\) 个no问题

• \(a<b\) 回答yes
• \(a\ge b\) 回答no

显然这样回答正确的概率是最高的

---

可以抽象出一个问题，从 \((n,m)\) 走到 \((0,0)\)，每一步只能往左/下。于是根据最优策略，我们可以确定在每个点，下一步会走向的位置。

（从粉兔那儿贺了一张图）

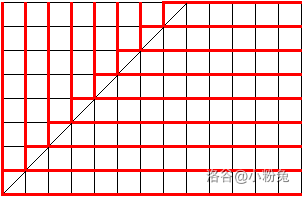
然后每一种问题组合就刚好对应着一条从 \((n,m)\) 到 \((0,0)\) 的路径，所以问题变为每一条路径经过的红色线段数量和，除以路径条数。

对于这种网格图路径和经过斜线问题，一般想到翻折。对于一条经过斜线的路经，把在斜线上方的部分翻折下来，发现经过的线段数会减少（路径与斜线的交点个数-1）；巧妙的是，对于任意路径，这样翻折以后会经过的线段数都是 \(n\)。

---

所以 \(ans=n+E(\)交点个数\()-E(\)经过斜线的路径数\()\)，可以枚举每一个交点计算贡献。

\[ans=n+\dfrac{\sum_{i=0}^{\min\{n,m\}}\binom{2i}{i}\binom{n-i+m-i}{n-i}-\binom{n+m}{n}}{\binom{n+m}n} \]

#include<bits/stdc++.h>
using namespace std;

template<typename T>
inline void Read(T &n){
	char ch; bool flag=0;
	while(!isdigit(ch=getchar()))if(ch=='-')flag=1;
	for(n=ch^48;isdigit(ch=getchar());n=((n<<1)+(n<<3)+(ch^48))%998244353);
	if(flag)n=-n;
}

enum{
    MAXN = 500005,
    MOD = 998244353,
    inv2 = MOD+1>>1
};

int n, m;
int jc[MAXN<<1], invjc[MAXN<<1];

inline int ksm(int base, int k=MOD-2){
    int res=1;
    while(k){
        if(k&1)
            res = 1ll*res*base%MOD;
        base = 1ll*base*base%MOD;
        k >>= 1;
    }
    return res;
}

inline void prework(int n){
    jc[0] = 1; for(register int i=1; i<=n; i++) jc[i] = 1ll*jc[i-1]*i%MOD;
    invjc[n] = ksm(jc[n]); for(register int i=n; i; i--) invjc[i-1] = 1ll*invjc[i]*i%MOD;
}

inline int C(int n, int m){return 1ll*jc[n]*invjc[m]%MOD*invjc[n-m]%MOD;}

inline int dec(int a, int b){
    a -= b;
    if(a<0) a += MOD;
    return a;
}

int ans=0;

int main(){
    Read(n); Read(m);
    prework(n+m);
    for(register int i=0; i<=n and i<=m; i++)
        ans = (ans+1ll*C(i+i,i)*C(n-i+m-i,n-i))%MOD;
    ans = dec(ans,C(n+m,n));
    printf("%lld\n",(max(n,m)+1ll*inv2*ans%MOD*ksm(C(n+m,n)))%MOD);
    return 0;
}