CF1694E Keshi in Search of AmShZ#800(div.2)
题目链接
https://codeforces.com/contest/1694/problem/E
题意简述
\(Keshi\) 准备从城市 \(1\) 出发,前往 \(AmShZ\) 所在的城市 \(n\) .这里一共有 \(n\) 个城市 ,编号 \(1 \sim n\),有 \(m\) 条有向道路. \(Keshi\) 不知道城市的路线,他需要听从 \(AmShZ\) 的指挥.
每一天的开始, \(AmShZ\) 告诉 \(Keshi\) 以下两条信息之一
- 告诉他一个阻挡的道路 ,之后 \(Keshi\) 将永远不会走这条道路,并且他会留在他当前所在的城市一天
- 让 \(Keshi\) 开始移动 , \(Keshi\) 将会随机选择一条路线移动到附近的一个可以到达的相邻的城市.如果无路可走,他将留在当前城市
现在告诉你城市和道路的数量,以及各个道路的起始点和终点
请你告诉他们最少需要多少天能保证 \(Keshi\) 一定可以到达 \(AmShZ\) 所在的城市
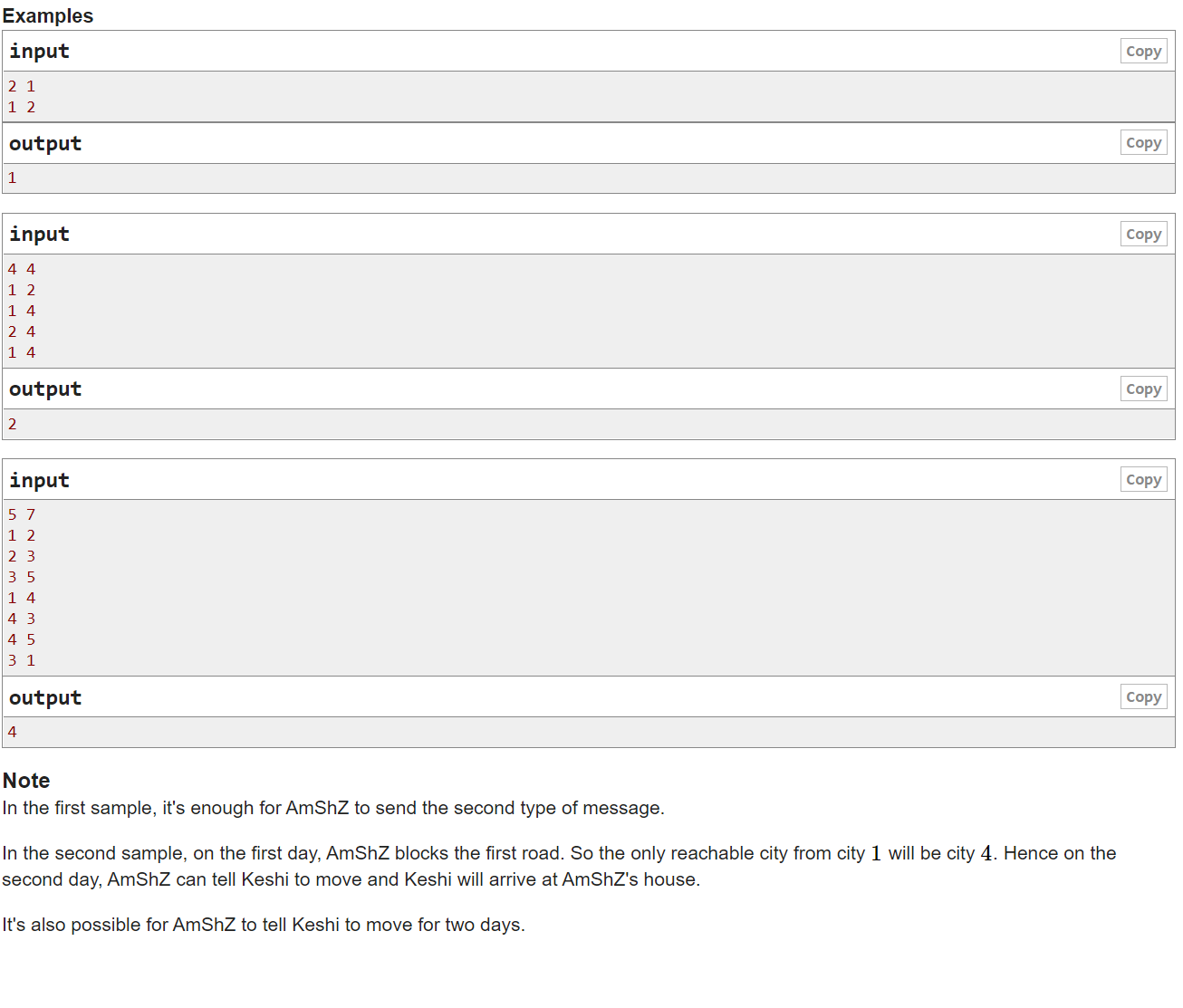
样例
点击查看样例
分析
为了避免引起混淆提前说一下:
一条由 \(a\) \(\rightarrow\) \(b\) 的边,下称 \(a\) 是这条边的起始点 ,\(b\)是这条边的结束点
图中第一次走的起始点称为起点,目的地称为终点.
这个题一开始想的就是从起点开始走,走任何一条边的一次的花费等于这条边的起始点的出度\(-1\) (封堵其他路径的花费)+ \(1\) \((\) 从起始点走到结束点花费一天 \()\).用 \(dist[i]\) 记录 从起点 \(1\) 走到 \(i\) 的最小花费天数,然后愉快的WA16了.
想了很久,搜了很多题解,仍然没想出哪错了..
其实走的过程中有些路径是不用删的,而这种情况是我们从前往后走所无法考虑到(或者说无法判断出)的.
看下面这张图:
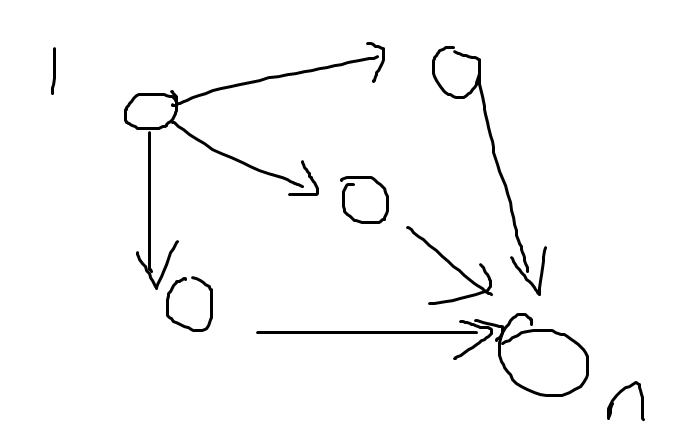
从 \(1\) 到 \(n\) 的距离最小很显然是 \(2\) ,一条边都不用删 .而如果采用我们刚才想的那个删边策略,从 \(1\) 出发走到下一个点 ,无论是哪个,都要删掉两个边,白白的浪费了 \(2\) 天,最后结果是 \(3\) ,比正确答案偏大了.
因此,我们删边的时候还应该考虑到当前边的结束点到结点 \(n\) 的距离长短以确保不会出现浪费次数的情况.也就是我们删边之前需要预先知道将要走过去的这些点到 \(n\) 点的距离.正着走显然是无法解决的.那么我们看看反向建图能不能解决这个问题.
从点 \(n\) 开始往前走 ,每一次取出距离点 \(n\) 最近的点 \(x\) ,用它来更新与 \(x\) 相邻的点到 \(n\) 的距离 .用 \(dis[i]\) 表示点 \(i\) 走到点 \(n\) 最小的无论怎么走一定能走到 \(n\) 的所需花费的天数
考虑下面这种情况
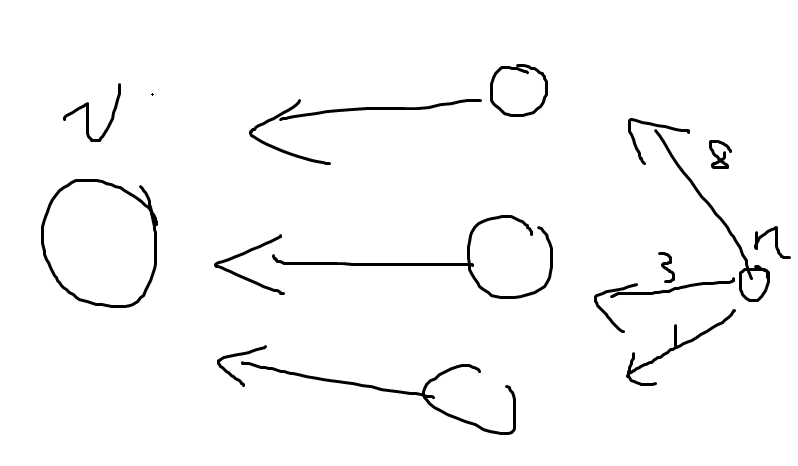
中间这些点到 \(n\) 的距离分别为 $1\ 3\ 8\ $,那么 \(dis[v]\) 就要被这三个点更新
(为了方便起见我们把中间这三个点从下往上编号 \(2\ 3\ 4\))
首先对于 \(dis=1\)的 \(2\) 号点来说, 想用 \(dis[2]\) 来更新 \(dis[v]\) 的话,为了保证 \(v\) 无论怎么走一定能在这个步数内到 \(n\) ,需要把与 \(v\) 相邻的 \(dis\) 比 \(dis[2]\)大的点所连的边删掉. 那么 从 \(2\) 走到 \(v\) 的花费天数就是在 \(2\) 号结点所花费的基础上 ,删掉比 \(2\) 号结点的 \(dis\) 大的点的边,而 \(2\)号点已经是最小的了,也就是删 \(din[v]-1\)条边,\(dist=dis[2]+din[v]-1+1\)(即使从 \(2\) 到 \(v\) 有重边也不会影响答案的正确性,因为我们对重边也会全都遍历到,那么 din[y] 也会随之改变 ,下面会讲到)
对于 \(dis=3\)的 \(3\) 号点来说, 想用 \(dis[3]\) 来更新 \(dis[v]\) 的话,为了保证 \(v\) 无论怎么走一定能在这个步数内到 \(n\) ,需要把与 \(v\) 相邻的 \(dis\) 比 \(dis[2]\)大的点所连的边删掉,即\(3\ 4\) 号点, 那么 从 \(2\) 走到 \(v\) 的花费天数 \(dist=dis[2]+din[v]-2+1\) (结点 \(2\) 的dis更小,不用删结点 \(2\) 的边 ,所以花费天数比 \(2\) 号点少一天)
那么我们如果当前结点能走到 \(v\) 时,由于我们使用了优先队列,显然每次取出的点要么无法到达 \(v\) ,要么是距离 \(v\) 是当前最近的(当然肯定也是未访问过的点),更新完 \(dis[v]\) ,再让 \(dis[v]--\) , 就能保证与 \(v\) 相连的点更新 \(dis[v]\) 时的时间花费是合理的.就直接是\(dis[v]=min(dis[v],dis[u]+din[i])\) 不用额外的减什么东西了.
注意,反图中,在 \(v\) 之前的这些点到 \(n\) 的距离一定是严格小于 \(v\) 到 \(n\) 的距离的 ,所以不会出现还没更新完走到 \(v\) 的这些点时就用 \(v\) 的 \(dis\) 来更新其他点的情况.
代码
点击查看第一次正向建图遍历的错误代码
#include<stdio.h>
#include<iostream>
#include<cstdlib>
#include<string.h>
#include<algorithm>
#include<vector>
#include<unordered_map>
#include<queue>
using namespace std;
typedef long long LL;
const int N=2e5+10;
int e[N],ne[N],idx,h[N];
int dout[N],din[N];
unordered_map<int,int>mp[N];
typedef pair<LL,int>PII;
priority_queue<PII,vector<PII>,greater<PII> > q;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int n,m;
LL dis[N];
int vis[N];
LL dijkstra()
{
memset(dis,0x4f,sizeof dis);
dis[1]=0;
q.push({0,1});
while(q.size())
{
auto t=q.top();
q.pop();
int i=t.second;
if(vis[i])continue;
vis[i]=1;
for(int j=h[i];j!=-1;j=ne[j])
{
int k=e[j];
LL dist=dis[i]+dout[i];
if(mp[i][k]>1)
{
dist-=(mp[i][k]-1);
}
if(dis[k]>dist)
{
dis[k]=dist;
q.push({dis[k],k});
}
}
}
return dis[n];
}
int main()
{
//freopen("uva.txt","r",stdin);
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
if(mp[a].find(b)==mp[a].end())
{
mp[a][b]=1;
add(a,b);
}else mp[a][b]++;
dout[a]++;
}
printf("%lld\n",dijkstra());
return 0;
}
点击查看AC代码
#include<stdio.h>
#include<iostream>
#include<cstdlib>
#include<string.h>
#include<algorithm>
#include<vector>
#include<unordered_map>
#include<queue>
using namespace std;
typedef long long LL;
const int N=2e5+10;
int e[N],ne[N],idx,h[N];
int dout[N],din[N];
unordered_map<int,int>mp[N];
typedef pair<LL,int>PII;
priority_queue<PII,vector<PII>,greater<PII> > q;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int n,m;
LL dis[N];
int vis[N];
LL dijkstra()
{
memset(dis,0x4f,sizeof dis);
dis[n]=0;
q.push({0,n});
while(q.size())
{
auto t=q.top();
q.pop();
int i=t.second;
if(vis[i])continue;
vis[i]=1;
for(int j=h[i];j!=-1;j=ne[j])
{
int k=e[j];
LL dist=dis[i]+din[k];
if(dis[k]>dist)
{
dis[k]=dist;
q.push({dist,k});
}
din[k]--;
}
}
return dis[1];
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
add(b,a);
din[a]++;
}
printf("%lld\n",dijkstra());
return 0;
}

