暑假集训D6 2023.7.29 补题
原比赛链接2022年华中科技大学程序设计新生赛(重现赛)
官方题解 华中科技大学 2022 新生赛(HUST FCPC 2022) 题解&滚榜
\(underset\)
\(\underset{\sim}Λ\)
\(\underset{\sim}{abcd}\)
N.Walk Alone's Conjecture
题意:给定一个整数 \(n\) ,找出两个数 \(x\) 和 \(y\) ,使得满足如下条件
- \(y - x = n\)
- \(x\) 和 \(y\) 的质因子个数相同.(质因子不必相同)
本题特别注意一下数据范围 \(1 \leq n \leq {10}^8\) , \(1 \leq x,y \leq 10^{10}\) .为什么要注意数据范围,后面会提到..
先介绍一下我自己的思路,然后给出官方思路.
首先容易看出,对于一个偶数,必有质因子 \(2\) ,容易得到 \(n\) 和 \(n \times 2\) 即满足题意.
否则如果不是偶数,一定就没有质因子 \(2\) ,如果再没有质因子 \(3\) ,那么 \(n \times 2\) 和 \(n \times 3\) 即为所求.
那如果还有质因子 \(3\) 该怎么办呢?
可以想到,如果再有一个质数 \(a\) , 显然 \(n\times a\) 使得该数多了 \(1\) 个质因子 , \(a+1\) 一定是偶数 ,有质因子 \(2\) ,只要 \(a+1\) 是 \(2\) 的 \(k\) 次幂即可使质因子的个数只增加 \(1\) (做题时没有考虑周全,没有考虑到 \(a+1\) 还包含了其他质因子的情况,把这题想简单了).
那么只需要找一下 \(a\) 满足
- \(a\) 为质数且不为 \(n\) 的质因子
- \(a+1\) 为 \(2\) 的 整数次幂
然后我就满心欢喜写了个程序,发现满足这种情况的质数并不多,由于数据范围所限,并不能乘以一个很大的质数(如 \(2147483647\) ),可惜了不然直接变水题. 好了话说回来,在 \(10^{10}\) 的范围限制下, 只有如下惨淡的几个 \(a\) 和 \(a+1\) 满足上面的条件
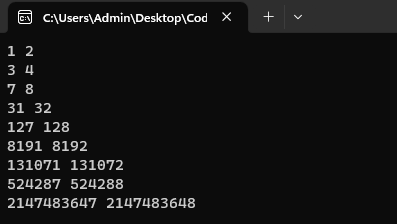
虽然数量惨淡,但是代码还得接着写
int u[7]={3,7,31,127,8191,131071,524287};
for(int i =0;i<7;i++)
{
if(n%u[i]!=0)
{
cout<<n*u[i]<<" "<<n*(u[i]+1)<<endl;
break;
}
}
\(n\) 的量级达到了 \(8\) 次方,再乘以一个大于100的数就超过 \(10\)次方 了..
于是我又想了一招,对那些比较大的数输出一下,然后人工给他构造质因子. 只要使得乘上的乘积的质因子的个数都增大相同的数量即可.
由于我们现在讨论的是没有质因子 \(2\) ,但有质因子 \(3\) 的情况,所以一个数乘以任意个 \(2\) 和 \(3\) 都会使得该数的质因子精确地增加 \(1\) .只用 \(2\) 或 \(3\) 的幂构造出来相差 \(1\) 是比较难的({2,3},{8,9}都满足题意,后面好像就很少了).只用 \(2\) 只能让一个数的质因子增大 \(1\), \(3\) 不能使得该数的质因子变多, 那么不妨再找一个 \(n\) 中没有的质因子,比如 \(7\) ,然后用 \(2,3,7\) 来构造两个数,使得这两个数的差只差 \(1\) 就好了.比如 \(48 = 3*16 = 3*2*2*2*2\),增加1个质因子 \(2\) , \(49 = 7\times 7\) ,增加一个质因子 \(7\) .
最后交上去还是 \(WA\) ,本地输出了一下 \(1 \sim 10^8\) 所有 \(n\) 的解,发现还是有一些达到了 \(10^{11}\) ,被卡的很难受.
解决方法也很简单,多构造几组呗..在我不断 \(WA\) ,构造, \(WA\) ,构造 的努力下..于是代码变成了如下画风.....
#include<stdio.h>
#include<iostream>
#include<algorithm>
#define pb push_back
using namespace std;
#define int long long
int u[7]={3,7,31,127,8191,131071,524287};
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin>>T;
while(T--)
{
int n;
cin>>n;
if (n % 2 == 0)
{
cout << n << " " << n * 2 << endl;
}
else if (n % 3 != 0)
{
cout << n * 2 << " " << n * 3 << endl;
}
else if (n % 3 == 0 && n % 7 != 0)
{
cout << n * 48 << " " << n * 49 << endl;
}
else if (n % 3 == 0 && n % 11 != 0)
{
cout<<n * 32<<" "<<n*33<<endl;
}
else if(n%3==0&&n%13!=0)
{
cout<<n * 12<<" "<<n*13<<endl;
}
else if(n%3==0&&n%17!=0)
{
cout<<n * 17<<" "<<n*18<<endl;
}
else if(n%3==0 &&n%19!=0)
{
cout<<n * 18<<" "<<n*19<<endl;
}
else if(n%3==0&&n%23!=0)
{
cout<<n*23<<" "<<n*24<<endl;
}
else if(n%3==0&&n%31!=0)
{
cout<<n*31<<" "<<n*32<<endl;
}
else if(n%5==0&&n%7!=0)
{
cout<<n * 49<<" "<<n*50<<endl;
}
else
{
for(int i =0;i<7;i++)
{
if(n%u[i]!=0)
{
cout<<n*u[i]<<" "<<n*(u[i]+1)<<endl;
break;
}
}
}
}
return 0;
}
最后交上去终于是 \(AC\) 了!!喜大普奔!!
然后来看一下官方标程:

J.Two Kings
国际象棋模拟器,两个棋子每步可以向以其自身周围的8个方格中移动一次.一个棋子如果到了另一个棋子周围的 \(8\) 个方格之内,则会被吃掉.两个人分别操纵一个棋子, \(Walk\ Alone\) 先走,如果他能走到 \(x\) 轴的无穷远处,即获胜,如果无论如何他不能走到无穷远处,则他的对手获胜.
首先,由于 \(W\) 先走,如果对手在上面,他可以往右下走,如果对手在上面,则可以往右上走.两个棋子同时向上或向下时,他们的纵坐标之差不变,横坐标之差.所以如果开始时两个棋子纵坐标距离相差大于 \(1\) ,那么无论如何对手都不能阻挡住 \(W\) .如果相差等于 \(1\) ,考虑到 \(W\)先走,一定是当 \(W\) 的对手走完时他们的纵坐标相差 \(1\) .当他们横坐标相差大于 \(1\)时, \(W\) 正常往右上(右下)走就可以了,当其中一个人走完以后横坐标相差为 \(1\) 时,这个人如果是 \(W\) ,那么 \(W\) 就在对手的 \((x-1,y-2)\) 处,容易发现对手阻挡不了 \(W\) ,如果是 对手 ,那么此时 \(W\) 在对手的 \((x-1,y-1)\) 处,对手走到了 \(W\) 的可吃范围内,显然也会输.
因此得到结论
- 当他们横坐标之差大于 \(0\) 时, \(W\) 一定获胜.
下面讨论他们在同一行的情况
如果 任意一方 走完以后他们俩横坐标相差 \(1\) , 显然 走的那一方 输.
所以下面考虑走之前的情况,此时他们俩横坐标相差 \(2\)
如果 \(W\) 走, \(W\) 只能往下, 此时 对手也往下 , \(W\) 不可能获胜.
如果 对手走,对手无论往上还是往下, \(W\) 向右+其相反方向的方向走即可,此时对手就拦不到他了.
注意到: 从开始到他们俩相遇之前, 对手不可以往上下走,只能往他们俩对面的方向走 ,否则就转化到 横坐标之差不相等的情况了,那时候 \(W\) 必赢.
因此每一次回合下来他们的横坐标之差都减 \(2\).所以如果最开始的横坐标之差为奇数,那么就是 \(W\) 走完一格以后横坐标之差变为偶数,每一次减 \(2\), 这个偶数迟早有被减到 \(2\) 的时候 , 所以 \(W\)迟早会赢.如果偶数,同理,对手获胜.
即:开始时,若他们横坐标相同(且 \(W\) 在对手的左边),他们横坐标相差为奇数时, \(W\) 赢,否则 对手赢.

