HDU 5640.King's Cake

King's Cake
Time Limit:1000MS     Memory Limit:65536KB     64bit IO Format:%I64d & %I64u

Description

It is the king's birthday before the military parade . The ministers prepared a rectangle cake of size n \times m(1\le n, m \le 10000) . The king plans to cut the cake himself. But he has a strange habit of cutting cakes. Each time, he will cut the rectangle cake into two pieces, one of which should be a square cake.. Since he loves squares , he will cut the biggest square cake. He will continue to do that until all the pieces are square. Now can you tell him how many pieces he can get when he finishes.

Input

The first line contains a number T(T \leq 1000), the number of the testcases. 

For each testcase, the first line and the only line contains two positive numbers n , m(1\le n, m \le 10000).

Output

For each testcase, print a single number as the answer.

Sample Input

2 2 3 2 5

Sample Output

3 4 hint: For the first testcase you can divide the into one cake of $2\times2$ , 2 cakes of $1\times 1$
 
把长方形按照一刀一刀切成正方形，最后求出所有正方形的个数
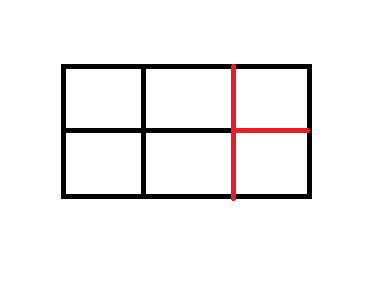
如图，2*3的长方形，第一刀可以分割成2*2的正方形和1*2的长方形；
第二刀可以分成两个1*1的正方形
即3个正方形
 
可以看出，对于一个n*m的长方形（n>m），其操作为分成m*m的正方形和(n-m)*m的长方形
 
提取出相同的操作，写成递归来统计个数
1 //a长 b宽
2 int DFS(int a, int b) {
3     if (a == b)
4         return 1;
5     return 1 + DFS(max(a - b, b), min(a - b, b));
6 
7 }

 

完整代码如下

 

 1 /*
 2 By:OhYee
 3 Github:OhYee
 4 Email:oyohyee@oyohyee.com
 5 Blog:http://www.cnblogs.com/ohyee/
 6 
 7 かしこいかわいい？
 8 エリーチカ！
 9 要写出来Хорошо的代码哦~
10 */
11 #include <cstdio>
12 #include <algorithm>
13 #include <cstring>
14 #include <cmath>
15 #include <string>
16 #include <iostream>
17 #include <vector>
18 #include <list>
19 #include <queue>
20 #include <stack>
21 using namespace std;
22 
23 //DEBUG MODE
24 #define debug 0
25 
26 //循环
27 #define REP(n) for(int o=0;o<n;o++)
28 
29 //a长 b宽
30 int DFS(int a, int b) {
31     if (a == b)
32         return 1;
33     return 1 + DFS(max(a - b, b), min(a - b, b));
34 
35 }
36 
37 void Do() {
38     int n, m;
39     scanf("%d%d", &n, &m);
40     printf("%d\n", DFS(max(m, n), min(m, n)));
41 }
42 
43 
44 int main() {
45     int T;
46     scanf("%d", &T);
47     while (T--)
48         Do();
49     return 0;
50 }

 

posted @ 2016-04-17 00:06  OhYee  阅读(88)  评论(0)  编辑  收藏  举报