2022年北航面向对象程序设计第一单元总结

2022年北航面向对象程序设计第一单元总结

目录

• 2022年北航面向对象程序设计第一单元总结
  • HW1
    • 设计思路
      • UML图
      • 解析
      • 运算和化简
    • 程序分析
    • bug分析
    • 测试思路
    • 综合评价
  • HW2&&HW3
    • 设计思路
      • UML图
      • 解析
      • 运算和化简
    • 程序分析
      • 附：度量分析条目解释
    • bug分析
    • 测试思路
    • 综合评价
  • 补充方法
    • 重写equals和hashcode方法
    • 重写clone方法和序列流
    • 重写toString方法和调试
    • remove使用时的注意事项
  • Hack策略
  • 架构设计体验
    • 整体架构
      • 解析方法
      • sin cos和运算的处理
    • 构造细节
      • 字符串传递、字符串构造
      • 重写equals，toString，hashCode，clone方法
    • 进一步的化简
  • 心得体会

HW1

设计思路

UML图

解析

首先在ExpressionDemo里面初始化字符串，在初始字符串层级保证输入的合法化

然后传入到Expression上，构造根表达式，这时先通过toSuffix解析把每个元素解析成一个组成元素（Element或Operator）存在了Stack里，这时便有了运算顺序与各个需要运算的单元

运算和化简

从Stack里逐个取组成元素先转移成Polynomial然后把Polynomial作为运算单元进行计算，中间的结果通过Set和Map可以很好地达到合并的目的，运算与化简便可同时执行

程序分析

类方法	CogC	ev(G)	iv(G)	v(G)
Element.Element()	0.0	1.0	1.0	1.0
Element.Element(BigInteger)	0.0	1.0	1.0	1.0
Element.Element(BigInteger, char, int)	0.0	1.0	1.0	1.0
Element.Element(char, int)	0.0	1.0	1.0	1.0
Element.equalLeftParentheses()	0.0	1.0	1.0	1.0
Element.expressionToString()	0.0	1.0	1.0	1.0
Element.getBy()	0.0	1.0	1.0	1.0
Element.getCoefficient()	0.0	1.0	1.0	1.0
Element.getIndex()	0.0	1.0	1.0	1.0
Element.setBy(char)	0.0	1.0	1.0	1.0
Element.setCoefficient(BigInteger)	0.0	1.0	1.0	1.0
Element.setIndex(int)	0.0	1.0	1.0	1.0
Expression.calAdd(Polynomial, Polynomial)	8.0	1.0	4.0	4.0
Expression.calculate()	8.0	1.0	4.0	8.0
Expression.calMapMul(Map, Map)	7.0	1.0	4.0	4.0
Expression.calMul(Polynomial, Polynomial)	7.0	1.0	4.0	4.0
Expression.calPow(Polynomial, Polynomial)	6.0	3.0	5.0	5.0
Expression.calSub(Polynomial, Polynomial)	8.0	1.0	4.0	4.0
Expression.Expression()	0.0	1.0	1.0	1.0
Expression.Expression(ArrayList)	0.0	1.0	1.0	1.0
Expression.Expression(Component)	0.0	1.0	1.0	1.0
Expression.Expression(String)	0.0	1.0	1.0	1.0
Expression.getExpression()	0.0	1.0	1.0	1.0
Expression.getSt()	0.0	1.0	1.0	1.0
Expression.getSuffix()	0.0	1.0	1.0	1.0
Expression.priority(Component)	2.0	6.0	1.0	6.0
Expression.setExpression(Stack)	0.0	1.0	1.0	1.0
Expression.setSt(Stack)	0.0	1.0	1.0	1.0
Expression.setSuffix(ArrayList)	0.0	1.0	1.0	1.0
Expression.toSuffix(String)	41.0	1.0	23.0	24.0
ExpressionDemo.headDelete(String)	30.0	1.0	24.0	25.0
ExpressionDemo.init(String)	41.0	1.0	23.0	23.0
ExpressionDemo.main(String[])	0.0	1.0	1.0	1.0
ExpressionDemo.oneJudge(String, int)	2.0	1.0	2.0	2.0
ExpressionDemo.subAccording(String, int, int)	2.0	1.0	2.0	2.0
ExpressionDemo.threeJudge(String, int)	12.0	1.0	8.0	8.0
ExpressionDemo.twoJudge(String, int)	6.0	1.0	4.0	4.0
Operator.equalLeftParentheses()	0.0	1.0	1.0	1.0
Operator.expressionToString()	2.0	1.0	2.0	2.0
Operator.getFh()	0.0	1.0	1.0	1.0
Operator.Operator()	0.0	1.0	1.0	1.0
Operator.Operator(char)	0.0	1.0	1.0	1.0
Operator.setFh(char)	0.0	1.0	1.0	1.0
Polynomial.getPolynomial()	0.0	1.0	1.0	1.0
Polynomial.Polynomial()	0.0	1.0	1.0	1.0
Polynomial.Polynomial(Integer, BigInteger)	0.0	1.0	1.0	1.0
Polynomial.Polynomial(Map)	0.0	1.0	1.0	1.0
Polynomial.polynomialToString()	30.0	6.0	10.0	12.0
Polynomial.printIndex1(BigInteger)	3.0	1.0	3.0	3.0
Polynomial.printIndex2(BigInteger)	3.0	1.0	3.0	3.0
Polynomial.printIndexNormal(Integer, BigInteger)	3.0	1.0	3.0	3.0
Polynomial.printPos()	9.0	3.0	6.0	6.0
Polynomial.setPolynomial(Map)	0.0	1.0	1.0	1.0
Total	230.0	67.0	172.0	185.0
Average	4.34	1.26	3.25	3.49

bug分析

第一次的作业的代码经过了10w次的随机数据测试，但最后还是出现了一个bug

x**+00

对于这种x的指数是0并且有前导0的情况，我的字符串处理函数会把他们都删除掉，指数部分就出现了问题，后面接任何逻辑都会出现无法解析的错误

测试思路

测试过程中分了一些特殊的数据与随机数据进行检测，由于评测机的效果非常好，所以从周三写完的时候就一直在评测了，各种数据跑了超过了10w组，并做了相关的取正项放第一位和x**2转换x*x的优化

综合评价

第一次作业总体上比较简单，一上午就写完了，个人感觉第一次作业栈解析的优势还是很明显的，各个单元在初始化的优先级是相同的，而不是递归地去解析，这样的意义在于处理过程的耦合度更低，相比于递归解析+化简，这种方法调试起来非常方便，各个模块的功能分化也非常地明显，最后的bug也很好调，只需要额外加入一行正则表达式替换

HW2&&HW3

我自己的HW2与HW3用的完全是一个代码，因为一直允许递归嵌套解析和计算，所以到了HW3只是de了一下HW2强测的bug

设计思路

UML图

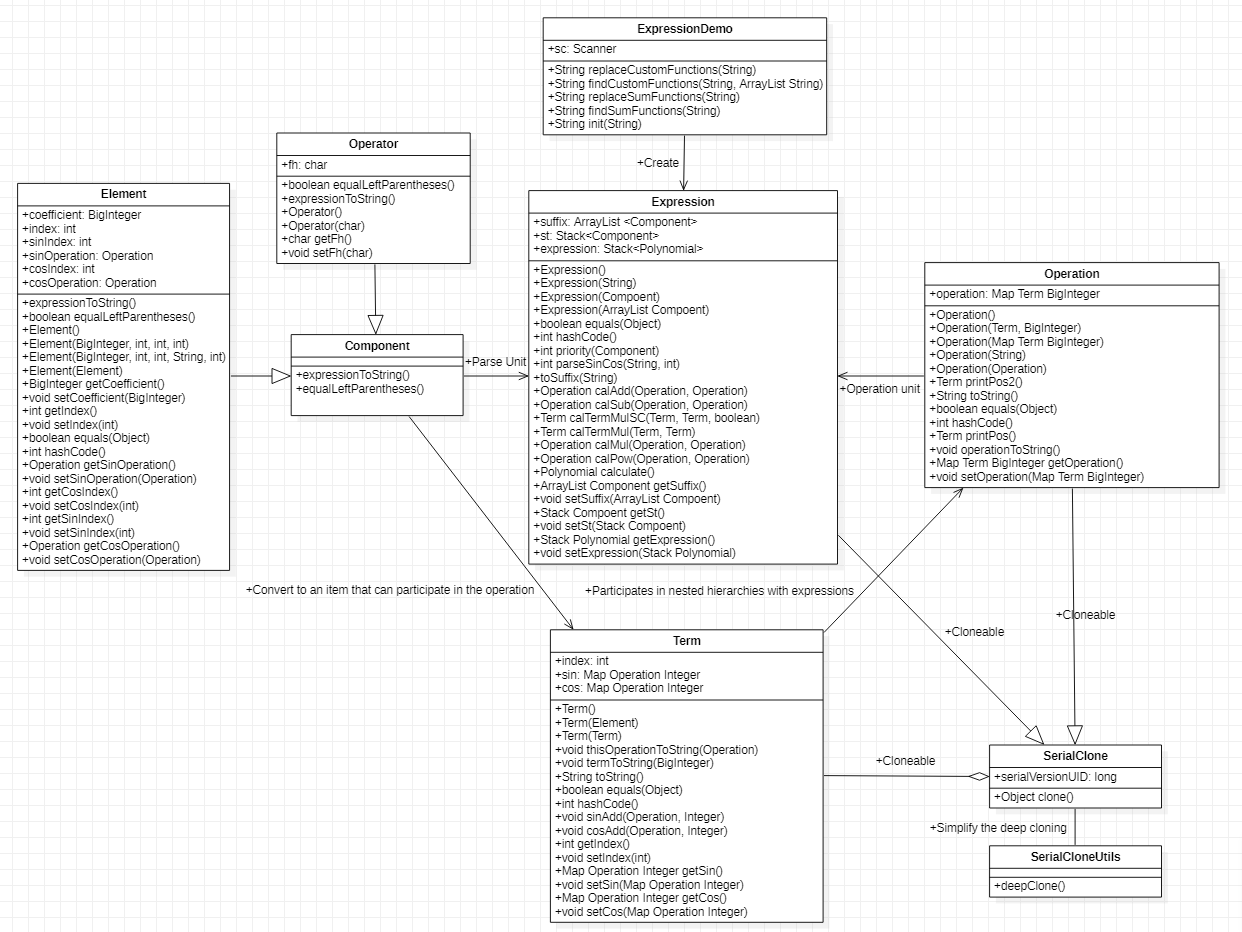
解析

仍旧是在ExpressionDemo里面初始化字符串，在初始字符串层级保证输入的合法化，不同的是这次采用更为便捷理解和维护的replaceAll来完成字符串的处理，虽然看上去有些冗杂，但是非常直观有效

public static String init(String str, ArrayList<String> func) {
    String s = str.replaceAll(" ", "");
    s = s.replaceAll("\t", "");
    s = findSumFunctions(s);
    s = findCustomFunctions(s, func);
    s = s.replaceAll(" ", "");
    s = s.replaceAll("\t", "");
    if (s.charAt(0) == '+' || s.charAt(0) == '-') {
        s = '0' + s;
    }
    s = s.replaceAll("(?<=[^0-9])(0+(?=[0-9]))","");
    s = s.replaceAll("^(0+)","");
    s = s.replaceAll("\\+{3}","+");
    s = s.replaceAll("\\-{3}","-");
    s = s.replaceAll("\\+\\-\\-","+");
    s = s.replaceAll("\\-\\+\\+","-");
    s = s.replaceAll("\\+\\+\\-","-");
    s = s.replaceAll("\\-\\-\\+","+");
    s = s.replaceAll("\\+\\-\\+","-");
    s = s.replaceAll("\\-\\+\\-","+ ");
    s = s.replaceAll("\\+\\-","-");
    s = s.replaceAll("\\-\\+","-");
    s = s.replaceAll("\\+{2}","+");
    s = s.replaceAll("\\-{2}","+");
    //sin cos
    s = s.replaceAll("\\+x","+1*x");
    s = s.replaceAll("\\+sin","+1*sin");
    s = s.replaceAll("\\+cos","+1*cos");
    s = s.replaceAll("\\+\\(","+1*(");
    s = s.replaceAll("\\-x","-1*x");
    s = s.replaceAll("\\-sin","-1*sin");
    s = s.replaceAll("\\-cos","-1*cos");
    s = s.replaceAll("\\-\\(","-1*(");
    s = s.replaceAll("\\(\\+","(0+");
    s = s.replaceAll("\\(\\-","(0-");
    s = s.replaceAll("\\*\\*\\+","**");
    s = s.replaceAll("\\*\\+","*");
    s = s.replaceAll("\\*\\-","*(0-1)*");
    s = s.replaceAll("^\\+","");
    s = s.replaceAll(" ", "");
    s = s.replaceAll("\t", "");
    //System.out.println(s);
    return s;
}

对于本次的自定义函数和求和函数，我仍旧使用栈思想来进行解析和替换。实际是使用一个变量记录当前的左括号加入数量，如果加入右括号就使变量自减，左括号就自加，这时这个变量为1时对应的位置即为可以替换的字符串，然后通过正则表达式的Pattern和Matcher便很好的完成了字符串的替换。

在第三次作业中加入了嵌套时这种方法的优势很明显。（PS：第二次作业的时候我本来的打算是等第三次作业再加入求和函数和自定义函数互相嵌套这种情况，但第三次作业没出这个，反倒是求和函数不允许套自定义函数和求和函数，只有自定义函数可以嵌套，我目前的解析方式求和函数和自定义函数都是可以嵌套自身的，看起来还多了个功能😄）

然后同样是替换后传入到Expression上，构造根表达式，然后通过toSuffix解析把每个元素解析成一个组成元素（Element或Operator）存在了Stack里

运算和化简

这个与第一次相同的是从Stack里逐个取组成元素，但本次新添的部分为先将Element类转换为Term类，因为sin和cos仅有单一的状态易于解析，而运算时则需要一个sin情况下的表达式列表，所以一定是需要这个转换的，接下来就很简单了，还是同第一次一样，只是把Polynomial换个名为Operation，先转移成Term，然后把Term加入Operation作为Operation的初始元素，然后把Operation作为运算单元进行计算，中间的结果通过Set和Map同样可以很好地达到合并的目的（此处唯一与前面的不同是要写equals方法，不然有时会出现明明表达式相同却合并不了的情况，出现这种情况的原因是这些表达式生成的方式不一样（比如有的是计算来的，有的是构造时候就直接生成的，或者计算时生成的方式不一样等等），内存映射的并不是同一处的表达式），运算与化简也可同时执行

程序分析

类方法	CogC	ev(G)	iv(G)	v(G)
Element.Element()	0.0	1.0	1.0	1.0
Element.Element(BigInteger, int, int, int)	0.0	1.0	1.0	1.0
Element.Element(BigInteger, int, int, String, int)	2.0	1.0	1.0	2.0
Element.Element(Element)	0.0	1.0	1.0	1.0
Element.equalLeftParentheses()	0.0	1.0	1.0	1.0
Element.equals(Object)	7.0	4.0	2.0	4.0
Element.expressionToString()	0.0	1.0	1.0	1.0
Element.getCoefficient()	0.0	1.0	1.0	1.0
Element.getCosIndex()	0.0	1.0	1.0	1.0
Element.getCosOperation()	0.0	1.0	1.0	1.0
Element.getIndex()	0.0	1.0	1.0	1.0
Element.getSinIndex()	0.0	1.0	1.0	1.0
Element.getSinOperation()	0.0	1.0	1.0	1.0
Element.hashCode()	0.0	1.0	1.0	1.0
Element.setCoefficient(BigInteger)	0.0	1.0	1.0	1.0
Element.setCosIndex(int)	0.0	1.0	1.0	1.0
Element.setCosOperation(Operation)	0.0	1.0	1.0	1.0
Element.setIndex(int)	0.0	1.0	1.0	1.0
Element.setSinIndex(int)	0.0	1.0	1.0	1.0
Element.setSinOperation(Operation)	0.0	1.0	1.0	1.0
Expression.calAdd(Operation, Operation)	8.0	1.0	4.0	4.0
Expression.calculate()	8.0	1.0	4.0	8.0
Expression.calMul(Operation, Operation)	9.0	1.0	6.0	6.0
Expression.calPow(Operation, Operation)	38.0	10.0	14.0	14.0
Expression.calSub(Operation, Operation)	8.0	1.0	4.0	4.0
Expression.calTermMul(Term, Term)	2.0	1.0	3.0	3.0
Expression.calTermMulSC(Term, Term, boolean)	25.0	4.0	11.0	11.0
Expression.equals(Object)	3.0	4.0	2.0	4.0
Expression.Expression()	0.0	1.0	1.0	1.0
Expression.Expression(ArrayList)	0.0	1.0	1.0	1.0
Expression.Expression(Component)	0.0	1.0	1.0	1.0
Expression.Expression(String)	0.0	1.0	1.0	1.0
Expression.getExpression()	0.0	1.0	1.0	1.0
Expression.getSt()	0.0	1.0	1.0	1.0
Expression.getSuffix()	0.0	1.0	1.0	1.0
Expression.hashCode()	0.0	1.0	1.0	1.0
Expression.parseSinCos(String, int)	18.0	3.0	10.0	12.0
Expression.priority(Component)	2.0	6.0	1.0	6.0
Expression.setExpression(Stack)	0.0	1.0	1.0	1.0
Expression.setSt(Stack)	0.0	1.0	1.0	1.0
Expression.setSuffix(ArrayList)	0.0	1.0	1.0	1.0
Expression.toSuffix(String)	42.0	1.0	26.0	26.0
ExpressionDemo.findCustomFunctions(String, ArrayList)	16.0	5.0	5.0	7.0
ExpressionDemo.findSumFunctions(String)	10.0	4.0	4.0	6.0
ExpressionDemo.init(String, ArrayList)	2.0	1.0	2.0	3.0
ExpressionDemo.main(String[])	1.0	1.0	2.0	2.0
ExpressionDemo.replaceCustomFunctions(String, String)	4.0	1.0	5.0	5.0
ExpressionDemo.replaceSumFunctions(String)	10.0	2.0	5.0	11.0
Operation.equals(Object)	3.0	3.0	2.0	4.0
Operation.getOperation()	0.0	1.0	1.0	1.0
Operation.hashCode()	0.0	1.0	1.0	1.0
Operation.Operation()	0.0	1.0	1.0	1.0
Operation.Operation(Map)	1.0	1.0	2.0	2.0
Operation.Operation(Operation)	1.0	1.0	2.0	2.0
Operation.Operation(String)	0.0	1.0	1.0	1.0
Operation.Operation(Term, BigInteger)	0.0	1.0	1.0	1.0
Operation.operationToString()	24.0	6.0	7.0	9.0
Operation.printPos()	3.0	3.0	3.0	3.0
Operation.printPos2()	3.0	3.0	3.0	3.0
Operation.setOperation(Map)	0.0	1.0	1.0	1.0
Operation.toString()	28.0	6.0	7.0	11.0
Operator.equalLeftParentheses()	0.0	1.0	1.0	1.0
Operator.expressionToString()	2.0	1.0	2.0	2.0
Operator.getFh()	0.0	1.0	1.0	1.0
Operator.Operator()	0.0	1.0	1.0	1.0
Operator.Operator(char)	0.0	1.0	1.0	1.0
Operator.setFh(char)	0.0	1.0	1.0	1.0
SerialClone.clone()	0.0	1.0	1.0	1.0
SerialCloneUtils.deepClone(T)	1.0	1.0	2.0	2.0
Term.cosAdd(Operation, Integer)	0.0	1.0	1.0	1.0
Term.equals(Object)	4.0	3.0	2.0	6.0
Term.getCos()	0.0	1.0	1.0	1.0
Term.getIndex()	0.0	1.0	1.0	1.0
Term.getSin()	0.0	1.0	1.0	1.0
Term.hashCode()	0.0	1.0	1.0	1.0
Term.setCos(Map)	0.0	1.0	1.0	1.0
Term.setIndex(int)	0.0	1.0	1.0	1.0
Term.setSin(Map)	0.0	1.0	1.0	1.0
Term.sinAdd(Operation, Integer)	0.0	1.0	1.0	1.0
Term.Term()	0.0	1.0	1.0	1.0
Term.Term(Element)	0.0	1.0	1.0	1.0
Term.Term(Term)	2.0	1.0	3.0	3.0
Term.termToString(BigInteger)	21.0	1.0	14.0	14.0
Term.thisOperationToString(Operation)	4.0	1.0	4.0	4.0
Term.toString()	18.0	1.0	7.0	12.0
Total	330.0	136.0	223.0	267.0
Average	3.88	1.60	2.62	3.14

附：度量分析条目解释

• OC：类的非抽象方法圈复杂度，继承类不计入
• WMC：类的总圈复杂度
• ev(G)：非抽象方法的基本复杂度，用以衡量一个方法的控制流结构缺陷，范围是 [1, v(G)]
• iv(G)：方法的设计复杂度，用以衡量方法控制流与其他方法之间的耦合程度，范围是 [1, v(G)]
• v(G)：非抽象方法的圈复杂度，用以衡量每个方法中不同执行路径的数量

bug分析

本次强测和互测查出了两个bug，一个是同名函数多参数嵌套会解析错误

1
f(x,y)=(((sin(cos(x))-(+1-sin(cos(y))))))
(f(f(x,x**1),x**+1)*cos(x)**+01)-(cos(sin((x**2))))-(+098782738)**+03

1
f(x,y)=y-(cos(x)**+3-sin(x)**03)
(f(x**3,f(0,1))-+3*x*sin(x))**2+cos(x)*sum(i,1,5,1)*(+1--cos(x))

还有求和函数在负偶次方下会因符号产生求和错误

0
sum(i,-2,-1,i**+2)

0
sum(i,-01,0,(-i**0))

两个都是情况没考虑全，自己的使用的数据生成器生成的数据量过大，出现这种异常的时候被自己误以为成了不合法数据，还是自己的测试不到位吧，直到周六晚交上才开始写评测机，其实评测机写的也很快，确实是应当先去写评测机然后再返回测试的

测试思路

在这里不得不感谢ysyxgg的数据生成器，我只在他的数据生成器上做了比较小的改动，然后加了几个参数用来调节数据的生成方向便达到了非常好的测试效果，生成细节在这里大概讲讲我的理解，有需要进一步了解的同学可以去看ygg的blogOO_Lab0_表达式的展开 - 青衫染墨 - 博客园 (cnblogs.com)，然后具体测试细节我放在了下面的Hack策略中

首先肯定是按照题目中的形式化表述来生成测试数据更为方便，并且对应的因子的函数以及题目中的数据限制要求也更好满足，所以可以看到ygg单独定义的每个因子的生成函数以及函数嵌套

class DiyFunct:
	···
def getDiyFunct():
	···
def generate_#(depth = 0,nest = 0,control = 0):
	···
def generate_T(depth = 0,nest = 0,control = 0):
	···
def generate_Sum():
	···

这里就不展示太多细节了，总的来说就是模拟出形式化表述，然后生成对应的因子，然后组成一个表达式，把生成表达式也封装成一个函数便可以对sin、cos等递归嵌套，便有了有效的数据，然后可以根据测试要求在已有数据生成器的基础上限制指数、括号层级，以及可以在最终生成的数据中加入Cost的过滤

综合评价

第二三次作业说心里话确实感觉不是很难，但自己这两周因为各种事情把进度给拖下来了，导致第二周的强测寄寄，重构后非合并提交扣了不少分，第三周的话优化做得也一般，性能分不是非常高，感觉功夫用错地方了，但好在长了个见识，以后一定要提前做OO

补充方法

或许这里开始才是重点（x

不管怎么说，这里开始才是我后两次作业对自己成绩不太满意的根本原因。其实几次作业从程序和编程思维的角度上讲并没有什么太大差别，思维量并不是非常大，实现起来也很容易，但bug却很容易出现在Java内部的一些机制上，我这里针对我碰到的这几个令我自己有些许崩溃的点来补充一下

重写equals和hashcode方法

重写equals方法是化简合并同类项的关键一步，只有完全确保各种情况的合并才不会因为递归而把合并的问题放大，equals可以和排序一同使用，但我这里输出和比较等等都是没有使用排序的（换种说法就是没有使用自定义方法判断不太需要排序），而重点需要的部分是equals来确保各个对象的相等判断

其中Java内置的equals的方法如下

public boolean equals(Object obj) {
	return (this == obj);
}

实际上就是直接判断对象的地址，只有完全引用同一对象的时候才认为相同，这在我们合并同类项计算的时候对我们来说是非常不利的，甚至这种情况连常数项的化简效果都难以完全满足，所以自定义equals是不可避免的

下面先来介绍一下错误写法

@override
private boolean equals(HashSet<Element> aa, HashSet<Element> bb) {
    HashSet<Element> a = new HashSet<>(aa);
    HashSet<Element> b = new HashSet<>(bb);
    Iterator<Element> it1 = a.iterator();
    Iterator<Element> it2 = b.iterator();
    while (it1.hasNext()) {
        Element ea = it1.next();
        while (it2.hasNext()) {
            Element eb = it2.next();
            boolean judge = ea.getIndex() == eb.getIndex();
            boolean judge1 = ea instanceof X && eb instanceof X;
            boolean judge2 = ea instanceof Sin && eb instanceof Sin && ((Sin) ea).getUnfoldOperation() == ((Sin) eb).getUnfoldOperation();
            boolean judge3 = ea instanceof Cos && eb instanceof Cos && ((Cos) ea).getUnfoldOperation() == ((Cos) eb).getUnfoldOperation();
            if (judge && (judge1 || judge2 || judge3)) {
                it1.remove();
                it2.remove();
            }
        }
    }
    return a.size() == 0 && b.size() == 0;
}

这种写法是我刚开始做第二次作业的时候的写法，后来因为de不出bug被迫重构，但错误在重构后再次出现，最后问题确定为迭代器的remove问题，它会导致原来的对象被删除，经过与wl的强烈battle后，才发现自己这个沙雕问题（x，所以一定不要自定义Set，Map等数据结构工具的比较！一定不要自定义Set，Map等数据结构工具的比较！一定不要自定义Set，Map等数据结构工具的比较！

然后是正确的equals写法

@Override
public boolean equals(Object obj) {
    if (this == obj) {
        return true;
    }
    if (obj == null || this.getClass() != obj.getClass()) {
        return false;
    }
    Operation op = (Operation) obj;
    return Objects.equals(operation, op.getOperation());
}

这里的operation一个Map，直接调用Java Objects提供的equals就可以完成这个的比较，而且实测效果很完美

重写clone方法和序列流

深浅克隆是又一个避免remove问题的解决方法，我在实际debug的过程中，就是深克隆先解决了一定的bug然后再通过equals方法的转变解决的另一处的remove导致的bug

深克隆可以非常好地解决非方法封装下的remove的问题，使用深克隆可以将一个对象的生命周期等价到更高阶对象的生命周期，更有利于我们维护对象的生命周期

经过wl的点拨，我学习了wl讲的重写clone方法，比较无奈的是，我当会了重写clone时，在我的程序中加入clone方法的重写会巨额增大我的代码量，并且由于使用clone的方法处众多，需要修改的地方也很多，于是最终选择了序列化的方式通过序列流的正反解来达到深克隆，这种写法比较方便，但是对于final类型的成员变量不是很友好，它的定义就被模糊化了，所以这里把两种方法都列出，供使用者参考吧

先是重写clone方法

public class Term extends SerialClone {
    private int index;
    private Map<Operation, Integer> sin = new HashMap<>();
    private Map<Operation, Integer> cos = new HashMap<>();
    ··· ···
    @Override
    protected Term clone() {
        //return (Operation)super.clone();
        Term p=null;
        try{
            p=(Term)super.clone();
            p.sin=sin.clone();
            p.cos=cos.clone();
        }catch(CloneNotSupportedException e){
            throw new RuntimeException(e);
            //e.printStackTrace();
        }
        return p;
    }
}

可以总结到的规律是类内的对象均需要再调一次.clone方法，并且类内的对象也一定要支持.clone方法，也即被克隆的部分要支持深克隆

接下来介绍一下序列化与反序列化的完成深克隆的方法

import java.io.ByteArrayInputStream;
import java.io.ByteArrayOutputStream;
import java.io.IOException;
import java.io.InputStream;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.io.Serializable;

public class SerialCloneUtils {
    /**
     * 类名SerialCloneUtils
     * 使用ObjectStream序列化实现深克隆
     * @return Object obj
     */
    public static <T extends Serializable> T deepClone(T t) throws CloneNotSupportedException {
        // 保存对象为字节数组
        try {
            ByteArrayOutputStream bout = new ByteArrayOutputStream();
            try (ObjectOutputStream out = new ObjectOutputStream(bout)) {
                out.writeObject(t);
            }

            // 从字节数组中读取克隆对象
            try (InputStream bin = new ByteArrayInputStream(bout.toByteArray())) {
                ObjectInputStream in = new ObjectInputStream(bin);
                return (T) (in.readObject());
            }
        } catch (IOException | ClassNotFoundException e) {
            CloneNotSupportedException cloneNotSupportedException;
            cloneNotSupportedException = new CloneNotSupportedException();
            e.initCause(cloneNotSupportedException);
            throw cloneNotSupportedException;
        }
    }
}

import java.io.Serializable;
/**
 * 类名 SerialClone
 * 描述 序列化克隆类，只要继承该类，就可以实现深克隆
 *
 */
public class SerialClone implements Cloneable, Serializable {
    private static final long serialVersionUID = 5794148504376232369L;

    @Override
    public Object clone() throws CloneNotSupportedException {
        return SerialCloneUtils.deepClone(this);
    }
}

后面则仅需要继承SerialClone类便可完成深克隆，当已有继承关系时可以在顶层继承该类，同样可以完成深克隆的目的，唯一需要加入的就是需要调用深克隆时在对应的方法处加入throws CloneNotSupportedException，这里IDEA会有提示，直接安装提示加入即可

重写toString方法和调试

这里重写toString的方法的目的就是为了调试，实际上重写toString方法还有一个好处，因为我们常常习惯性的直接写输出函数（或者说是我常常酱紫(●ˇ∀ˇ●)），但这种方式对应的亏也在第一次作业迭代到后面的时候出现了，第一次作业的时候输出逻辑很简单，但第二三次的输出逻辑就变得很复杂了，特别还是越优化越复杂，如果直接用每一个类中的参数去输出，很难提高多个类耦合输出下的输出优化度，而重写toString可以帮我们留下一个后路，就是把输出先转换为字符串，而字符串输出保存后可以多次利用，而一个字符串的优化潜能我也不必多说了，毕竟输入就是字符串嘛doge，而toString还有一个便利，就是在调试的时候可以直接通过toString查看当前调试的信息，不需要我们人工地总是通过变量的值来观察项到底是什么，会把调试的效率提高很多，特别是在迭代到后面的调试难度非常大的时候，重写toString方法非常有意义，效果如下图

remove使用时的注意事项

至此，我想说的就是，remove真的是万恶之源，建议需要使用remove的地方在类内专门设置一个remove对应的标记来判断，然后remove前到涉及remove的操作结束后都对标记进行维护，虽然效率低了点但也不至于太低，相比于java的深拷贝机制，似乎这种傻乎乎的标记还能快出来一点（x

我这两周的bug全部集中在了remove上的表现，remove真的是万恶之源，同时remove迭代器也会影响原对象，所以除非遇到情况非常合适，后面不打算使用相应对象的时候，否则千万不要remove

对于remove避免不了的问题，比如我已经按照remove的方式写完了对应的部分，那就只能通过深克隆的方式解决显式对象的问题，然后再通过方法重写，方法内部克隆来解决被封装起来的方法的问题

最后再来一句忠告，没事千万别用remove

Hack策略

第一次互测的时候，感觉数据限制实在太大了，第一次互测只Hack到了三次，但实际我在自己本地测出来了非常非常多的bug，但无法提交评测机。第二次由于remove的问题，我没有参与互测。第三次互测的时候，我用了ysyxgg的数据生成器，通过自己评测机的性能成功Hack了18次，也帮几位hxdHack了几次(*^▽^*)，后面介绍介绍Hack方式吧

首先就是数据包的形式，我的建议，就是直接打包jar，.class文件的运行效率真的比不了.jar，通过随机数据的方式进行评测，运行效率和运行稳定性是获取高额Hack数据的关键，而高额Hack数据又是避免同质bug的关键

其实通过bug修复的规则可以发现，bug修复的设置其实多少会有些问题，在java中很多小bug根本不需要5行来修复，在良好的考虑了会出bug的位置，加入了正则表达式接口后，甚至很难是有bug是需要用两行去修的（至少我现在碰到的bug全部一行解决），这样5行能修5个bug，而且是免审批的，这对于Hack人来说，很容易出现多个bug的Hack结果没拿到多个bug的分，反倒因为被判同质而被反扣分，所以一定要确保找到高额同质bug的数据，然后分析每个人的错误点才可以获取更高的bug分数，达到雨露均沾的目的

（打点不必要的码，避免被攻击doge）

因为Hack的规则只有3次以上算是同质bug才会降低相应的bug得分，这里唯一被Hack超过3次的Assassin实际我用了3组不同质的bug Hack到了他，总体上我觉得这算是一个比较好的Hack

针对上述内容，我也写了相应的评测机程序

首先便是打包jar包，这对这种长线的Hack战争有着非常大的意义，使用如下的目录安置各文件（这样越规范的文件目录越利于我们后续的评测机拓展性）

# artifacts <dir>
#     |-- xxxx_jar <dir>
#     |      |-- xxxx.jar
#     |      |-- *Result.txt
#     |-- *submit <dir>
#     |      |-- *stdin1.txt
#     |      |-- *stdout1.txt
#     |-- TestCases <dir>
#     |-- *Result.txt
#     |-- Hacker.py <this>

对于需要人工设置的输入参数我把它设置到一起，names当然是Hack列表，每周的Hack生成一次即可，myName是用于对拍测评的，如果可以通过sympy直接评测那也可以把自己加入到评测目录中，readTestSetFromFile是确认数据来源的，一般来讲随机数据还是主力，找到一个目标后将数据转移到数据文件中，然后改readTestSetFromFile参数为True然后简化数据内容进行精确搜寻，只有搜寻到了更小的范围才能最高程度地避免同治bug。另外两个参数是提醒自己需要人工定义读取数据文件的方式和生产结果文件的方式

names = ["Alterego", "Archer", "Assassin", "Berserker", "Caster", "Lancer", "Rider"]
myName = "oyhd"
readTestSetFromFile = True
testSet = []
ansSet = []

对于测试结果的比较当然就使用sympy的simplify函数了，这里需要额外说明的是，实测的时候有些化简过差的同学会导致simplify的时间过长，这时就可以直接认定他为错误，避免占用评测机资源，不然自己也无法多线程同时进行随机评测和已有Hack数据的范围缩小

def checkAns(standardAns, usrAns):
    if usrAns == None or usrAns == "":
        return False
    cmp = None
    try:
        cmp = simplify(simplify(standardAns) - simplify(usrAns))
    except:
        return False
    finally:
        return cmp == 0

接下来便是将错误信息写入到结果文件，这样有利于去找专门的人的bug以及进行同质比较，丢弃一些已经Hack过的bug数据

def writeUsrRes(student, usrWrongList, usrWrongAns):
    file = open(student + "_jar\\Result.txt", "w")
    length = len(usrWrongList)
    if length == 0:
        file.write("All correct!")
    else:
        file.write(str(length) + " wrong case(s):\n\n")
        for i in range(length):
            file.write(str(i + 1) + "  Case #" + str(usrWrongList[i]) + ":\n")
            file.write("stdin:\n")
            file.write(str(testSet[usrWrongList[i]]) + "\n")
            file.write("stdout:\n")
            file.write(str(usrWrongAns[i]) + "\n")
            file.write("ans:\n")
            file.write(str(ansSet[usrWrongList[i]]) + "\n\n")
    file.close()


def writeTotalRes(totalWrongList, totalWrongSet):
    file = open("Result.txt", "w")
    nOfP = len(names)
    for i in range(nOfP):
        file.write(names[i])
        if len(totalWrongList[i]) == 0:
            file.write(": All correct!\n\n")
        else:
            file.write(": " + str(len(totalWrongList[i])) + " wrong case(s) in total.\n")
            for k in totalWrongList[i]:
                file.write(str(k) + "\t")
            file.write("\n\n")
    file.close()
    nOfWA = len(totalWrongSet)
    tmp = list(totalWrongSet)
    if not os.path.exists("submit"):
        os.makedirs("submit")
    else:
        os.system("del /q submit\\*")
    for i in range(nOfWA):
        file = open("submit\\" + str(i + 1) +"_stdin.txt", "w")
        file.write(str(testSet[tmp[i]]))
        file.close()
        file = open("submit\\" + str(i + 1) +"_stdout.txt", "w")
        file.write(str(ansSet[tmp[i]]))
        file.close()

其余则是正常的遍历每个参与者+subprocess为进程填充数据，奉上一个运行过程截图

至于Hack策略，我认为一个很重要的点是Hack成功率，其实总的看，Hack的CD还是挺长的，而且一个bug多次交还会有同质的风险，对此我的建议是找出每个人的bug后，将bug糅合来交，可以尽量避免“误伤”，同时Hack成功率也能高一些，岂不美哉。同时可以寻找bug出现较多的数据点先行提交，而后对比这些数据点的异同再进一步确认提交方案

在此奉上自己一波7刀的数据和截图（这次总共提交了5次，35中18，51%成功率）

0
sum(i,1,0,i)-sum(i,-3,-1,(i**2-((-(i**2)**2)**0)))

架构设计体验

整体架构

解析方法

我在构造的过程中尝试了递归下降解析和栈解析，递归下降的解析方式的好处是一次性解析到Term部分，不需要解析单元的类型转换（或者说是可以解析完后立刻出现层次结构），更符合表达式的层次化特点；栈解析方式的好处是各解析后各单元的状态更明显，更有利于分析各个单元的状态，同时与运算部分的耦合度更低，更利于分块处理还有便于调试，对于后续化简部分的逻辑也更方便。开始选用的是递归下降解析，但经过多次debug的痛，最终还是选择了栈解析

sin cos和运算的处理

sin cos还有各个运算单独设计一个类写相应的类方法还是直接用一个类融合，这个我选择的还是后者，第二三次作业我开始的时候是sin cos单独设计类，运算的方法都写在了表达式类中，但后来因为过于繁琐的类型下降判断和Map的KeySet的形式需要Map嵌套以及又因需要KeySet的equals方法而被劝退，特别是第二周那会儿，当时重写equals还不是很熟练，也不会深克隆，于是在这种写法下遇到了不小的困难，每次debug的时候都会追踪到Java的Object类的内定义真的很痛苦，以及感觉以及把助教gg问烦了（x，还是感觉把sin cos 多项式写在同一级更透明，对于项的运算也都是在同一个类内进行操作，而不像刚过提到的Map嵌套对项的乘法运算需要遍历Map，maybe这就意味着要remove 😦

构造细节

字符串传递、字符串构造

在解析过程中直接通过字符串的方式来输入一个待解析的表达式可以更好地进行递归，使用一个预解析的则会增大模块的耦合度，化简时也会碰到两个位置都设计同一优化细节，个人感觉两部分的代码协同完成同一个优化保证原有的正确性不变还挺麻烦的，功能分化更明显也更有利于后续拓展

重写equals，toString，hashCode，clone方法

第一周写作业的时候并不需要用到这四个方法，所以写得非常顺，基本写满一个上午的时候就差不多了，但第二次第三次作业因为这些着实非常头疼，以及感觉自己因为开发经验还不足，一直不敢使用Map的equals一直自己写，后来还就是这个问题。。。总之感觉这些问题就很离谱，需要自己多做一些测试，尽量把这种涉及到equals的比较化简还有clone的复制等等都放置到类内进行，确保了这些的稳定，预运算和预化简才能更方便

进一步的化简

我觉得涉及到三角的化简仅靠见招拆招的方式想到一个补一个的方式去化简的效率实在不够高，我觉得真正的化简应该是构造一个化简参数列表，当做类似于正则表达式的匹配的匹配格式，然后每次运算化简后的与这些格式去比较，这样后续需要化简时就会很方便，直接与这些规则比较，并且这种架构还有利于加入试错型化简的方式，毕竟加入了积化和差和和差化积的时候最终的结果是化简还是变复杂也都不一定。此外，在这种框架下加入一些表达式的标准化处理还是有点必要的，比如重写项的compareTo方法，来对项进行一个确定规则的排序，还有保证常数项（或者说其他的第一项的系数恒正，这样可以做sin内表达式为相反数的化简）

我自己想到和听同学说过的化简规则如下(部分只列了其中一部分)

贪心优化
sin(0), cos(0)等常数优化
sin(operation)**(2+p)*cos(operation)**q+sin(operation)**p*cos(operation)**(q+2) （除此以外的其他项的参数相等）
cos(-exp)=cos(exp) (我做了首项为正的规则，这个我本次当做了默认优化)
sin(exp)+sin(-exp)=0
cos(exp)+cos(-exp)=2*cos(exp)
1-sin(exp)**2=cos(exp**2)

试错优化
展开、合并公式(正向多半是可以化简的)
sin(exp1)cos(exp2)+cos(exp1)sin(exp2)=sin(exp1+exp2)
cos(exp1)cos(exp2)-sin(exp1)sin(exp2)=cos(exp1+exp2)
和差化积 积化和差 (因为涉及到系数问题以及修改后可能可以重新进行运算化简，所以当系数不相等时优化效果难说)
sin(exp1+exp2)+sin(exp1-exp2)=2*sin(exp1)*cos(exp2)
2*cos(exp1)*cos(exp2)=cos(exp1+exp2)+cos(exp1-exp2)
倍角公式（这个多半是能化简，但也会涉及到上面的问题,并且当exp里项比较多的时候也未必会优化）
2*sin(exp)*cos(exp)=sin(2*exp)
cos(exp)**2-sin(exp)**2=cos(2*exp)
4*cos(exp)**3-3*cos(exp)=cos(3*exp)
-4*sin(exp)**3+3*sin(exp)=sin(3*exp)

（所以我认为把字符串留下然后一次一次地运算、试错化简还是很有必要的，毕竟运算速度上在本次作业根本不算什么困难，第一次只需要在乘法的时候把x的乘法项指数相加、常数的加减做了程序的运行就已经非常快了，实测一般只需要0.4秒左右，而评测机支持10秒，并且后续的多次试错化简的速度一定会比第一次快很多，所以我觉得我这种试错化简很有意义）

心得体会

最大的体会就是作业要提前写（x，拖到后面就容易没有做优化的时间了，而且第二周的教训告诉我，鬼知道Java这语言到底在不熟的时候会遇到多少bug（x

不过总的来说第一单元的难度还是不大的，怎么都感觉不如往届的求导难，而且表达式的展开总的来看目的还是很明确的（感觉总没求导绕），所以总体上第一单元过的还是要比想象中的舒服一些的，只是自己有点作死，第二周的迷之bug属实整破防了

对于工程的认知，我最大的感受就是工程项目的可拓展性，其实看课程中总提递归下降解析的问题，所以一直对自己的架构有那么一点怀疑，甚至在第三次的时候在纠结去重构还是去优化，但经过详细的讨论以及亲身尝试同学的程序（and Hack房间其他同学的程序调试）才感受到自己的解析方式的优点，我的栈解析自从第一周调好了后后面拓展起来也非常方便，并且真的是没有出过任何的bug，非常非常稳定，相比于同学使用递归下降的解析，每一个单元的不独立性就使调试过程的问题同时又包括了解析问题，而我自己debug的时候基本只在关注计算过程（或者说唯一卡的地方就是项与项相乘得到新的合并项的部分）就真的意识到了架构的各自优势。对于工程的拓展性，自己每次作业都是留了一些出来，也听了同学说他们给未来可拓展性留的接口，而我留出来的接口是多变量，比如xyz同时出现以及指数上的表达式，但后来其实并没有考这些，唯一压中的是括号上的嵌套（，但不管怎么说，对项目的可拓展性上也是有了进一步的了解

还有就是每周Hack的过程真的感觉挺有趣的，个人感觉评测机的优势还是很明显的，相比于大数据连续跑，我感觉还是针对性+比较的方式的效果会好很多（其实我最开始就是用的前一种策略，但是总有同学的代码把我的评测机炮炸，比如输出过长，运算过慢等等，即使后面解决了这些评测机问题也还会出现有的bug会因为这部分的测试数据跳过而跳过了他们的bug），and Hack五个小时中18刀超过50%的正确率属实成就感满满了

最后在此感谢一下ysyxgg这一个月的交流and数据生成器，嘿嘿，懒人如我无疑了