OI 学习笔记:图论基础和树基础
图论基础 ofbwyx
本文根据 CC BY-NC-ND 4.0 进行许可,转载请务必标明出处。
图论基础
图论,解决在图上的一些问题。这一是个相对而言比较独立的模块,对其他算法的依赖较少。同时这也是一个普及组和提高组都可能有考的算法(甚至于 CSP-S 2022,四题中有三题是图论题)。因此学习一些图论知识很有必要。
本文将诠释一些概念,学习图的储存和遍历,以及图论中最基本的算法之一的拓扑排序。
前置知识:基本语法(包括结构体的使用),深搜,广搜。
图的重要概念
图,简单来说就是由边和点构成的图形。
某些概念可能不准确,请根据题目自行判断。
这是一些易燃枯燥无味的概念问题,建议先大致阅读一遍,遇到时再回来看。
边的方向
对于一条边,我们先考虑它的方向。有向边指有方向之分的边,无向边则没有方向。假设 \(u,v\) 之间有一条有向边,则可以从 \(u\) 到达 \(v\),反之不能到达。如果两点之间是无向边,则既可以从 \(u\) 到 \(v\),又可以从 \(v\) 到 \(u\)。
我们可以形象地把图看作城市的道路,有向边就是一条单行道,无向边就是双行道。
由有向边组成的图,我们成为有向图,由无向边组成的就是无向图。
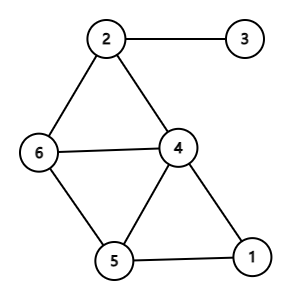
上图就是一张无向图,图上的边都是无向边。以结点 2 为例,从 2 出发可以到达结点 1、3、4、5、6。
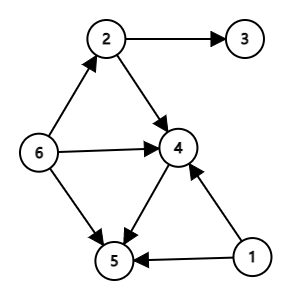
上图就是一张有向图图上的边都是有向边(方向即为箭头所指的)。同样以结点 2 为例,从 2 出发只能到达结点 3、4,无法到达其他结点。
路径和环
从一个点出发经过若干条边到达别的点,所经过的点就是一个途径(比较拗口也没啥用的定义)。
简单路径指没有重复经过的点和边的途径,简称为路径。简单来说,简单路径就是两点之间直接到达的路径,不能在同一个点或同一条边处绕圈圈(但不要求最短)。
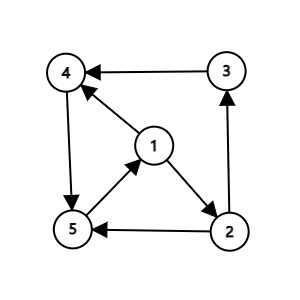
对于这张有向图,从 1 到 4 的简单路径有 \(1 \to 4\) 和 \(1 \to 2 \to 3 \to 4\)。其他的途径都会重复经过一些点或边,不属于简单路径。
环可以理解为首尾相接的简单路径(但是第一个和最后一个点是重合的,因此实际上环不是一条简单路径。这不是定义,仅供理解)。在上图中的环有三个,分别是 \(1 \to 2 \to 3 \to 4 \to 5 \to 1\)、\(1 \to 2 \to 5 \to 1\) 和 \(1 \to 4 \to 5 \to 1\)。
对于这张无向图,路径和环也有很多(随便拿手指比划两下都是),不再举例。
边的长度
边的长度,称之为边权。
路径或是环的长度就是其经过的边的边权之和。
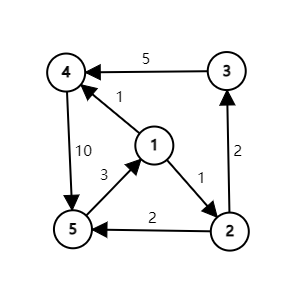
对于这张有边权的有向图,路径 \(1 \to 4\) 的长度为 \(1\),\(1 \to 2 \to 3 \to 4\) 的长度为 \(8\)。环 \(1 \to 4 \to 5 \to 1\) 的长度为 \(14\)。
无向图同理。
自环和重边
这两者是图中特殊的存在。自环指自己向自己连边(即存在 \(u \to u\))的途径。重边指图中有重复的边(如有向图中读入了不止一条 \(u \to v\),或是无向图中读入了不止一条 \(u \leftrightarrow v\)(有向图中的 \(u \to v\) 和 \(v \to u\) 属于两条不同的边))。
自环和重边在默认情况下是可以出现的,有时会影响某些算法。
入度和出度
一个点的入度就是以这个点为终点的边的数量,出度就是以这个点为起点的边的数量。点 u 的入度记为 \(d^-_u\),出度记为 \(d^+_u\)。
如果在一张图中只有环,那么对于图中任意一点 u,有 \(d^+_u = d^-_u = 1\),反之亦成立(自行思考)。
连通性问题
在一个无向图中,若从任意一点出发都可以到达其他所有点,则称这个图是一个连通图。一个点出发能到达的所有点组成的图的一部分称作连通块。
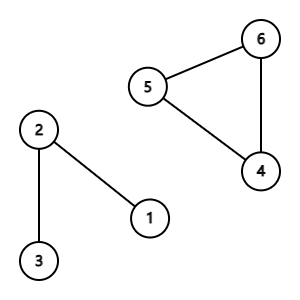
借助这个图感性理解一下:点 1,2,3 构成一个连通块,4,5,6构成另一个连通块。如果连上 \((1,5)\) 这条边,则这张图是一个连通图,有也是一个连通块。
在一个有向图中的连通性问题此处不展开讲述。
建图和遍历
解决图论问题,我们首先需要把图建出来,然后遍历从某个点出发能到达的所有点。
接下来的建图部分我们以这张图为例:
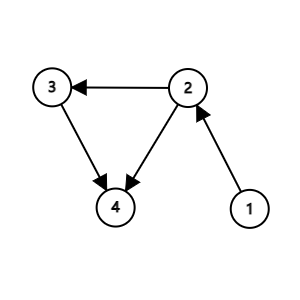
它的输入为(此处的输入格式:对于每行两个正整数 \(u,v\),有一条从 \(u\) 到 \(v\) 的有向边):
1 2
2 3
3 4
2 4
邻接矩阵
这是一种很好理解但是空间需求很大的建图方式,不常见但也需要学习。
我们创建一个二维数组,数组中储存两个点之间是否有边。
一开始所有点之间都没有连边,初始为 \(0\)。之后每连上一条边,我们就给对应的下标标为 \(1\)(对于无权图是这样的,有边权则一般需要存边权)。比如连了 \(1 \to 2\) 的边,那就把 \(f[1][2]\) 赋值为 \(1\)。依此类推,建图后的数组:
观察这个二维数组,第一维(竖下来的)1 到 4 分别对应着一条边的头,第二维对应边指向的点。数组中的值为 \(1\) 则表示这两个点之间有边。
若我们要遍历从点 \(u\) 出发能到达的其他点,那么我们就需要从 \(f[u][1]\) 枚举到 \(f[u][n]\),其中值为 \(1\) 的就是有连边的。例如从点 2 出发,我们发现 \(f[2][3],f[2][4]=1\),也就说明有 \(2 \to 3\) 和 \(2 \to 4\) 这两条边。代码如下:
// 邻接矩阵建图和访问
bool f[MAXN][MAXN];// 储存边的信息,MAXN 是最大点数
for(int i=1;i<=m;i++){// m 是边数
int u,v;
scanf("%d%d",&u,&v);
f[u][v]=1;// 连一条从 u 到 v 的边
}
for(int i=1;i<=n;i++){// n 是点数
if(f[u][i]){// 寻找一条从 u 出发的边
// 若条件为真进入 if,则说明有一条从 u 到 i 的边
;// 进行操作
}
}
邻接表
这是效率较高的一些建图方式的统称。
邻接矩阵储存了每个点连出去的边的信息,需要的空间很大,邻接表就可以很好地解决这一问题,利用动态大小的数组来存边。本节介绍通过动态数组 vector 建图的方法。
利用一个 vector,我们可以把从一个点出发能到达的所有边记录下来(也就相当于是邻接矩阵的第二维变为动态的,记下有连边的点的下标)。
定义 vector<int>v[MAXN],v[i] 中储存从结点 \(i\) 中出发可以到达的每个点的编号。第一条连的边是 \(1 \to 2\),那么我们就执行一个 v[1].push_back(2),也就是把结点 2 作为是从结点 1 出发可以到达的点。\(2 \to 3\) 就是 v[2].push_back(3),\(3 \to 4\) 就是 v[3].push_back(4),\(2 \to 4\) 就是 v[2].push_back(4)。
遍历同样简单,从 \(u\) 出发能到达的点就是 v[u] 中储存的点。比如对于结点 2,在 v[2] 中有两个元素分别是 3 和 4(进行了这两次的 push_back),因此有 \(2 \to 3\) 和 \(2 \to 4\) 这两条边。需要特别注意的是 vector 的第一个元素下标为 0。
代码如下:
// 邻接表建图和访问 1
vector<int>v[MAXN];
for(int i=1;i<=m;i++){
int u,v;
scanf("%d%d",&u,&v);
v[u].push_back(v);// 连一条从 u 到 v 的边
}
for(int i=0;i<v[u].size();i++){
// 有一条从 u 到 v[u][i] 的边
;// 进行操作
}
链式前向星
这是基于链表实现的邻接表,相较于 vector 的实现,效率更高(常数小),着重讲解。
用链式前向星建图有这样几个要点:
- 记录每条边的信息。
- 记录从每个点出发的边。
首先,我们定义一个结构体 edge 储存边的信息。由于我们只需要知道一条边连向哪里而不关注起点(下文会具体讲述原因),我们先把一条边的终点记录下来。
struct edge{
int v;
}e[MAXM];
把四条边的信息都先记录到结构体中,我们就完成了第一件事。数组中的信息是这样的:
- \(e[1].v=2\)
- \(e[2].v=3\)
- \(e[3].v=4\)
- \(e[4].v=4\)
接下来就需要记下从每个点出发有哪些边了。很容易可以想到用一个大数组或是 vector 存下由这个点出发的每条边,但这样就退化回了之前那两种见图方法了。我们在遍历图的时候肯定需要访问一个点出发的所有边,而且这些边的顺序是无关的——也就是说我们只需要做到顺序访问即可。
我们可以参考链表的思想:对于所有从同一个点出发的边,记录下第一条边和每条边的下一条边。这样我们就可以从这个点连的第一条边开始遍历所有连的边。
定义数组 head,\(head[i]\) 表示编号为 \(i\) 的点出发的第一条边。再在结构体中增加一个变量 \(nxt\) 储存这条边的下一条边。
struct edge{
int v,nxt;
}e[MAXM];
int head[MAXN];
再回顾我们的建图过程,建第一条边时候,它是从结点 1 出发的第一条边,下标为 1。除了上文的 \(u,v\) 之外,\(head[1]\) 需要赋值为 \(1\)。没有下一条边,\(nxt\) 仍为 \(0\)。第二、三条边同理。此时 \(head[1]=1,head[2]=2,head[3]=3\)。
接下来连的边是 \(2 \to 4\)。\(u,v\) 同上,但我们发现从结点 2 出发已经有一条 \(2 \to 3\) 了。按照之前的定义,我们需要把之前那条边的 \(nxt\) 变为新加的边的下标。但很容易发现这是一个效率极低的方法,因为我们不知道上一条边的下标,只能从第一条边开始遍历。
正难则反,因此我们更改一下定义。\(head[i]\) 定义为编号为 \(i\) 的点出发的最后一条边,\(nxt\) 表示这条边的上一条边。这样我们就可以在这条链的末尾很方便地加边了。前三条边没有任何改变(自行思考)。新加的 \(2 \to 4\) 的上一条边是 \(2 \to 3\),因此 e[4].nxt=2(4 是 \(2 \to 4\) 的编号而 2 是 \(2 \to 3\) 的编号,而在新边插入之前 \(2 \to 3\) 是从 2 出发的最后一条边,因此实际上此时 \(head[2]=2\)),head[i]=4(\(2 \to 4\) 成为了最后一条边)。
整理一下思路,加入一条新的边,我们需要把新边的前一条边指向旧边(即新边加入之前,从这一结点出发的最后一条边),然后把从这一结点出发的最后一条边编号变为新边。
由于我们可能不止需要连题目读入的边,因此我们再用一个变量 ecnt 来计数我们已经建了的边的数量。每次插入新边时就 ecnt++。代码如下:
// 链式前向星建图 1
struct edge{
int v,nxt;
}e[MAXM];
int head[MAXN],ecnt;
void build(int u,int v){// 用函数连边,连一条从 u 到 v 的边
e[++ecnt].v=v;// 边数 +1,储存边的终点
e[ecnt].nxt=head[u];// 新边的前一条边是原先的最后一条边
head[u]=ecnt;// 现在的最后一条边是新边
}
要进行遍历,我们需要像遍历链表一样从第一条(这里是最后一条)边出发,一条条遍历过去。对于结点 \(u\),从它出发的最后一条边就是 \(head[u]\)。需要注意第一条边的 \(nxt=0\),因为在它之前是没有边的。因此代码如下:
// 链式前向星访问 1
for(int i=head[u];i;i=e[i].nxt){
// 有一条从 u 到 e[i].v 的边
;// 进行操作
}
无向图和有权图的处理
我们拿一张无向有权图进行建图,加深一下印象邻接表和链式前向星的建图方法。
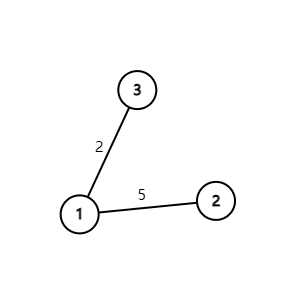
它的输入为(此处的输入格式:对于每行三个正整数 \(u,v,w\),表示有一条连接 \(u,v\) 的长度为 \(w\) 的无向边):
1 3 2
2 1 5
这次的图是无向图,不过对于连接 \(u,v\) 的无向边,我们可以看做 \(u \to v\) 和 \(v \to u\) 的两条边,建图方式就与上文所述的无异了。
不过这次多了一个边权的信息,我们需要将它也储存进去。
对于 vector 邻接表,我们可以新定义一个 vector<int>w[MAXN]。每一次新增一条边,我们就把它的边权信息也 push_back 到 w[u] 中。于是对于同一条边,它的终点和边权两个信息被分别存在了 v,w 的相同位置。如果有更多的边的信息只需要再定义新的数组即可。代码如下:
// 邻接表建图和访问 2
vector<int>v[MAXN],w[MAXN];
for(int i=1;i<=m;i++){
int u,v,ww;
scanf("%d%d",&u,&v,&ww);
v[u].push_back(v);// 连一条从 u 到 v 的边
w[u].push_back(ww);// 边的长度为 ww
}
for(int i=0;i<v[u].size();i++){
// 有一条从 u 到 v[u][i] 的边
// 这条边的长度为 w[u][i]
;// 进行操作
}
而对于链式前向星也是同样的,在结构体中新增一个数据即可,访问时也是这样。
// 链式前向星建图和访问 2
struct edge{
int v,w,nxt;
}e[MAXM];
int head[MAXN],ecnt;
void build(int u,int v,int w){// 用函数连边,连一条从 u 到 v 的边,长度为 w
e[++ecnt].v=v;// 边数 +1,储存边的终点
e[ecnt].w=w;// 边的长度为 w
e[ecnt].nxt=head[u];// 新边的前一条边是原先的最后一条边
head[u]=ecnt;// 现在的最后一条边是新边
}
for(int i=head[u];i;i=e[i].nxt){
// 有一条从 u 到 e[i].v 的边
// 边的长度为 e[i].w
;// 进行操作
}
比较
三种方式各有优缺点,进行一下比较。
建图所用的空间,邻接矩阵是最大的(因此只能用于建一些有特殊需求的较小的图),理论上链式前向星的空间会大于邻接表(需要多储存一个 nxt 信息),但由于 vector 的问题,实际上很多时候邻接表反而会用更大的空间(不过无关紧要,很少会有题目卡这种东西)。
因此我们更关心的是时间问题。每连一条边,三种方法都是常数复杂度的,差异主要在于访问上。记从一张图的点数为 \(n\),边数为 \(m\),结点 u 为起点的边的数量为 \(d^+_u\),则:
- 遍历从结点 u 出发的所有边:邻接矩阵 \(O(n)\),后两者 \(O(d^+_u)\);
- 遍历整张图(利用下文所述的深广搜):邻接矩阵 \(O(n^2)\),后两者 \(O(n + m)\);
- 查询从结点 u 出发是否有到达 v 的边:邻接矩阵 \(O(1)\),后两者 \(O(d^+_u)\),按点编号排序过的邻接表 \(O(\log(d^+_u))\)。
因此邻接矩阵在查询边是否存在这一方面特别迅猛,但无奈它的空间需求太大了。邻接表优势在于可以把从同一个点出发能到达的点按照编号排序。链式前向星则由于其边有编号,在一些特殊场景下有应用。平时做题时建议在后两者中选取自己喜欢的。
在接下来的部分,部分代码将会有邻接表版本的和链式前向星版本的,但一些可能只有链式前向星版本(我习惯这么写)。
深搜和广搜
遍历一个图,常用的方法是深搜或广搜。与平时的深广搜类似但不完全相同。
在图论中,深搜和广搜在大部分情况下无法互相替代。
深搜
深搜就是通过函数递归(自身调用自身)实现对图的遍历。
我们从一个点出发,遍历这个点出发的所有边,然后调用自身访问每条边所连的终点,如此反复。为了防止重复访问一些点,我们需要对访问过的点打一个标记,再次访问到的时候不往这个点搜。
根据这个思路,我们便可以先写出一个伪代码:
dfs(u)
u 访问过,打上标记
遍历所有 u 出发的边(能到达的点)v
如果 v 没有标记
dfs(v)
定义数组 vis[MAXN] 储存这个标记,我们便可以实现代码了:
// 邻接表 dfs
int vis[MAXN];
void dfs(int u){
vis[u]=1;
for(int i=0;i<v[u].size();i++){
if(!vis[v[u][i]])dfs(v[u][i]);
}
}
// 链式前向星 dfs
int vis[MAXN];
void dfs(int u){
vis[u]=1;
for(int i=head[u];i;i=e[i].nxt){
if(!vis[e[i].v])dfs(e[i].v);
}
}
而在深搜过程中对点或边的信息的维护,则根据具体需求写在 for 之前或 if 前后。
广搜
广搜就是用一个数据结构(常用队列)存下这一轮要处理的结点,然后进行处理并将新的结点入队,直到队列空。
我们将出发时的点入队,然后开始循环:取出对头的点,遍历这个点出发的所有边,然后将每条边所连的终点入队。同样的给访问过的点打标记,如果访问过则不入队。
根据此思路写出伪代码:
将起点入队
起点标记为访问过
while(队列不为空)
取出队头 u
遍历所有 u 出发的边(能到达的点)v
如果 v 没有标记
v 入队
v 标记为访问过
定义 vis[MAXN],实现代码:
// 邻接表 bfs
int vis[MAXN];
queue<int>q;
void bfs(){
q.push(1);// 此处写的是从结点 1 开始
vis[1]=1;
while(!q.empty()){
int u=q.top();
q.pop();
for(int i=0;i<v[u].size();i++){
if(!vis[v[u][i]]){
q.push(v[u][i]);
vis[v[u][i]]=1;
}
}
}
}
// 链式前向星 bfs
int vis[MAXN];
queue<int>q;
void bfs(){
q.push(1);// 此处写的是从结点 1 开始
vis[1]=1;
while(!q.empty()){
int u=q.top();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
同样的,操作应写在适当位置。
例题:求连通块点权和
简要题意:给定一个无向无权图,图上每个点都有一个权值。给定一个结点,询问这个结点所在的连通块的点权和。
分析:求连通块内的点权和,我们只需要从这个点出发进行搜素,把访问到的所有点点权加上即可。因为能访问到的点都是互相连通的,即都在这个连通块内。至于搜索的方法,深搜和广搜均可(这其实是图论题中少有的深广搜二者都能达到目的的题目)。
实现:定义数组 a[MAXN] 从数据读入点权,ans 统计答案。先读入数据,建图,然后对这个图进行深搜或广搜,在搜到一个新的结点时 ans+=a[u] 进行答案的统计。
代码:
// 链式前向星 dfs
int vis[MAXN],ans;
void dfs(int u){
ans+=a[u],vis[u]=1;
for(int i=head[i];i;i=e[i].nxt){
if(!vis[e[i].v])dfs(e[i].v);
}
}
例题:统计连通块个数
简要题意:给定一个无向无权图,统计图里有几个连通块。
分析:在对图进行搜索的时候我们会对访问的点打上一个标记,我们可以利用这个标记进行统计。从第一个点出发进行一次搜索,所有打了标记的点都是与结点 1 在同一个连通块内的了。接下来寻找没有标记的点——也就是不在这个连通块内的点——出发进行搜索,每找到一个就把答案加一。
实现:遍历一遍所有点,只要没有标记的就以它为起点出发搜索,并且答案加一。
代码:
// 链式前向星 bfs
int vis[MAXN],ans;
queue<int>q;
void bfs(int r){
q.push(r);
vis[r]=1;
while(!q.empty()){
int u=q.top();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
int main(){
for(int i=1;i<=n;i++)if(!vis[i])bfs(i),ans++;
}
拓扑排序
用途
每个算法都有其前置知识,比如拓扑排序的前置知识有建图和搜索。同时,不可能存在算法 A 前置为 B,而 B 的前置又有 A(那就没法正常学了)。我们把每个算法作为一个结点,从其前置知识出发向它连边,我们便得到了一张有向无环图。拓扑排序就是在这张图上找一个合理的顺序,在学习每一个新知识时都学习过它的前置知识——也就是对这张图进行排序。
抽象来说,将一张图的点排序使其每个点所依赖的点都在它之前,这个过程就是拓扑排序。
做法
用一个数组记录下每个点的入度,也就是这个点依赖的点的个数。每个点依赖的点都要在它之前,那么第一个点必须要没有依赖的点,也就是入度为 0。
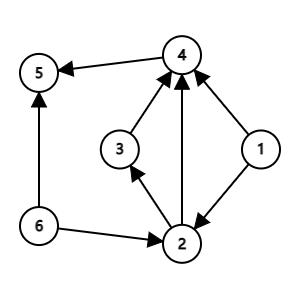
在这张图中,我们可以发现结点 1 和 6 都是没有依赖的,于是我们可以先确定这两个点的顺序(至于这两点之间的顺序实际上是没有差别的,因为题目要么是要求算数值,要么会有 SPJ)。那么,以这两个点为依赖的点就少了一个依赖了(因为这两点已经在它们之前了)。于是就形成了这样一张新的图:
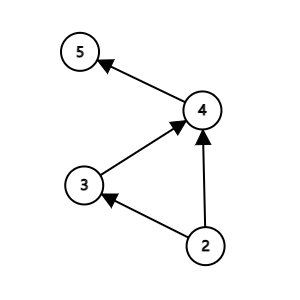
我们发现结点 2 也没有依赖的了,那就对它再进行一次这样的操作,然后就剩 \(3 \to 4 \to 5\),最终结果也就显而易见了。
再重新观察一开始的图:\(d^-_1 = d^-_6 =0\),而 \(d^-_2 = 2\)。在排序了结点 1 和 6 之后,2 的两个依赖都被排序了,于是在新图中 \(d^-_2 = 0\),就可以作为新的起点开始遍历。
整理一下思路:从入度为 0 的结点开始逐个遍历这个点出发的所有边,把到达的点的入度减一,然后将入度为 0 的点也进行遍历,直到整个图排序完。使用一个队列维护需要遍历的点。
将所有入度为 0 的点入队
while(队列不为空)
取出队头 u
将 u 放进排序好的序列(按题目需求)
遍历所有 u 出发的边(能到达的点)v
v 的出度 -1
如果 v 的出度为 0
将 v 入队
为什么我们不用在这个广搜中判断结点是否访问过?一方面,当一个结点入度不为零时,它会被多次访问,每次入度减一,直到为零。另一方面,当其入度为零后,它会被放进队列,从它出发遍历其他边,此时已经没有边指向它了,因此也不会被重复访问。
例题:[NOIP2020] 排水系统
简要题意:给定一个有向无环图,\(1,2,\dots,m\) 结点各有一个单位的污水,会均匀流向其他结点,没有向这些点连的管道。没有出边的结点会汇集污水,求这些结点各有多少污水。(本题有点阅读理解的味道,建议自行阅读原题面理解意思)
完整题面请见 https://www.luogu.com.cn/problem/P7113。
分析:对于每个结点,在它的水流向其他结点之前,别的水必须先流到它这里,于是就出现了这样一个顺序问题。在有向无环图上的顺序问题,我们就应该想到拓扑排序。我们用一个数组 a[MAXN] 记录此结点现在有多少污水,在遍历每个结点时把它的污水平均分给以它为起点的边所连的点。最后把没有出边的点的污水输出即为答案。
实现:建图并记录入度出度,拓扑排序,将出度为零的点的污水量输出。注意一些小细节,比如输入的格式,要写一个分数加法,还要写一个高精度(不过,从 2021 年开始允许在此类比赛中使用 __int128 了,可以免去高精度)。
代码:
// 排水系统
#include<bits/stdc++.h>
#define int __int128// long long 也会炸,用这个代替手写高精度(考场能用)
using namespace std;
int read(){
int w=0,ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-48,ch=getchar();
return w;
}
void put(int x){
if(x>9)put(x/10);
putchar(x%10+48);
}// __int128 需要自己手写读写
#define MAXN 100003
int n,m,ap[MAXN],aq[MAXN];
int in[MAXN],out[MAXN];
queue<int>q;
struct edge{
int v,nxt;
}e[MAXN*5];
int head[MAXN],ecnt;
void build(int u,int v){
e[++ecnt].v=v;
e[ecnt].nxt=head[u],head[u]=ecnt;
}
void pls(int p1,int q1,int p2,int q2,int& ansp,int& ansq){
int tp=p1*q2+p2*q1,tq=q1*q2,tmp=__gcd(tp,tq);
ansp=tp/tmp,ansq=tq/tmp;
}// 分数加法
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++){
aq[i]=1;// 分母为 1
if(i<=m)ap[i]=1;// 前 m 个一开始就有水
int t=read();
while(t--){
int v=read();
build(i,v);
in[v]++,out[i]++;
}
}// 读入边,建图,记录出入度
for(int i=1;i<=m;i++)q.push(i);// 前 m 个点是没有入边的
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
pls(ap[u],aq[u]*out[u],ap[v],aq[v],ap[v],aq[v]);// 流水
in[v]--;// 入度减一
if(!in[v])q.push(v);// 如果入度为 0 则入队
}
}// 拓扑排序
for(int i=1;i<=n;i++)if(!out[i]){
put(ap[i]),putchar(' ');
put(aq[i]),putchar('\n');
}
return 0;
}
杂项
反图
反图是在有向图中的概念。把一张图的所有边连反得到的图就是反图(例如对于只有 \(u \to v\) 这一条边的图,那么只有 \(v \to u\) 这一条边的图就是前者的反图)。在一些情况下我们可能需要在对原图进行操作后再对其反图进行操作。很多时候我们可以再建一个图,但本小节有关如何 优雅地 在原图上建反图。
对于邻接表,由于其自身特性,似乎无法简单地在原图上建反图。邻接矩阵略。
对于链式前向星,我们则需要在一开始建图时就存下边的起点 u。在建反图的过程中,我们直接遍历所有的边,将它的 \(u\) 和 \(v\) 互换。不过我们还需要处理 head 数组和 nxt。旧的 head 数组已经没用了,因此我们要先清零它。接下来就像正常建图一样,每条边正常处理 head 和 nxt 即可。代码如下:
// 链式前向星建反图
for(int i=1;i<=n;i++)head[i]=0;
for(int i=1;i<=ecnt;i++){
swap(e[i].u,e[i].v);
e[i].nxt=head[e[i].u],head[e[i].u]=i;
}
为什么没考虑自环重边
在 dfs 和 bfs 时,我们没有对自环和重边进行特判。这是因为对于自环 \(u \to u\),在访问到的时候已经对这个点打上了标记,走这条边会因为有标记而不再访问这一点。重边也是如此。
树基础
图论中的树,是图的特殊形态。它形似倒挂的树(根在上叶子在下)而得名。

本文将诠释一些概念,学习一些基本内容,如何求树的直径,以及通过倍增求树上两点的最近公共祖先。
前置知识:图论基础,倍增。
树的重要概念
树的定义
我们称一个有 \(n\) 个结点,\(n-1\) 条边的无向连通图为树。我们也可以定义一个无向无环的连通图就是树,或定义任意两个结点之间有且仅有一条简单路径的无向图为树。这样定义出的树是一棵无根树。定义一个结点为树的根结点,那么这棵树就是一颗有根树了。
有根树中的定义
我们将一棵有根树以根结点在最上的顺序画出:
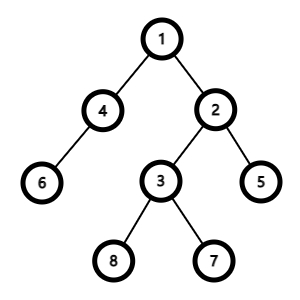
这棵树可以长成这样,它的根结点为 1。对于根结点之外的结点,与它相邻的点中比它更靠近根结点的是它的父亲(准确而言,一个点的父亲是从该点到根路径上的第二个结点)。例如,结点 2 的父亲是 1,结点 6 的父亲是 4。一个结点到根路径上除了自己的所有结点称为它的祖先,例如结点 8 的祖先有 1、2、3,结点 4 的祖先有 1。根结点没有父亲。
如果 u 是 v 的祖先,那么 v 是 u 的子结点。一个结点的子结点和子结点的子结点是它的后代。例如结点 2 的子结点有 3、5,后代有 3、5、7、8。
一个结点的子结点互为兄弟,如 3、5。
结点到根结点路径上的边数是它的深度,树所有结点深度的最大值是树的高度。如结点 3 的深度为 2,结点 7 的深度为 3,这棵树的高度为 3。
一个结点的子树是以这个结点为根的树,也就是删去它与它父结点的边后剩下的树。
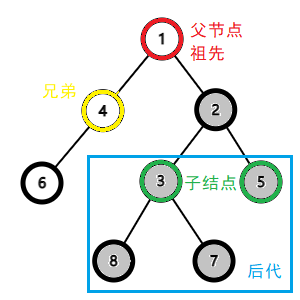
这是与结点 2 相关的结点情况。底色为灰的结点就是 2 的子树。
建树
只记录父结点
一种非常简单的建树方法,记录下每个结点的父结点。用于只需要从子结点到父结点的递推问题。
代码略。
邻接表
我们可以直接把树当作无向图来存储,代码略。
此处邻接表包括 vector 实现的邻接表和链式前向星。
遍历树
基本做法
对树的遍历主要是通过深搜实现(广搜也是可以的)。
与图的深搜不同,树上深搜不需要记录一个结点是否被访问过,但需要在搜索时额外传入一个信息 fath 表示这个结点的父结点,随后遍历这个点出发的边时跳过连向父结点的边。不过如果已经处理出了每个点的父结点,则不需要传入 fa,改为 if(v==fa[u])continue;。
代码:
// 树的深搜
void dfs(int u,int fath){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fath)continue;// 不遍历父结点
dfs(v,u);// 子结点的父结点是它自己
}
}
int main(){
dfs(1,0);// 根结点的父结点是 0(此处令根结点为 1)
}
信息维护
在对树进行搜索时,我们需要按需维护一些信息以供接下来的解决问题使用。常见的信息有:结点的父结点 fa,深度 dep,子树大小 siz。
父结点的维护很简单,在搜到时候记下 fa[u]=fath 即可。至于深度,我们可以简单地发现一个点的深度比它的父结点多一,因此搜到一个结点时候 dep[u]=dep[fath]+1 即可。
结点 u 的子树大小就是它所有子结点的子树大小加一(因为子树就是以自己为根,自己和子结点组成的树),因此我们可以将 siz 初始化为 1,然后在遍历 u 的每个子结点后将 u 的子树大小加上这个子结点的子树大小。
代码:
// 树的深搜 信息维护
void dfs(int u,int fath){
fa[u]=fath,dep[u]=dep[fath]+1;// 父结点和深度
siz[u]=1;// 子树大小初始化为 1
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fath)continue;
dfs(v,u);
siz[u]+=siz[v];// 加上这个子结点的子树大小,注意这句要写在 dfs 之后
}
}
树的直径
树上距离最远两点之间的距离是树的直径。树的直径可能不止一条。
例如在上面的树上,直径有两条,分别是 \(6-4-1-2-3-8\) 和 \(6-4-1-2-3-7\)。
两次 dfs
这种方法仅适用于边权不为负的情况!
我们从任意一个点进行搜索,求出距离这个点最远的点,记为 p。接下来再从 p 开始进行一次搜索,求出距离 p 点最远的点 q,则 p 和 q 两点间的路径就是树的直径。
证明思路:以后再补。
代码:
// dfs 树的直径
int p,dis[MAXN];
void dfs(int u,int fath){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fath)continue;
dis[v]=dis[u]+1;// 距离根结点的距离(也可以理解为深度)
if(dis[v]>dis[p])p=v;// 记录最深的深度
dfs(v,u);
}
}
int main(){
dfs(1,0);// 随便取一个点为根进行深搜,执行完后 p 就是距离最远的,是直径的一端
dfs(p,0);// 再寻找距离 p 最远的点记为 p',是直径的另一端
}
如果要记录下这条直径,则可以在第二次 dfs 时候记录下每个结点的父结点(以第一次 dfs 得出的 p 为根的树上),最后从树的直径的另一端 p' 开始一路回到 p 即为整条直径了。
如果树的边有权值,则 dfs 中的 dis[v]=dis[u]+1 要改为 dis[v]=dis[u]=e[i].w(因为实际上对于没有权值的边,默认长度都为 1)。
时间复杂度为 \(O(n)\)。
树形 dp
树形 dp 可以正确地处理负边权。
我们记录下以 1 为根时从每个点出发能到达的最远和次远结点距离,树的直径就是每个结点的两个值相加的最大值。
树形 dp 一般来说是通过递归实现的(也就是记忆化搜索),代码如下:
// dp 树的直径
int d1[MAXN],d2[MAXN],ans;
void dfs(int u,int fath){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v,tmp;
if(v==fath)continue;
dfs(v,u);
tmp=d1[v]+1;// 1 是边权
if(tmp>d1[u])d2[u]=d1[u],d1[u]=tmp;// 如果这个往子结点能到达最远的点
else if(t>d2[u])d2[u]=t;// 如果能到达次远的点
}
ans=max(ans,d1[u]+d2[u]);// 记录答案
}
记录路径的方法,可以记录下 dp 过程中每个点最远和次远结点的子结点编号,然后找到最远和次远这两条链的交点(也就是直径上的某一点),再从这个点出发向最远和次远结点得到整条路径。
时间复杂度为 \(O(n)\)。
定理和性质
在树上从任意结点开始进行一次 dfs,到达的距离其最远的结点必为直径的一端。
若树上所有边边权均为正,则树的所有直径中点重合。
证明省略(以后再补)。
最近公共祖先
定义和性质
最近公共祖先(LCA)指树上两点的公共祖先中离根结点最远的一个。
对于树上两点 \(u,v\),记他们的最近公共祖先为 \(\text{LCA}(u,v)\):
若 \(u\) 是 \(v\) 的祖先:\(\text{LCA}(u,v)=u\),否则两位于 \(\text{LCA}(u,v)\) 的不同子树中。两点最近公共祖先必然在两点间最短路上。
记结点 \(u\) 到树根的距离为 \(h(u)\),则 \(u,v\) 两点间距离为 \(h(u)+h(v)-h(\text{LCA}(u,v))\)。
做法
求 LCA 的方法有非常多,本节讲解倍增的方法。
我们可以很简单地想出一种朴素的方法:先将两个点跳到同一深度,再从两个点出发分别向它们的父结点跳,直到跳到的同一个点。不过这种方法的时间复杂度是较高的,因此我们需要对其进行优化。
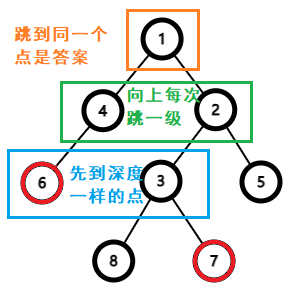
我们使用倍增这种方法进行优化:记 \(fa_{x,i}\) 为结点 \(x\) 的第 \(2^i\) 个祖先 ,先预处理求出所有点的 \(fa_{x,i}\),接下来用与朴素解法类似的方法,先将两个点跳到同一深度,然后开始一起向祖先跳,每次跳 2 的若干次方级。因此我们只需要将结点的每个 \(2^i\) 级祖先都尝试一遍就可以得出答案了。
如果能理解倍增的想法,应该能够理解这种做法。不是很懂?树链剖分欢迎你。
代码:
// 倍增 LCA
#include<bits/stdc++.h>
using namespace std;
inline int read(){
int w=0,ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9'){
w=w*10+ch-48;
ch=getchar();
}
return w;
}
#define MAXN 500005
int n,m,s;
struct edge{
int v,nxt;
}e[MAXN<<1];
int head[MAXN],ecnt=0;
void build(int u,int v){
e[++ecnt].v=v;
e[ecnt].nxt=head[u],head[u]=ecnt;
}
int fa[31][MAXN],dep[MAXN];// 祖先和深度的预处理
void dfs(int now,int fath){
fa[0][now]=fath,dep[now]=dep[fath]+1;
for(int i=1;i<31;i++)fa[i][now]=fa[i-1][fa[i-1][now]];
for(int i=head[now];i;i=e[i].nxt)
if(e[i].v!=fath)dfs(e[i].v,now);
}// 通过 dfs 预处理出每个点的 2^i 级祖先
int lca(int x,int y){
if(dep[x]>dep[y])swap(x,y);// 使 y 是深度最深的
for(int i=30;i>=0;i--)
if(dep[fa[i][y]]>=dep[x])y=fa[i][y];// 使两点深度相同
if(x==y)return x;// 如果 x 是 y 的祖先直接返回答案
for(int i=30;i>=0;i--)
if(fa[i][x]!=fa[i][y])x=fa[i][x],y=fa[i][y];// 一起向上跳直到两点为同一点
return fa[0][x];// 此时即为答案
}
int main(){
n=read(),m=read(),s=read();
for(int i=1;i<n;i++){
int x=read(),y=read();
build(x,y),build(y,x);
}
dfs(s,0);
while(m--){
int x=read(),y=read();
printf("%d\n",lca(x,y));
}
return 0;
}
例题:猴皮面包树
完整题面:YAOI Round #26 (Div.1+Div.2) F. 猴皮面包树 - 福州延安中学 OJ 或 U248852 YAOI Round #26 (Div.1+Div.2) F. 猴皮面包树 - 洛谷(数据不完整)。
简要题意
给定一棵树的根结点和有连边的点的编号(但不知道哪个点是父结点,也就是说输入的 u,v 可能是 u 为 v 的父结点,也可能相反)。询问一些点的父结点编号、深度、距离它最远的结点编号、子树大小。
分析
由于已知树的根结点,我们可以从根结点出发向下进行一次深搜,便可处理出每个点的父结点、深度和子树大小了。这是简单的。
求距离最远的结点编号,一个容易想到的方法是从这个点出发进行深搜,但这种做法是低效的。这时我们需要用到一个重要性质:在树上从任意结点开始进行一次 dfs,到达的距离其最远的结点必为直径的一端。
因此我们在 dfs 中求出树的直径的两端,再预处理出这两个端点到树上每一点的距离(一共是三次深搜,第一次处理基本信息和直径一端,第二次求到直径一端的距离和直径的另一端,第三次求距离)。查询时候只需要把两个距离比较取最大就可以了。
此外需要注意一个细节:在处理两个距离时要 dis[0]=-1,因为一个结点到自己的距离为 0,但深搜起始点的距离会被赋值为 dis[0]+1。
代码
// 猴皮面包树
#include<bits/stdc++.h>
using namespace std;
int read(){
int w=0,ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-48,ch=getchar();
return w;
}
#define MAXN 1000003
int n,r,q;
int fa[MAXN],dep[MAXN],siz[MAXN];
int p1,p2,dis1[MAXN],dis2[MAXN];
struct edge{
int v,nxt;
}e[MAXN<<1];
int head[MAXN],ecnt;
void build(int u,int v){
e[++ecnt].v=v;
e[ecnt].nxt=head[u],head[u]=ecnt;
}
void dfs1(int u,int fath){
fa[u]=fath,dep[u]=dep[fath]+1,siz[u]=1;// 维护三个数据
if(dep[u]>dep[p1])p1=u;// 求出直径一端
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fath)continue;
dfs1(v,u);
siz[u]+=siz[v];// 求子树大小
}
}
void dfs2(int u,int fath){
dis1[u]=dis1[fath]+1;// 求第一个距离
if(dis1[u]>dis1[p2])p2=u;// 求出直径另一端
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fath)continue;
dfs2(v,u);
}
}
void dfs3(int u,int fath){
dis2[u]=dis2[fath]+1;// 求第二个距离
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fath)continue;
dfs3(v,u);
}
}
int main(){
n=read(),r=read(),q=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
build(u,v),build(v,u);
}
dis1[0]=dis2[0]=-1;// 细节
dfs1(r,0),dfs2(p1,0),dfs3(p2,0);
while(q--){
int op=read(),x=read();
if(op==1)printf("%d\n",fa[x]);
else if(op==2)printf("%d\n",dep[x]);
else if(op==3)printf("%d\n",max(dis1[x],dis2[x]));
else printf("%d\n",siz[x]);
}
return 0;
}
最小生成树
一张图的生成图满足结点是原图的所有结点、边都是原图中的部分边。为树的生成图称为生成树。一张图边权和最小的生成树即为最小生成树。
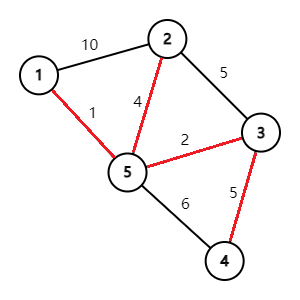
图中红色边构成的树就是这个图的最小生成树。它联通了整个图并且满足边权最小。
常见求最小生成树的算法有 Kruskal、Prim 等。
Kruskal
这种求最小生成树的算法基本思想是贪心:我们将边权排序,从小到大遍历每条边,如果这条边所连的两个点不连通,则将这条边作为最小生成树的一边,当所有点联通后便形成了一棵最小生成树。维护若干个点是否连通可以通过并查集实现。证明省略,可以查阅 OI-Wiki 上的证明。
时间复杂度为 \(O(m \log m)\)。
代码:
// 最小生成树
#include<bits/stdc++.h>
using namespace std;
int read(){
int w=0,ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')w=w*10+ch-48,ch=getchar();
return w;
}
#define MAXN 5005
#define MAXM 200005
int n,m,ans=0,cnt=0;
struct edge{
int u,v,w;
}e[MAXM];
int f[MAXN];
int find(int x){
if(f[x]==x)return x;
return f[x]=find(f[x]);
}
bool cmp(edge a,edge b){
return a.w<b.w;
}
int main(){
n=read(),m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read(),z=read();
e[i].u=x,e[i].v=y,e[i].w=z;
}
for(int i=1;i<=n;i++)f[i]=i;
sort(e+1,e+1+m,cmp);
for(int i=1;i<=m;i++){
int u=find(e[i].u),v=find(e[i].v);
if(u==v)continue;
f[u]=v,ans+=e[i].w,cnt++;
if(cnt==n-1)break;
}
if(cnt!=n-1)puts("orz");
else printf("%d",ans);
return 0;
}
Prim
这种方法是从每个点出发寻找与它距离最小的点,与最短路算法 Dijkstra 类似。这也需要数据结构(一般是堆)进行优化。
二叉堆优化的 Prim 时间复杂度为 \(O((n+m) \log n)\),在边较多的稠密图中复杂度优于 Kruskal,但常数较大,实际上不一定跑得快。
具体实现略去,可以参考 Dijkstra。以后再补。
本文参考资料:
- 图论 - OI Wiki
- 树基础 - OI Wiki
- NormanWang 的博客
- 《算法竞赛进阶指南》
水平所限,若有错误或讲述不清处请指出,谢谢。
ofbwyx

