【质量估计融合进分类分支+回归分支建模为一般分布】Generalized Focal Loss（GFL）论文精读

原始题目：Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection
中文翻译：Generalized Focal Loss：学习用于密集目标检测的 Qualified and Distributed Bounding Boxes
发表时间：2020年6月8日
平台：arxiv
来源： 南京理工-李翔
文章链接：https://arxiv.org/abs/2006.04388
开源代码：https://github.com/implus/GFocal

摘要

• One-stage detector 基本上将目标检测表述为 dense classification and localization(bounding box regression)。
• The classification 通常采用 Focal Loss来优化，the box location 通常采用 Dirac delta distribution 来学习。
• one-stage detectors 最近的一个趋势是 引入 一个单独的预测分支 来估计定位的质量，其中预测的质量有利于分类，从而提高检测性能。
• 本文探讨了上述三个基本 elements 的表示: quality estimation, classification and localization。
• 在现有的实践中发现了两个问题:
  • (1) 训练和推理之间的 the quality estimation 和分类 的使用不一致(即分开地训练，但在测试中组合使用);
  • (2) 在复杂场景中存在歧义性和不确定性时，用于定位的 Dirac delta分布 不灵活，这是常见的情况。

问题1:
(1) 用法不一致。训练的时候，分类和质量估计各自训自己的，但测试的时候却又是乘在一起作为 NMS score 排序的依据，这个操作显然没有 end-to-end，必然存在一定的 gap。
(2) 对象不一致。借助 Focal Loss 的力量，分类分支能够使得少量的正样本和大量的负样本一起成功训练，但是 质量估计通常就只针对正样本训练。那么，对于 one-stage 的检测器而言，在做 NMS score 排序的时候，所有的样本都会将 分类score 和 质量预测score相乘 用于排序，那么必然会存在一部分分数较低的“负样本”的质量预测是没有在训练过程中有监督信号的，也就是说 对于大量可能的负样本，他们的质量预测是一个未定义行为(因为质量估计只针对正样本)。这就很有可能引发这么一个情况：一个 分类score相对低的真正的负样本，由于预测了一个不可信的极高的质量 score，而导致它可能排到一个真正的正样本（分类score不够高且质量score相对低）的前面。
见 图1 a.

对于问题一：为了保证 training 和 test 一致，同时还能够兼顾 分类score 和 质量预测score 都能够训练到所有的正负样本，那么一个方案呼之欲出：就是将两者的表示进行联合。这个合并也非常有意思，从物理上来讲，我们依然还是保留分类的向量，但是对应类别位置的置信度的物理含义不再是分类的score，而是改为质量预测的score。这样就做到了两者的联合表示，同时，暂时不考虑优化的问题，我们就有可能完美地解决掉第一个问题。

问题2:
在复杂场景中，边界框的表示具有很强的不确定性，而现有的框回归本质都是建模了非常单一的狄拉克分布，非常不 flexible。我们希望用一种 general 的分布去建模边界框的表示。如 图3.被水模糊掉的滑板，以及严重遮挡的大象。

对于问题二，我们选择直接回归一个任意分布来建模框的表示。当然，在连续域上回归是不可能的，所以可以用离散化的方式，通过 softmax 来实现即可。这里面涉及到如何从狄拉克分布的积分形式推导到一般分布的积分形式来表示框，详情可以参考原论文。

为了解决这些问题，我们为这些 elements 设计了新的表示形式。

• 具体来说，我们将 the quality estimation 合并到 the class prediction vector 中，形成 localization quality and classification 的联合表示，并使用一个向量来表示 box locations 的任意分布。
• 改进后的表示消除了不一致的风险，准确地描述了真实数据中的灵活分布，但包含连续的标签，这超出了 Focal Loss 的 scope。

然后，我们提出 广义焦点损失( Generalized Focal Loss (GFL))，将 Focal Loss 损失从离散形式推广到连续形式，以成功优化。

在COCO测试开发中，GFL 使用 ResNet-101 backbone 实现了45.0%的 AP，超过了最先进的 SAPD(43.5%)和ATSS(43.6%)，在相同的 backbone 和训练设置下，具有更高或相当的推理速度。值得注意的是，我们最好的模型可以在单个 2080Ti GPU上以 10 FPS 实现48.2%的 a single-model single-scale AP。

1. 引言

近年来，dense detectors 逐渐引领了目标检测的潮流，而对 bounding boxes and their localization quality estimation 表示的关注也带来了令人鼓舞的进步。

具体来说， bounding box representation 被建模为一个简单的 Dirac delta distribution[10,18,32,26,31]，这在过去的几年里被广泛使用。

正如在FCOS[26]中宣传的那样，当在推理过程中将 the quality estimation 与 classification confidence 相结合(通常 multiplied) 作为 Non-Maximum Suppression (NMS) 排序过程的最终分数[12,11,26,29,35]时，预测 an additional localization quality (例如 IoU score [29] or centerness score [26] )会带来检测精度的一致提高。尽管他们取得了成功，但我们在现有实践中观察到以下问题:

Inconsistent(不一致) usage of localization quality estimation and classification score between training
and inference:

图1: 分类和定位质量估计的现有分开表示与提出的联合表示的比较。(a):Current practices [12, 26, 29, 35, 31] for the separate usage of the quality branch (i.e., IoU or centerness score) during training and test. (b): Our joint representation of classification and localization quality enables high consistency between training and inference.

• (1) 在最近的 dense detectors 中，the localization quality estimation and classification score 通常是独立训练的，但在推理过程中被综合利用(例如 multiplication)[26,29] (图1(a));

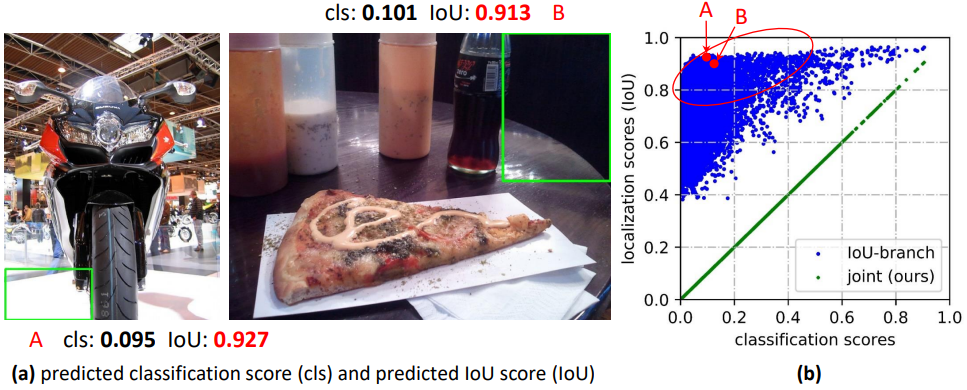
Figure 2: 不可靠的 IoU predictions of current dense detector with IoU-branch.

• (a): We demonstrate some background patches (A and B) with extremely high predicted quality scores (e.g., IoU score > 0.9), based on the optimized IoU-branch model in 图 1(a).
  The 散点图 in (b) denotes the 随机抽样实例 with their predicted scores, where the blue points clearly illustrate the weak correlation between predicted classification scores and predicted IoU scores for separate representations. 红圈中的部分包含许多可能的 negatives with large localization quality predictions，这些 negatives 可能排在 true positives 之前，从而损害性能。相反，我们的联合表示(绿色点)迫使它们相等，从而避免了这种风险。

• (2) the localization quality estimation 的监督目前只分配给正样本[12,11,26,29,35]，这是不可靠的，因为负样本可能有机会获得不受控制的更高质量的预测(图2(a))。

这两个因素会导致训练和测试之间的差距，并可能降低检测性能，例如，在 NMS 期间，negative instances with randomly high-quality scores 可能排在 positive examples with lower quality prediction 之前。

Inflexible representation of bounding boxes:

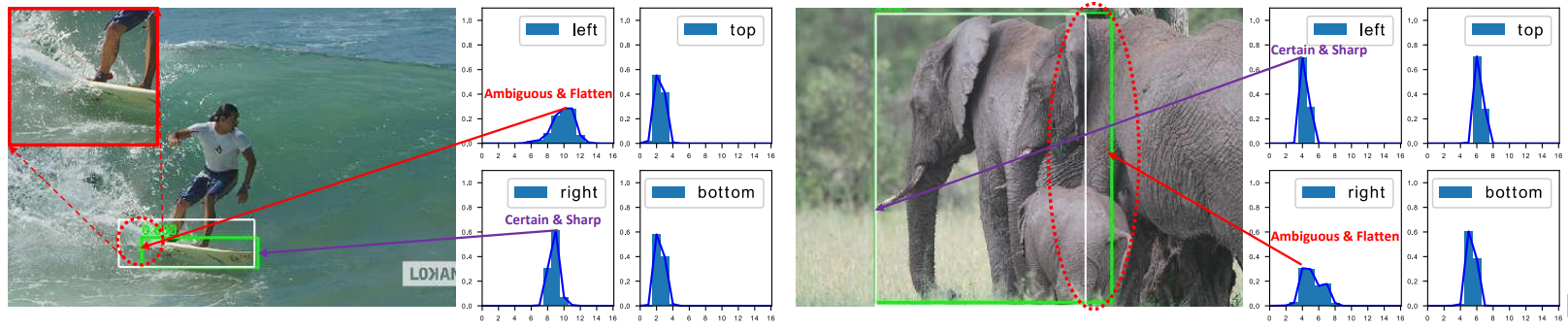
Figure 3: Due to occlusion, shadow, blur, etc., the boundaries of many objects are not clear enough, so that the ground-truth labels (white boxes) are sometimes not credible(可信的) and Dirac delta distribution 仅限于表明这类问题. Instead, the proposed learned representation of General distribution for bounding boxes can reflect the underlying information by its shape, where a flatten distribution denotes the unclear and ambiguous boundaries (see red circles) and a sharp one stands for the clear 情形. The predicted boxes by our model are marked green.

广泛使用的 bounding box representation 可以看作是 the target box coordinates 的 Dirac delta distribution [7,23,8,1,18,26,13,31]。然而，它没有考虑到数据集中的模糊性和不确定性(见 图3 中图像边界不明确)。尽管最近的一些工作[10,4]将 boxes 作为高斯分布进行建模，但这种方法过于简单，无法捕捉 the locations of bounding boxes 的真实分布。实际上，真实的分布可以是更加任意和灵活的[10]，而不需要像高斯函数一样对称。

为解决上述问题，本文为 the bounding boxes and their localization quality 设计了新的表示。

• For localization quality representation，本文建议将其与 the classification score 合并为一个 单一和统一的表示: a classification vector，其中 它的 在 the ground-truth category index 的值 指的是 它的 相应的 localization quality(通常是本文中 the predicted box and the corresponding ground-truth box 之间的 IoU score )。通过这种方式，将 classification score and IoU score 统一为 a joint and single variable (记为 “classificationIoU joint representation”)，可以以 端到端的方式进行训练，同时在推理过程中直接利用(图1(b))。因此，它消除了 训练-测试的不一致性(图1(b))，并使 localization quality and classification 之间具有最强的相关性(图2 (b))。此外，the negatives 将被监督为 0 quality scores，因此整体 quality predictions 变得更加机密和可靠。这对于 dense object detectors 尤其有益，因为它们对整个图像中均匀地(regularly)采样的所有候选对象进行排名。
• For bounding box representation, 本文建议通过 直接学习其连续空间上的离散概率分布来表示 box locations 的任意分布(本文称为"一般分布")，而不引入任何其他更强的先验(如高斯[10,4])。因此，我们可以获得更可靠和准确的 bounding box estimations，同时知道它们的各种潜在分布(见 图3 和补充材料中的 the predicted distributions)。

改进的表示形式对优化提出了挑战。传统上，对于密集检测器，分类分支是用 Focal Loss [18] (FL)优化的。FL 可以通过重塑 the standard cross entropy loss 来成功地处理 class imbalance problem。然而，对于所提出的 classification-IoU joint representation ，除了仍然存在的不平衡风险外，还面临着 continuous IoU label (0∼1) 作为监督的新问题，因为原始 FL 目前只支持离散的 {1,0} 类别标签。通过将 FL 从 {1,0}离散版本 扩展到其连续变体，称为广义 Focal Loss( Generalized Focal Loss (GFL))，成功地解决了这个问题。与 FL 不同的是，GFL 考虑的是一种更一般的情况，即 全局最优解能够指向任意连续值，而不是离散值。

更具体地说，本文中，GFL 可以特化为 Quality Focal Loss (QFL) and Distribution Focal Loss (DFL)，以分别优化改进的两种表示:

• QFL focuses on a sparse set of hard examples and simultaneously produces their continuous 0∼1 quality estimations on the corresponding category;
• DFL 使网络在任意和灵活的分布下，快速专注于学习 target bounding boxes 的 the continuous locations 周围值的概率**。

我们展示了 GFL 的三个优势:

• (1) 当 one-stage detectors 具有 额外的 quality estimation 时，它弥合了训练和测试之间的差距，导致 classification and localization quality 的一个 更简单、联合和有效的表示;
• (2) 很好地建模了 bounding boxes 的灵活潜在分布，提供了更多的信息和准确的 box locations;
• (3) 在不引入额外开销的情况下，单阶段检测器的性能得到持续提升。在COCO test-dev中，GFL在ResNet-101主干上取得了45.0%的AP，超过了最先进的SAPD(43.5%)和ATSS(43.6%)。最好的模型可以实现48.2%的单模型单尺度AP，同时在单个 2080Ti GPU 上以 10 FPS的速度运行。

2. 相关工作

Representation of localization quality. 现有实践如 Fitness NMS [27]， IoU- net [12]， MS R-CNN [11]， FCOS[26]和IoU-aware[29] 利用 单独的分支以 IoU or centerness score 的形式执行 localization quality estimation 。如 第1节 所述，这种单独的表示会导致 训练和测试之间的不一致，以及不可靠的 quality predictions 。PISA[2]和 IoU-balance[28]不增加分支，而是根据 它们 localization qualities 在 classification loss 中赋予不同的权重，增强 the classification score and localization accuracy 之间的相关性。然而，由于权重策略没有改变分类损失目标的最优性，因此其收益是隐式的且有限的。

Representation of bounding boxes. Dirac delta distribution [7,23,8,1,18,26,13,31]支配着过去几年 bounding boxes 的表示。最近，采用高斯假设[10,4]通过引入预测方差来学习不确定性。然而，现有的表示方法要么过于僵化，要么过于简化，无法反映真实数据中复杂的潜在分布。本文进一步放松了假设，直接学习更任意、更灵活的 bounding boxes 一般分布，同时信息量更大、更准确。

3. 方法

在本节中，我们首先回顾了原始的 Focal Loss18，用于学习 one-stage detectors 的 dense classification scores。介绍了改进的 representations of localization quality estimation and bounding boxes 的细节，分别通过提出的 Quality Focal Loss (QFL) and Distribution Focal Loss (DFL) 成功优化。最后，将 QFL 和 DFL 的表述总结为一个统一的视角，称为 广义Focal Loss (GFL),，作为 FL 的灵活扩展，以促进未来的进一步推广和一般性理解。

Focal Loss (FL).

最初的 FL [18]是为了解决单阶段目标检测场景，在训练过程中经常存在 foreground and background classes 之间的极端不平衡。FL的典型形式如下(为简单起见，我们忽略了原始论文[18]中的 \(α_t\)):

\[\left.\mathbf{FL}(p)=-(1-p_t)^\gamma\log(p_t),p_t=\left\{\begin{array}{rl}p,&\text{when}~y=1\\1-p,&\text{when}~y=0\end{array}\right.\right.\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(1) \]

其中，y∈{1,0} 表示 the ground-truth class ，p∈[0,1]表示 标签为 y = 1 的类别的估计概率。γ 是可调的 focusing 参数。具体来说，FL 由标准交叉熵部分 \(−log(p_t)\) 和动态缩放因子部分 \((1−p_t)^γ\) 组成，其中 缩放因子 \((1−p_t)^γ\) 在训练过程中自动降低容易样本的贡献权重，并快速将模型集中在困难样本上。

Quality Focal Loss (QFL).

为了解决上述训练阶段和测试阶段之间的不一致问题，我们提出了 a joint representation of localization quality (i.e., IoU score) and classification score (“classification-IoU” for short), where its supervision softens the standard one-hot category label and leads to a possible float target y ∈ [0, 1] on the corresponding category (see the classification branch in Fig. 4).。其中，y = 0 denotes the negative samples with 0 quality score; 0 < y ≤ 1 stands for the positive samples with target IoU score y。Note that the localization quality label y follows the conventional definition as in [29, 12]: IoU score between the predicted bounding box and its corresponding ground-truth bounding box during training, with a dynamic value being 0∼1. Following [18, 26], we adopt the multiple binary classification with sigmoid operators σ(·) for multi-class implementation. For simplicity, the output of sigmoid is marked as σ.

Since the proposed classification-IoU joint representation requires dense supervisions over an entire image and the class imbalance problem still occurs, the idea of FL must be inherited.However, the current form of FL only supports {1, 0} discrete labels, but our new labels contain decimals(小数). Therefore, we propose to extend the two parts of FL for enabling the successful training under the case of joint representation:

• (1) The cross entropy part \(− log(p_t)\) is expanded into its complete version \(−(1 − y) log(1 − σ) + y log(σ)\)
• (2) The scaling factor part \((1 − p_t)^γ\) is generalized(推广) into the absolute distance between the estimation σ and its continuous label y, i.e., \(|y − σ|^β(β ≥ 0)\), here | · | guarantees the non-negativity. Subsequently, we combine the above two extended parts to formulate the complete loss objective, which is termed as Quality Focal Loss (QFL):

\[\mathbf{QFL}(\sigma)=-|y-\sigma|^\beta\big((1-y)\log(1-\sigma)+y\log(\sigma)\big)\quad\quad\quad\quad\quad\quad\quad(4) \]

Note that σ = y is the global minimum solution of QFL. QFL is visualized for several values of β in Fig. 5(a) under quality label y = 0.5. Similar to FL, the term \(|y-\sigma|^\beta\) of QFL behaves as a modulating(调制的) factor: when the quality estimation of an example is inaccurate(不准确的) and deviated(偏离) away from label y, the modulating factor is relatively large, thus it pays more attention to learning this hard example. As the quality estimation becomes accurate, i.e., σ → y, the factor goes to 0 and the loss for well-estimated examples is down-weighted, in which the parameter β controls the down-weighting rate smoothly (β = 2 works best for QFL in our experiments).

Distribution Focal Loss (DFL)

沿用[26,31]，我们采用 location 到 a bounding box 的 四边 的相对偏移量作为回归目标(见图4中的回归分支)

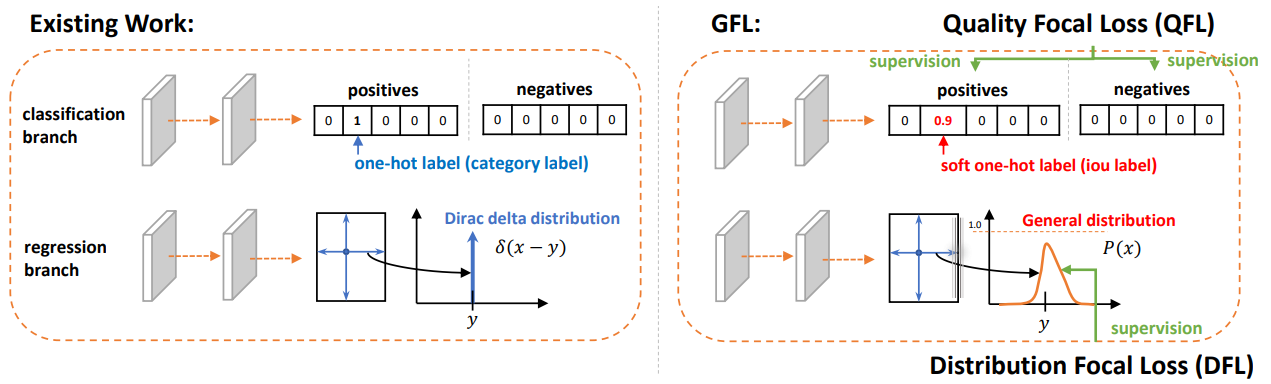
图4：在 dense detectors 的 the head 与传统方法进行比较。GFL 包括 QFL 和 DFL。QFL 有效地学习了a joint representation of classification score and localization quality estimation。DFL 将 the locations of bounding boxes 建模为 General(一般的) 分布，同时迫使网络快速专注于学习 the probabilities of values close to the target coordinates 。

Conventional operations of bounding box regression model the regressed label y as Dirac delta distribution δ(x − y), where it satisfies \(\int_{-\infty}^{+\infty}\delta(x-y)\mathrm{d}x=1\) and is usually implemented through fully connected layers. More formally, the integral(积分) form to recover y is as follows:

\[y=\int_{-\infty}^{+\infty}\delta(x-y)x\mathrm{d}x\quad\quad\quad\quad\quad\quad\quad(3) \]

根据第1节的分析，我们建议不引入任何其他先验, 直接学习 the underlying General distribution \(P(x)\)，而不是 Dirac delta[23, 8, 1, 26, 31]或 Gaussian[4,10]假设。给定标签 y 的最小值为 \(y_0\)，最大值为 \(y_n\) 的范围 (\(y_0≤y≤y_n, n∈N^+\))，我们可以由模型得到 估计值\(\hat{y}\) (\(\hat{y}\) 也满足 \(y_{0}\leq\hat{y}\leq y_{n}\)):

\[\begin{aligned}\hat{y}=\int_{-\infty}^{+\infty}P(x)x\mathrm{d}x=\int_{y_0}^{y_n}P(x)x\mathrm{d}x\end{aligned}\quad\quad\quad\quad\quad\quad\quad(4) \]

为了与卷积神经网络一致，我们 将连续域上的积分转换为离散表示，通过将 范围 \([y_0, y_n]\) 离散为集合 \(\{y_0,y_1,...,y_i,y_{i+1},...,y_{n-1},y_n\}\)，间隔为 偶数∆(为简单起见，我们使用∆= 1)。因此，给定离散分布性质 \(\sum_{i=0}^nP(y_i)=1\)，回归估计值 \(\hat{y}\) 可表示为:

\[\hat{y}=\sum_{i=0}^nP(y_i)y_i\quad\quad\quad\quad\quad\quad\quad(4) \]

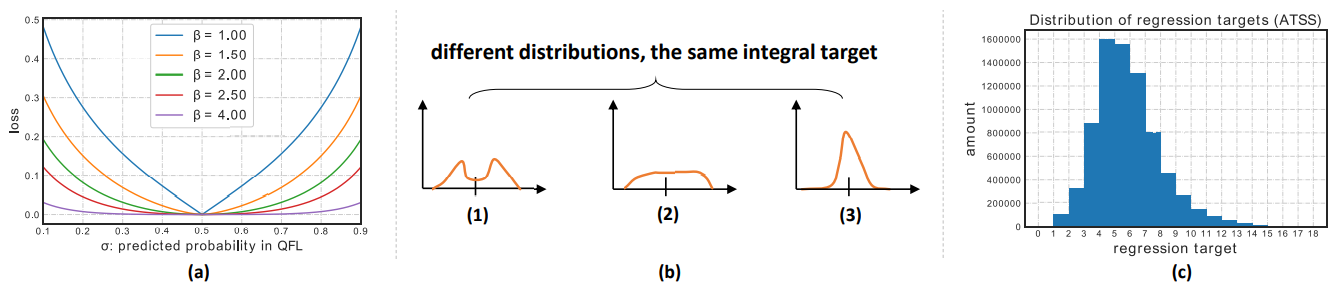
Figure 5: (a): The illustration(说明) of QFL under quality label y = 0.5. (b): Different flexible distributions can obtain the same integral target according to Eq. (4), thus we need to focus on learning probabilities of values around the target for more reasonable and confident predictions (e.g., (3)). (c): The histogram of bounding box regression targets of ATSS over all training samples on COCO trainval35k.

Figure 6: Illustrations of modified versions for separate/implicit and joint representation. The baseline without quality branch is also provided.

因此，\(P(x)\) 可以通过由 n + 1 个单元组成的 softmax S(·) 层轻松实现，为简单起见，P(yi) 记为\(S_i\)。请注意，\(\hat{y}\) 可以使用传统的损失目标(如 SmoothL1 [7]， IoU损失[27]或GIoU损失[24])以端到端的方式进行训练。然而，\(P(x)\) 有无限种取值组合，使得最终的积分结果为 y，如 图5(b) 所示，这可能会降低学习效率。直观上与(1)和(2)相比，分布(3)是紧凑的，并且在边界框估计上更有信心和更精确，这激励我们通过 explicitly encouraging the high probabilities of values that are close to the target y, to optimize the shape of P(x)。此外，通常情况下， the most appropriate underlying location, if exists, would not be far away from the coarse label. 引入 the Distribution Focal Loss (DFL) ，通过显式扩大 \(y_i\) 和 \(y_{i+1}\) 的概率(距离 y 最近的 2 个, \(y_{i}\leq y\leq y_{i+1}\))，迫使网络快速关注标签 y 附近的值。由于 bounding boxes 的学习仅针对正样本，不存在 类不平衡问题的风险，因此我们简单地应用 QFL 中的完全交叉熵部分来定义 DFL:

\[\mathbf{DFL}(\mathcal{S}_i,\mathcal{S}_{i+1})=-\left((y_{i+1}-y)\log(\mathcal{S}_i)+(y-y_i)\log(\mathcal{S}_{i+1})\right)\quad\quad\quad\quad\quad\quad\quad(4) \]

Intuitively(直觉地), DFL aims to focus on enlarging the probabilities of the values around target y (i.e., \(y_i\) 和 \(y_{i+1}\)). The global minimum solution of DFL, i.e, \(\mathcal{S}_i=\frac{y_{i+1}-y}{y_{i+1}-y_i},\mathcal{S}_{i+1}=\frac{y-y_i}{y_{i+1}-y_i}\) (see Supplementary Materials), can guarantee the estimated regression target \(\hat{y}\) infinitely(无限地) close to the corresponding label y, i.e., \(\begin{aligned}\hat{y}=\sum_{j=0}^nP(y_j)y_j=\mathcal{S}_iy_i+\mathcal{S}_{i+1}y_{i+1}=\frac{y_{i+1}-y}{y_{i+1}-y_i}y_i+\frac{y-y_i}{y_{i+1}-y_i}y_{i+1}=y\end{aligned}\), which also ensures its correctness as a loss function.

参考：

大白话 Generalized Focal Loss https://zhuanlan.zhihu.com/p/147691786

一文了解目标检测边界框概率分布 https://zhuanlan.zhihu.com/p/151398233

深入理解一下Generalized Focal Loss v1 & v2 https://zhuanlan.zhihu.com/p/357415257

https://www.zhihu.com/people/ai-ai-zi-qiao