机器学习分类模型评价指标之混淆矩阵
对于每一个做模型的人而言，如何评价一个模型的有多“好”是一件非常重要的事情。
In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as an error matrix,[10] is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one (in unsupervised learning it is usually called a matching matrix). Each row of the matrix represents the instances in an actual class while each column represents the instances in a predicted class, or vice versa – both variants are found in the literature.[11] The name stems from the fact that it makes it easy to see whether the system is confusing two classes (i.e. commonly mislabeling one as another).
在机器学习领域，特别是在统计分类的问题中，混淆矩阵，也被称为 错误矩阵，是一种独特的表排列，可以可视化一个算法的性能，通常是监督学习(在非监督学习中，它通常被称为 匹配矩阵)。矩阵的每一行代表一个实际类中的实例，而每一列代表一个预测类中的实例，反之亦然-这两种变体都可以在文献[11]中找到。这个名字源于这样一个事实，即它很容易看出系统是否混淆了两个类(即通常将一个类错误标记为另一个类)。
看来行是真实或者预测都是可以的。
It is a special kind of contingency table, with two dimensions ("actual" and "predicted"), and identical sets of "classes" in both dimensions (each combination of dimension and class is a variable in the contingency table).
它是一种特殊类型的关联表，具有两个维度(“实际的”和“预测的”)，在两个维度中都有相同的“类”集合(维度和类的每个组合都是关联表中的一个变量)。
Example
Given a sample of 12 individuals, 8 that have been diagnosed with cancer and 4 that are cancer-free, where individuals with cancer belong to class 1 (positive) and non-cancer individuals belong to class 0 (negative), we can display that data as follows:
例子
假设有 12 个人，其中 8人 被诊断为癌症，4人 没有癌症，其中癌症患者属于 class 1 (positive) ，非癌症患者属于 class 0 (negative)，我们可以将数据显示为:
Assume that we have a classifier that distinguishes between individuals with and without cancer in some way, we can take the 12 individuals and run them through the classifier. The classifier then makes 9 accurate predictions and misses 3: 2 individuals with cancer wrongly predicted as being cancer-free (sample 1 and 2), and 1 person without cancer that is wrongly predicted to have cancer (sample 9).
假设我们有一个分类器，可以在某种程度上区分癌症患者和非癌症患者，我们可以将这 12个 个体通过分类器进行分类。分类器做出了 9个准确的预测，但 有3个漏检: 2个癌症患者 被错误地预测为无癌症(样本1 和 2)，1个没有癌症的人被错误地预测为癌症(样本9)。
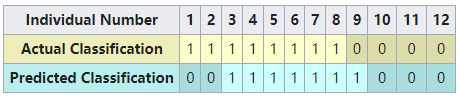
Notice, that if we compare the actual classification set to the predicted classification set, there are 4 different outcomes that could result in any particular column. One, if the actual classification is positive and the predicted classification is positive (1,1), this is called a true positive result because the positive sample was correctly identified by the classifier. Two, if the actual classification is positive and the predicted classification is negative (1,0), this is called a false negative result because the positive sample is incorrectly identified by the classifier as being negative. Third, if the actual classification is negative and the predicted classification is positive (0,1), this is called a false positive result because the negative sample is incorrectly identified by the classifier as being positive. Fourth, if the actual classification is negative and the predicted classification is negative (0,0), this is called a true negative result because the negative sample gets correctly identified by the classifier.
注意，如果我们将实际的分类集合与预测的分类集合进行比较，在任何特定的列上都可能有4种不同的结果。
- 第一，如果实际分类结果为 positive，且预测分类结果为 positive (1,1)，则称为 true positive 结果，因为分类器正确地识别了 positive 样本。
- 第二，如果实际分类是 positive ，而预测分类是 negative (1,0)，这被称为 false negative 结果，因为分类器错误地将 positive 样本识别为 negative 样本。
- 第三，如果实际分类结果为 negative，而预测分类结果为 positive (0,1)，则称为 false positive 结果，因为分类器错误地将 negative 样本识别为 positive 样本。
- 第四，如果实际分类结果为 negative ，而预测分类结果为 negative (0,0)，则称为 true negative 结果，因为分类器正确地识别了 negative 样本。
We can then perform the comparison between actual and predicted classifications and add this information to the table, making correct results appear in green so they are more easily identifiable.
然后，我们可以在实际分类和预测分类之间进行比较，并将这些信息添加到表中，使正确的结果以绿色显示，以便更容易识别。
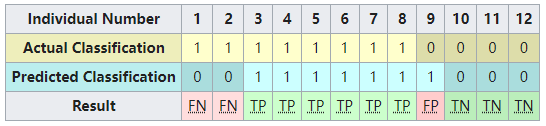
The template for any binary confusion matrix uses the four kinds of results discussed above (true positives, false negatives, false positives, and true negatives) along with the positive and negative classifications. The four outcomes can be formulated in a 2×2 confusion matrix, as follows:
任何 binary 混淆矩阵 的模板都使用上述四种结果(true positives, false negatives, false positives, and true negatives)以及 positive and negative 分类。这四种结果可以用 2×2混淆矩阵 表示，如下所示:
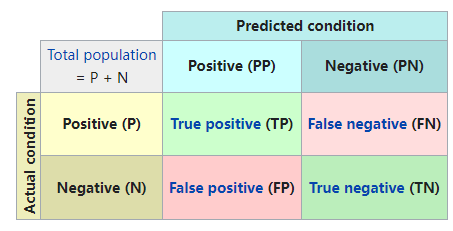
The color convention of the three data tables above were picked to match this confusion matrix, in order to easily differentiate the data.
Now, we can simply total up each type of result, substitute into the template, and create a confusion matrix that will concisely summarize the results of testing the classifier:
选择上面前三个数据表的颜色约定来匹配这个混淆矩阵，以便于区分数据。
现在，我们可以简单地将每种类型的结果相加，代入这个模板，并创建一个混淆矩阵，它将简要地总结分类器测试的结果:
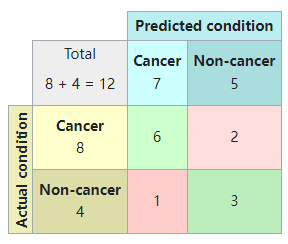
In this confusion matrix, of the 8 samples with cancer, the system judged that 2 were cancer-free, and of the 4 samples without cancer, it predicted that 1 did have cancer. All correct predictions are located in the diagonal of the table (highlighted in green), so it is easy to visually inspect the table for prediction errors, as values outside the diagonal will represent them. By summing up the 2 rows of the confusion matrix, one can also deduce the total number of positive (P) and negative (N) samples in the original dataset, i.e. \({\displaystyle P=TP+FN}\) \({\displaystyle P=TP+FN}\) and \({\displaystyle N=FP+TN}\)\({\displaystyle N=FP+TN}\).
在这个混淆矩阵中，8个患癌症的样本中，系统判断2个为无癌症样本，4个未患癌症的样本中，系统预测1个确实患癌症。所有正确的预测都位于表的对角线上(以绿色高亮显示)，因此很容易从视觉上检查表中的预测误差，因为对角线以外的值表示它们。通过将混淆矩阵的两行相加，还可以推断出原始数据集中 positive (P) 样本 和 negative (N) 样本的总数，即 \({\displaystyle P=TP+FN}\) and \({\displaystyle N=FP+TN}\)。
Table of confusion
In predictive analytics, a table of confusion (sometimes also called a confusion matrix) is a table with two rows and two columns that reports the number of true positives, false negatives, false positives, and true negatives. This allows more detailed analysis than simply observing the proportion of correct classifications (accuracy). Accuracy will yield misleading results if the data set is unbalanced; that is, when the numbers of observations in different classes vary greatly.
For example, if there were 95 cancer samples and only 5 non-cancer samples in the data, a particular classifier might classify all the observations as having cancer. The overall accuracy would be 95%, but in more detail the classifier would have a 100% recognition rate (sensitivity) for the cancer class but a 0% recognition rate for the non-cancer class. F1 score is even more unreliable in such cases, and here would yield over 97.4%, whereas informedness removes such bias and yields 0 as the probability of an informed decision for any form of guessing (here always guessing cancer).
According to Davide Chicco and Giuseppe Jurman, the most informative metric to evaluate a confusion matrix is the Matthews correlation coefficient (MCC).[20]
Other metrics can be included in a confusion matrix, each of them having their significance and use.
混淆表
在预测分析中，混淆表(有时也称为混淆矩阵)是一个两行两列的表，其中记录了 true positives, false negatives, false positives, and true negatives 的数量。这比简单地观察正确分类的比例(accuracy)可以进行更详细的分析。如果数据集不平衡，Accuracy 会产生误导性的结果; 也就是说，当不同类别的观测值数量差异很大时。
例如，如果数据中有95个癌症样本，而只有5个非癌症样本，特定的分类器可能会将所有观测值分类为癌症。总体 accuracy 为 95%，但更详细地说，分类器对 癌症类别 的识别率(sensitivity)为100%，而对 非癌症类别的识别率 为 0%。在这种情况下，F1得分甚至更加不可靠，这里的得分将超过 97.4% ，而 informedness 消除了这种 bias，并且对于任何形式的猜测(这里总是猜测癌症)产生 informed decision 的概率为 0。
Davide Chicco和Giuseppe Jurman认为，评估混淆矩阵最具信息量的指标是马修斯相关系数(Matthews correlation coefficient (MCC))。
其他指标可以包含在混淆矩阵中，每个指标都有自己的重要性和用途。
Confusion matrices with more than two categories
Confusion matrix is not limited to binary classification and can be used in multi-class classifiers as well.[30] The confusion matrices discussed above have only two conditions: positive and negative. For example, the table below summarizes communication of a whistled language between two speakers, zero values omitted for clarity.[31]
超过两类的混淆矩阵
混淆矩阵不局限于二分类，也可以用于多分类器。 上面讨论的混淆矩阵只有两个条件:positive and negative。 例如，下表总结了两个说话者之间口哨语言的交流，为清晰起见省略了0值.
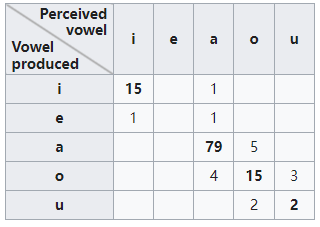
对于多分类问题，或者在二分类问题中，我们有时候会有多组混淆矩阵，例如：多次训练或者在多个数据集上训练的结果，那么估算全局性能的方法有3种，分为宏平均（macro-average）、微平均（micro-average）和加权平均（Weighted-Average）。
- 简单理解，宏平均就是先算出每个混淆矩阵的P值和R值，然后取得平均 P 值 macro-P 和平均 R 值 macro-R，再算出Fβ或F1。
- 微平均则是计算出混淆矩阵的平均TP、FP、TN、FN，接着进行计算P、R，进而求出 Fβ 或 F1。其它分类指标同理，均可以通过宏平均/微平均计算得出。
- 从计算的角度讲，先对每个类求值，再取平均得到 Macro Average 会比较容易．但是当数据集中存在严重类别不平衡的问题时，就不适宜单纯使用 Macro Average．此时可以采取weighted average. 具体来说当我们计算 Macro Average 时候我们给每个类赋予相同的权重，但是当样本不平衡时，不适宜给每个类赋予同样的权重，我们可以根据每个类的样本量，给每个类赋予不同的权重，这就是 weighted average 的计算方法。
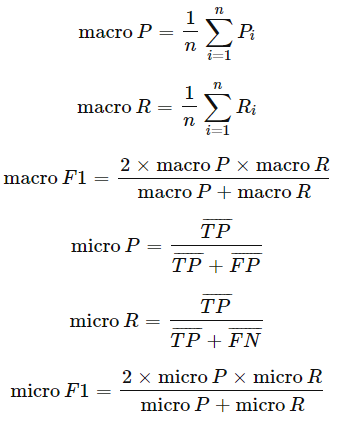
在多分类任务场景中，如果非要用一个综合考量的 metric 的话，宏平均会比微平均更好一些，因为宏平均受稀有类别影响更大。宏平均平等对待每一个类别，所以它的值主要受到稀有类别的影响，而微平均平等考虑数据集中的每一个样本，所以它的值受到常见类别的影响比较大。
显然，目标检测中的 mAP 的计算就是 宏平均 的做法。
个人理解
T: True。表示该模型预测正确。假设场景为预测明天是否下雨？无非两种情况：
- 情况1：
- 明天实际上真的 下雨了，模型也预测为 下雨，模型预测正确。所以为 T。
- 情况2：
- 明天 没有下雨，模型预测也是不下雨，模型预测正确。也是 T。
F: False。表示该模型预测错误。也无非两种情况：
- 情况3：
- 明天真的下雨了，模型也预测为 不下雨，模型预测错误。所以为 F。
- 情况4：
- 明天没有下雨，模型预测是 下雨，模型预测错误。F。
P：Positive。N: Negative。 只和模型预测的结果有关系。
假设 下雨为 正(Positive--P)，不下雨为 负(Negative--N)。所以上面的情况如下：
- 情况1： T P
- 情况2： T N
- 情况3： F N
- 情况4： F P
当然，也可以假设 不下雨为 正(Positive--P)，下雨为 负(Negative--N)。所以上面的情况如下：
- 情况1： T N
- 情况2： T P
- 情况3： F P
- 情况4： F N
混淆矩阵每个位置要填的数字就是 这四种情况的样本个数。
混淆矩阵实际用途
1、能够帮助我们迅速可视化各种类别误分为其它类别的比重，这样能够帮我们调整后续模型，比如一些类别设置权重衰减。
2、在一些论文的实验分析中，可以列出混淆矩阵，行和列均为 label 种类，可以通过该矩阵验证自己 model 预测复杂 label 的能力强于其他model，只要自己 model 复杂 label 误判为其它类别比其他 model 误判的少，就可以说明自己 model 预测复杂 label 的能力强于其他 model。
