csp-s模拟4
A. 商品
可以发现,选取的 \(l,r\) 一定有一个边界是原序列的数,所以我们 \(O(n)\) 枚举 \(l/r\) ,考虑如何快速的求出临项差的
绝对值,我们可以把相邻两个数大的放到一个数组,小的放到一个数组,先排序,每次枚举的 \(l,r\) 二分查找在数组中的
位置,贡献就是 \(l\) 左边的数个数 * \(l\)+\(r\) 右边的数个数 * \(r\)+ \(l,r\) 中间的数的和,前两项 \(O(1)\) 算,后一项前缀和优化一下
总复杂度 \(O(nlogn)\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
const int maxn=2e5+10;
using namespace std;
int a[maxn],q[maxn],d,top,n,da[maxn],xi[maxn],ans,sum1[maxn],sum2[maxn],s,t;
signed main()
{
freopen("goods.in","r",stdin);
freopen("goods.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>d;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=2;i<=n;i++)
{
da[i-1]=max(a[i-1],a[i]);
xi[i-1]=min(a[i-1],a[i]);
}
sort(da+1,da+n);sort(xi+1,xi+n);
for(int i=1;i<=n;i++)
{
if(a[i]!=a[i-1])q[++top]=a[i];
}
n--;
for(int i=1;i<=n;i++)
{
sum1[i]=sum1[i-1]+da[i];
sum2[i]=sum2[i-1]+xi[i];
}
for(int i=1;i<=top;i++)
{
int l=q[i],r=l+d,minn=0,maxx=0;
s=lower_bound(da+1,da+1+n,l)-da;
t=lower_bound(da+1,da+1+n,r+1)-da;
maxx=(s-1)*l+sum1[t-1]-sum1[s-1]+(n-t+1)*r;
s=lower_bound(xi+1,xi+1+n,l)-xi;
t=lower_bound(xi+1,xi+1+n,r+1)-xi;
minn=(s-1)*l+sum2[t-1]-sum2[s-1]+(n-t+1)*r;
ans=max(ans,maxx-minn);
}
for(int i=1;i<=top;i++)
{
int r=q[i],l=r-d,minn=0,maxx=0;
s=lower_bound(da+1,da+1+n,l)-da;
t=lower_bound(da+1,da+1+n,r+1)-da;
maxx=(s-1)*l+sum1[t-1]-sum1[s-1]+(n-t+1)*r;
s=lower_bound(xi+1,xi+1+n,l)-xi;
t=lower_bound(xi+1,xi+1+n,r+1)-xi;
minn=(s-1)*l+sum2[t-1]-sum2[s-1]+(n-t+1)*r;
ans=max(ans,maxx-minn);
}
cout<<ans<<'\n';
return 0;
}
/*
8 3
3 1 4 1 5 9 2 6
*/
B. 价值
感谢5k和wps在这道题对我的贡献
考虑树形 \(dp\) ,\(f_{u,i,j,k}\) 表示 \(u\) 的子树中,\(u\) 是否匹配,最左的叶子节点是否匹配,最右的叶子节点是否匹配。
\(dp\) 时就一个个合并子树,用合并前的整个树加上这个子树去更新合并后的整个树,分讨很多,看代码吧。
边界:\(f_{u,0,0,0}=1\),如果 \(u\) 是叶子节点,则 \(f_{u,1,0,1}=f_{u,1,1,0}=1\)(就是叶子节点向右/左匹配时自己也同时匹配)
点击查看代码
#include<bits/stdc++.h>
#define int long long
const int mod=998244353;
const int maxn=2e5+10;
using namespace std;
int head[maxn],to[maxn],nxt[maxn],tot,ans;
int n,f[maxn][2][2][2];
void add(int x,int y)
{
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int mo(int x)
{
// cout<<x<<endl;
return x>=mod?x%mod:x;
}
void lsx(int x)
{
f[x][0][0][0]=1;
int a[2][2][2];
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
lsx(y);
if(i==head[x])
{
f[x][1][1][1]=f[y][0][1][1];
f[x][1][0][0]=f[y][0][0][0];
f[x][1][1][0]=f[y][0][1][0];
f[x][1][0][1]=f[y][0][0][1];
f[x][0][1][1]=mo(f[y][0][1][1]+f[y][1][1][1]);
f[x][0][1][0]=mo(f[y][0][1][0]+f[y][1][1][0]);
f[x][0][0][1]=mo(f[y][0][0][1]+f[y][1][0][1]);
f[x][0][0][0]=mo(f[y][0][0][0]+f[y][1][0][0]);
}
else
{
for(int j=0;j<=1;j++)for(int k=0;k<=1;k++)for(int s=0;s<=1;s++) a[j][k][s]=f[x][j][k][s];
f[x][1][1][1]=mo(mo(a[1][1][1]*mo(f[y][1][1][1]+f[y][0][1][1]))+mo(a[0][1][1]*f[y][0][1][1]))+mo(mo(a[1][1][0]*mo(f[y][1][0][1]+f[y][0][0][1]))+mo(a[0][1][0]*f[y][0][0][1]));
f[x][1][1][0]=mo(mo(a[1][1][1]*mo(f[y][1][1][0]+f[y][0][1][0]))+mo(a[0][1][1]*f[y][0][1][0]))+mo(mo(a[1][1][0]*mo(f[y][1][0][0]+f[y][0][0][0]))+mo(a[0][1][0]*f[y][0][0][0]));
f[x][1][0][1]=mo(mo(a[1][0][1]*mo(f[y][1][1][1]+f[y][0][1][1]))+mo(a[0][0][1]*f[y][0][1][1]))+mo(mo(a[1][0][0]*mo(f[y][1][0][1]+f[y][0][0][1]))+mo(a[0][0][0]*f[y][0][0][1]));
f[x][1][0][0]=mo(mo(a[1][0][1]*mo(f[y][1][1][0]+f[y][0][1][0]))+mo(a[0][0][1]*f[y][0][1][0]))+mo(mo(a[1][0][0]*mo(f[y][1][0][0]+f[y][0][0][0]))+mo(a[0][0][0]*f[y][0][0][0]));
f[x][0][1][1]=mo(mo(a[0][1][1]*mo(f[y][0][1][1]+f[y][1][1][1]))+mo(a[0][1][0]*mo(f[y][0][0][1]+f[y][1][0][1])));
f[x][0][1][0]=mo(mo(a[0][1][1]*mo(f[y][0][1][0]+f[y][1][1][0]))+mo(a[0][1][0]*mo(f[y][0][0][0]+f[y][1][0][0])));
f[x][0][0][1]=mo(mo(a[0][0][1]*mo(f[y][0][1][1]+f[y][1][1][1]))+mo(a[0][0][0]*mo(f[y][0][0][1]+f[y][1][0][1])));
f[x][0][0][0]=mo(mo(a[0][0][1]*mo(f[y][0][1][0]+f[y][1][1][0]))+mo(a[0][0][0]*mo(f[y][0][0][0]+f[y][1][0][0])));
}
}
if(!head[x]) f[x][1][1][0]=f[x][1][0][1]=1;
}
signed main()
{
freopen("value.in","r",stdin);
freopen("value.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n;
for(int i=2;i<=n;i++)
{
int x;
cin>>x;
add(x,i);
}
lsx(1);
ans=mo(mo(f[1][1][0][0]+f[1][1][1][1])+mo(f[1][0][0][0]+f[1][0][1][1]));
cout<<ans;
return 0;
}
/*
18
1 2 3 4 5 6 4 3 2 2 11 2 13 2 2 1 1
*/
C. 货币
不枉我寒假学了整7天的网络流,经5k一点就会了,也是下午来了很快就 \(A\) 了
考虑横着一张 \(2*n\) 的图,上下两条 \((1,i)->(1,i+1),(2,i)->(2,i+1)\) 显然这两条边只能同时走一条
没限制时直接裸的最小割就行了,考虑加上限制应该如何割边
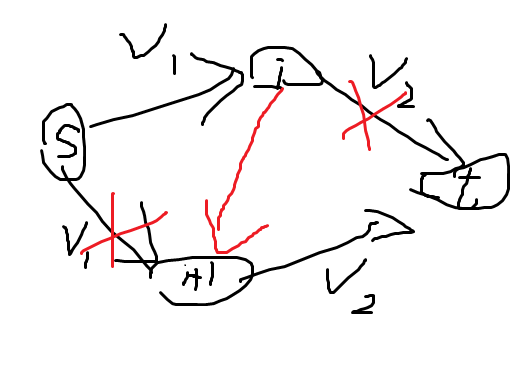
\(v1,v2\) 分别表示\((1,i)->(1,i+1),(2,i)->(2,i+1)\) 的边权,我们想让割这两个红叉的边时,多付出代价,只需要
像上图一样,连一条边,使得图又联通导致必须多割一条边或换别的边割,
\((1,i)->(2,i)/(2,i)->(1,i)\) 的这种连接两条路的边可以发现和限制边是等价的,按上面方法连即可
对于第一条和最后一条链接上下两条路的边,可以直接把第一条边边权加到第二条路的第一条横向边,把最后一条边边权加到
第一条路的最后一条横向边即可,没必要新建两个竖边
点击查看代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e7+5;
const int INF=0x7f7f7f7f;
int n,s,t,p,h,r,cnt,now,w,sum,d[maxn>>4],b[maxn>>4],c[maxn>>4];
int head[maxn<<1],tot=1;
struct node
{
int to,nxt,flow,dis;
}m[maxn<<1];
void add(int x,int y,int z)
{
m[++tot].to=y;
m[tot].nxt=head[x];
m[tot].dis=z;
head[x]=tot;
m[tot].flow=0;
}
void addm(int x,int y,int z)
{
add(x,y,z);add(y,x,0);
}
int deep[maxn],a[maxn];
queue<int>q;
bool bfs()
{
for(int i=1;i<=t;i++)deep[i]=0;
deep[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
a[u]=head[u];
for(int i=head[u];i;i=m[i].nxt)
{
if(!deep[m[i].to]&&m[i].dis>m[i].flow)
{
deep[m[i].to]=deep[u]+1;
q.push(m[i].to);
}
}
}
return deep[t];
}
int dfs(int now,int fa1)
{
if(now==t||!fa1)return fa1;
int fa=0,d;
for(int i=a[now];i;i=m[i].nxt)
{
a[now]=i;
if(deep[m[i].to]==deep[now]+1&&(d=dfs(m[i].to,min(fa1-fa,m[i].dis-m[i].flow))))
{
m[i].flow+=d;
m[i^1].flow-=d;
fa+=d;
if(fa==fa1) break;
}
}
return fa;
}
void dinic()
{
int res=0;
while(bfs())
{
res+=dfs(0,INF);
}
cout<<res<<'\n';
}
signed main()
{
freopen("currency.in","r",stdin);
freopen("currency.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>p;
s=0,t=n+1;
for(int i=1;i<n;i++)
cin>>d[i];
for(int i=1;i<=n;i++)
cin>>b[i];
for(int i=1;i<n;i++)
cin>>c[i];
c[1]+=b[1];d[n-1]+=b[n];
for(int i=1;i<n;i++)
addm(s,i,d[i]);
for(int i=2;i<n;i++)
addm(i,i-1,b[i]),addm(i-1,i,b[i]);
for(int i=1;i<n;i++)
addm(i,t,c[i]);
for(int i=1;i<=p;i++)
{
int x,y,z;
cin>>x>>y>>z;
addm(y,x,z);
}
dinic();
return 0;
}

