难存的情缘
抽象的题目(咱就是说,这个”难存的情缘“是指要把矿掏空吗)
题目
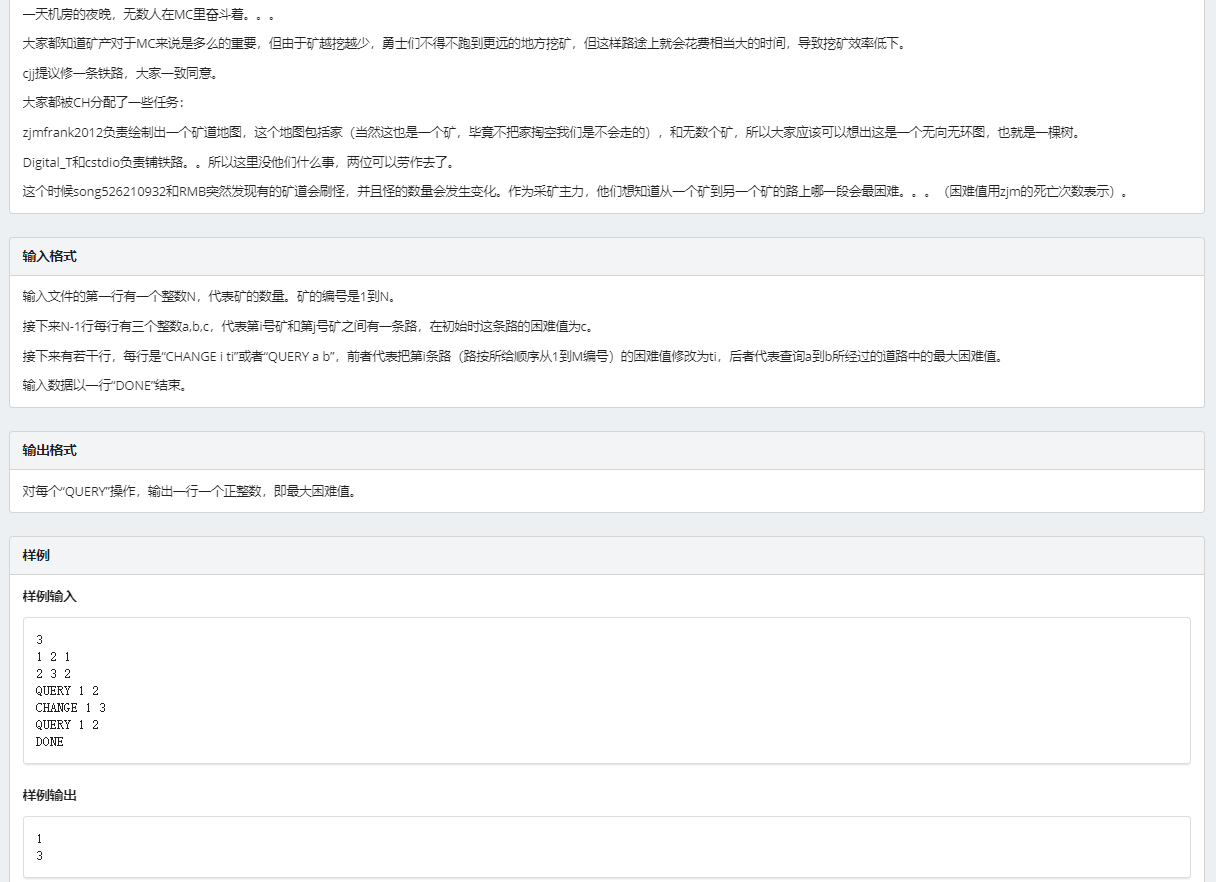
分析
这个题目还是比较好理解的,我们需要干的有 \(2\) 个操作,但实际上有 \(3\) 个
- 1 :边权转点权
- 2 :单点修改
- 3 :链上最大值查询
很明显是树刨板子题,操作中需要注意的有三点,如何转边权,最大值点权查多了,修改时的边与点的对应
点券转边权
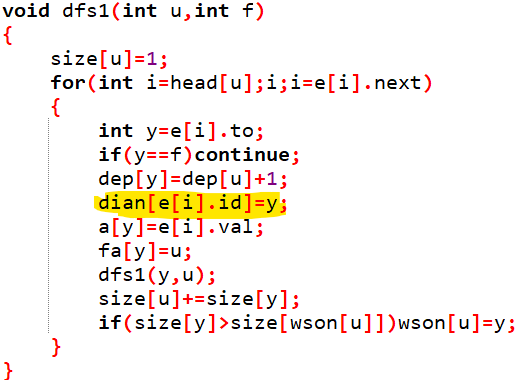
还是很好处理的,在 \(dfs\) 预处理时将边权存一下即可,就是荧光笔标注的这行
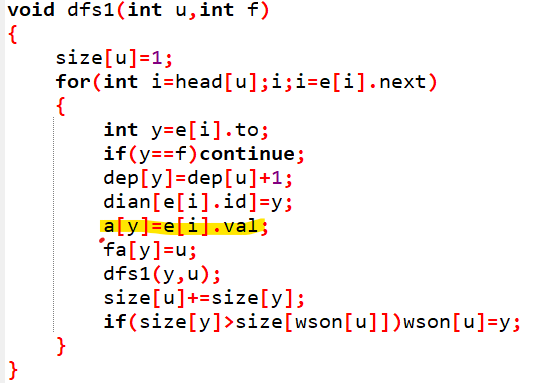
最大值查询
根据上面的代码,我们发现,边权存在边上深度较大的那个点上,这就会导致一个问题,如图
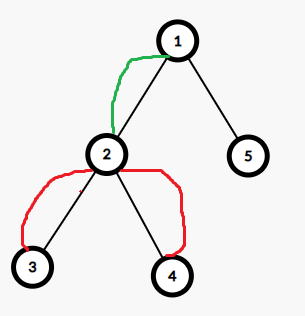
假设我们求 \(3-4\) 这条路上的最大值,那实际上我们在树上找的是 \(3-2-4\) 这条路上的点权最大值,很显然,我们要找
红色的边,但操作上却多了一条绿色的边。。。真鸡肋啊.
那我们如何解决呢,我们简单推广一下可以发现,实际上多的边就是求得两点的 \(lca\) 的值,也就是链上深度最小的点
这样就很显然了,只要在求解时,在指针跳到同一条重链以后,求深度小的点加一到深度大的点的值即可
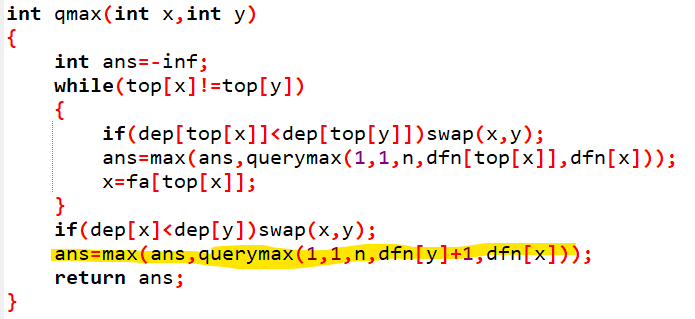
还是荧光笔标的这一行。。。
对应
这个问题还是困扰了我七七 \(=10\) 分钟的,当时一直在想 \(1e5\) 的边,那求边和边的关系那不得开个 \(1e10\) 的数组吗
这不炸我***,所以 \(pass\) 了啊,然后就突然想到了(我觉得是发呆后的灵光乍现),直接在链表存储的时候多开一个
\(id\),这个数组存的实际上就是这个边的编号,还是在 \(dfs\) 预处理时,新开一个对应数组 \(dian\),下标是边号,存的是点
号,对应一下就行了,依旧是荧光笔标注的这行
solution
点击查看代码
#include<bits/stdc++.h>
#define lid id<<1
#define rid id<<1|1
const int maxn=1e5+10;
const int inf=0x7f7f7f7f;
using namespace std;
int n,t,a[maxn<<2];
struct node{int to,next,val,id;}e[maxn<<2];
struct tree{int maxx;}m[maxn<<4];
int tot,head[maxn];
int size[maxn],wson[maxn],fa[maxn],dep[maxn],top[maxn],dian[maxn];
int dfn[maxn],pre[maxn],cnt=0;
void add(int x,int y,int z,int i)
{
e[++tot].to=y;
e[tot].val=z;
e[tot].id=i;
e[tot].next=head[x];
head[x]=tot;
}
void addm(int x,int y,int z,int i)
{
add(x,y,z,i),add(y,x,z,i);
}
void dfs1(int u,int f)
{
size[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int y=e[i].to;
if(y==f)continue;
dep[y]=dep[u]+1;
dian[e[i].id]=y;
a[y]=e[i].val;
fa[y]=u;
dfs1(y,u);
size[u]+=size[y];
if(size[y]>size[wson[u]])wson[u]=y;
}
}
void dfs2(int u,int topfa)
{
dfn[u]=++cnt;
pre[cnt]=u;
top[u]=topfa;
if(wson[u])dfs2(wson[u],topfa);
for(int i=head[u];i;i=e[i].next)
{
int y=e[i].to;
if(y==fa[u]||y==wson[u])continue;
dfs2(y,y);
}
}
void up(int id)
{
m[id].maxx=max(m[lid].maxx,m[rid].maxx);
}
void build(int id,int l,int r)
{
int mid=(l+r)>>1;
if(l==r)
{
m[id].maxx=a[pre[l]];
return ;
}
build(lid,l,mid);
build(rid,mid+1,r);
up(id);
}
void update(int id,int l,int r,int x,int y)
{
if(l==r)
{
m[id].maxx=y;
return ;
}
int mid=(l+r)>>1;
if(x<=mid)update(lid,l,mid,x,y);
else update(rid,mid+1,r,x,y);
up(id);
}
int querymax(int id,int l,int r,int x,int y)
{
int mid=(l+r)>>1,ans=-inf;
if(x<=l&&r<=y)return m[id].maxx;
if(x<=mid)ans=max(ans,querymax(lid,l,mid,x,y));
if(y>mid)ans=max(ans,querymax(rid,mid+1,r,x,y));
up(id);
return ans;
}
int qmax(int x,int y)
{
int ans=-inf;
while(top[x]!=top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
ans=max(ans,querymax(1,1,n,dfn[top[x]],dfn[x]));
x=fa[top[x]];
}
if(dep[x]<dep[y])swap(x,y);
ans=max(ans,querymax(1,1,n,dfn[y]+1,dfn[x]));
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<n;i++)
{
int x,y,z;
scanf("%d%d%d",&x,&y,&z);
addm(x,y,z,i);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
char ss[10];
while(1)
{
int x,y;
scanf("%s",ss+1);
if(ss[1]=='D')break;
scanf("%d%d",&x,&y);
if(ss[1]=='Q')
{
printf("%d\n",qmax(x,y));
}
else
{
// cout<<endl<<dian[x]<<endl;
update(1,1,n,dfn[dian[x]],y);
}
}
return 0;
}

