网络流总结
琐记
这玩意是之前寒假集训时学二分图时被忽悠去学的，今天又回去复习了一下，想写篇总结。
其他的后面有时间再来填坑，先咕着。。。
最大流最小割定理
内容：任何一个网络的最大流量等于最小割中的边容量之和
这玩意看蓝书解释没咋懂，我自己感性理解了一下，有不对的各位指点一下啊
一定注意，网络流的图是有向无环图
假设我们现在有如下的网络，
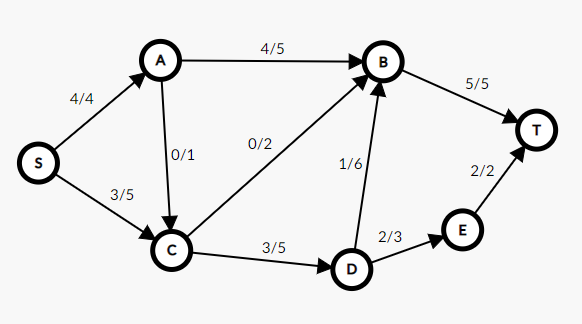
网络中的边我们可分为三类：
- 1：满流边
- 2：被满流边影响的边（不满流但有流量）
- 3：不含流量的边（即不被影响的边）
其最大流为7，我们要寻找一些边让他割去使得S与T不连通，很显然我们要在上面一条路S-A-B-T和下面一条路S-C-D-E-T中
都至少选择一条路将其割掉，而我们要使割去的流量最小，那一定是去割有流量的边（不然你割他干啥），而这些有流量的边中
一定存在至少一条满流的情况才能构成最大流，而这满流的边可能是由之前多条边的流量之和，显然，这之前多条边的流量之和
一定大于等于流量之和，为使S和T不连通，这条路上我们要么割去这条满流的边，要么把其前面的边全割去才能保证这条路不
通，如果只割之前边一部分的话，那另一部分肯定可以与满流的边相连达到连通的目的，所以对于这条路，他的最大流即为
其最小割，而整张网络的流量是由很多这样的满流边和其影响的边组成，均符合上述情况。而那些没有流量的边为什么不用
被考虑呢，首先这些边肯定不与T相连，不然他肯定可以是满流边或被其影响的边之一，其次这些边上没有流量是因为这些边
位置右边的边肯定有满流的了，且其前面没有小于后面那边流量的满流的边（不然不是最大流），那我们割的话肯定是割右边
那个满流的边更优，所以我们直接就将后面的满流边割去即可，这种边割去后即保证了最优也保证了没流的边与后面的T断了
如果后面的边不满流，前面的边满流了，同样割去满流的边更优，这样就是让其与前面的S断了，这种边实际上就是那些被潜
在影响的边，就像图中的C-B一样，它的流量是被别的边给“抢了”，这也是为什么不会出现割去边后原来没有流量的边使S与T
联通的原因。
综上，割满流边，让被满流边影响的边和没流量的边与S或T中的一个不连通，出来的值即为最小割，同为最大流
Dinic算法
残量网络
定义：网络中所有节点及剩余流量大于0的边组成的图
层次
定义：从原点到一个点至少需要经过几条边即为这个点的层次
分层图
定义：在残量网络中根据每个点的层次将点划为不同的点集，其组成的这个子图即为分层图
\(Dinic\)算法就是不断在网络中构造分层图，然后\(dfs\)更新流量，直到残量网路不能联通 \(S\) 与 \(T\) ，复杂度上界 \(n^{2}m\)
板子
int deep[MAXN],a[MAXN];
queue<int>q;
bool bfs()
{
for(int i=1;i<=t;i++)deep[i]=0;
deep[s]=1;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
a[u]=head[u];
for(int i=head[u];i;i=m[i].nxt)
{
if(!deep[m[i].to]&&m[i].dis>m[i].flow)
{
deep[m[i].to]=deep[u]+1;
q.push(m[i].to);
}
}
}
return deep[t];
}
int dfs(int now,int fa1)
{
if(now==t||!fa1)return fa1;
int fa=0,d;
for(int i=a[now];i;i=m[i].nxt)
{
a[now]=i;
if(deep[m[i].to]==deep[now]+1&&(d=dfs(m[i].to,min(fa1-fa,m[i].dis-m[i].flow))))
{
m[i].flow+=d;
m[i^1].flow-=d;
fa+=d;
if(fa==fa1) break;
}
}
return fa;
}
void dinic()
{
int res=0;
while(bfs())
{
res+=dfs(0,INF);
}
printf("%d\n",res);
}
