A Primer on Boolean Satisfiability 布尔满足性入门介绍
SAT问题： 给定一个布尔表达式，看是否有一组赋值使得表达式为true.
SAT属于典型的NP完全问题，决定SAT的最坏情况是2的n次方，尝试n个变量的所有可能的组合。
涉及到的名词：
语法：命题逻辑中的公式，由常量、变量和逻辑连接符组成。两个常量符号⊤（true）和⊥(false)
- 原子是
- 一个常数 ⊤（真）⊥（假）
- 一个变量 .x 1，x2，x 3，...
- 文字是一个原子或者对应的非值¬
- 公式是一个原子或逻辑连接词对公式的应用：
- f1¬f1（非）
- f1∧f2F 1∧F2（和）
- f1∨f2F 1∨F2（或）
- f1→f2F 1→F2（单向映射）
- f1↔f2F 1↔F2（双向映射）
语义学：公式的含义是真值的一种解释，比如{X1 -> false, X2 ->true} is one possible interpretation for the formula ¬x1∧x2
如果表达式f 在解释I 下 取值为true, 则表示为 I |= f
逻辑关系：
可满足性：表达式 f 在且仅在解释 I 下为真， 称为f为可满足式 ，否则f为不满足式。
确定性：表达式f 当且仅当在解释I 下结果为真。
二重性：满足性和有效性是彼此相辅相成的
如果有办法检查可满足性，也可以用同样的办法检查确定性。所以SAT 求解器可以用来解决这两个问题。
检查满足性 和 有效性
两种方式：搜索和演绎
搜索的思路：在每一个可能的解释下，计算其结果是否为True
演绎的思路：假设f 不确定，推导所有可能的假设
一般情况下SAT的形式
三种范式
NNF 否定范式 negation normal form
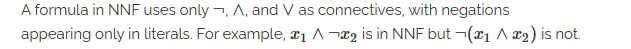
DNF 析取范式 disjunctive normal form
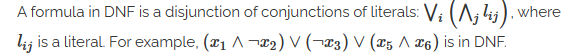
CNF 合取范式 conjunctive normal form
SAT求解器的输入是CNF,原因在于 如果将一个公式转换为等效的DNF，可能会导致复杂度呈指数增长。
FROM
