主析取范式DNF以及离散数学的一些基本概念

1、命题：能判断真假的陈述句 为命题

2、命题公式：若在复合命题中，p\q\r等不仅可以代表命题常项，还可以代表命题变项，这样的复合命题形式称为命题公式

3、命题的赋值：A为命题公式，p,p,p,....p 为A中出现的所有命题变项，给p,p,p,...p 指定一组真值，称为对A的一个赋值或者解释。如果指定的一组值 使A的值为真，则称为成真赋值

4、真值表：n个命题变项的命题公式，共有2^n组赋值，将命题公式A在所有赋值下的取值情况列成表，则称为真值表。

5、命题公式的类型：

　　a.如果A不论变项如何赋值，都取真值，则为永真式

　　b.如果A不论变项如何赋值，都取假值，则为永假式

　　c.如果A至少存在一组赋值是成真赋值，则为可满足式。

6、简单合取式：有限个命题变项或其否定构成的合取式，用^联接。

（可以理解为变项交集）

 

 7、析取范式：由有限个简单合取式组成的析取式。如：

 

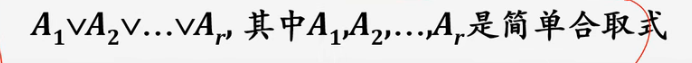
 8、极小项：满足两个条件的简单合取式

不缺项（所有变项都包括）、按顺序排好（按变项顺序排列）

9、主析取范式：由极小项构成的析取范式

比如  极小项1 V 极小项2  V 极小项3