pytorch 损失函数
损失函数在深度学习领域是用来计算搭建模型预测的输出值和真实值之间的误差。
具体实现过程：在一个批次（batch）前向传播完成后，得到预测值，然后损失函数计算出预测值和真实值之间的差值，反向传播去更新权值和偏置等参数，以降低差值，不断向真实值接近，最终得到效果良好的模型。
常见的损失函数包括：MSE（均方差, 也可以叫L2Loss），Cross Entropy Loss（交叉熵），L1 Loss（L1平均绝对值误差），Smooth L1 Loss(平滑的L1 loss)，BCELoss (Binary Cross Entropy)等。下面分别对这些损失函数举例说明。
只写了一部分，后面陆续增加。。
2.1 MSELoss
MSELoss 就是计算真实值和预测值的均方差，也可以叫L2 Loss。
特点：MSE收敛速度比较快，能提供最大似然估计，是回归问题、模式识别、图像处理中最常使用的损失函数。
import torch from torch import nn from torch.nn import MSELoss inputs = torch.tensor([1, 2, 3], dtype=torch.float32) outputs = torch.tensor([2, 2, 4], dtype=torch.float32) # MSE # size_average为True,表示计算批前向传播后损失函数的平均值，如果为False，则计算损失函数的和。 # 同样，reduce为True，返回标量；reduce为False, size_average参数失效，直接返回向量形式的loss # reduction目的为减少tensor中元素的数量。为none,表示不减少；为'sum'，表示求和；为'mean'，表示求平均值 loss_mse = nn.MSELoss() result_mse = loss_mse(inputs, outputs) print(result_mse) loss_mse1 = nn.MSELoss(reduction='sum') result_mse1 = loss_mse1(inputs, outputs) print(result_mse1) loss_mse2 = nn.MSELoss(size_average=False, reduce=False, reduction='sum') result_mse2 = loss_mse2(inputs, outputs) print(result_mse2)
2.2 L1Loss
L1Loss是计算预测值和真实值的平均绝对误差。
特点：对异常点的鲁棒性更强，但在残差为零处不可导，收敛速度比较慢。
# beta默认为1，表示指定要在L1和L2损失之间更改的阈值。 loss_smol1 = SmoothL1Loss() result_smol1 = loss_smol1(inputs, outputs) print(result_smol1)
2.3 SmoothL1loss
SmoothL1loss是L1Loss 和MSE的混合，最早在Fast R-CNN中提出。
特点：收敛速度稳定，模型更容易收敛到局部最优，防止梯度爆炸。
2.4 CrossEntropyLoss
CrossEntropyLoss表示概率分布之间的距离，当交叉熵越小说明二者之间越接近，对于高维输入比较有用。一般都需要激活函数将输入转变为（0，1）之间。
经典公式：
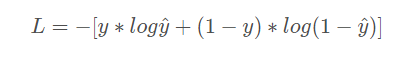
其实这个表示BCELoss（二分类交叉熵）。
pytorch的公式表示的是多分类问题：
1）当目标targets 包括类索引，ignore_index才可以设置.
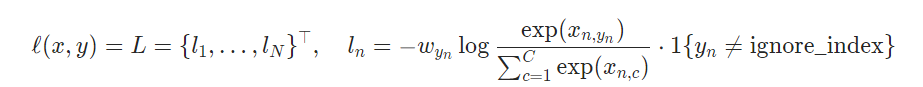
2）表示每个类别的概率；当每个小批项目需要超过单个类别的标签时非常有用，例如混合标签、标签平滑等。
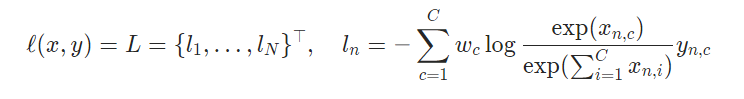
其中: x为输入值，y为目标值，C代表类别数量，w为权值参数。
# weight ：为每个类指定的手动重缩放权重。 # ignore_index：ignore_index表示指定忽略目标值，但不影响输入梯度。 # label_smoothing ：在[0.0,1.0]之间的浮点型。指定计算损失时的平滑量，其中 0.0 表示不平滑。 如重新思考计算机视觉的初始架构中所述，目标成为原始基本事实和均匀分布的混合。 # 交叉熵损失 x = torch.tensor([0.5, 0.2, 0.3]) x = torch.reshape(x, (1, 3)) print(x) y = torch.tensor([1]) loss_cross = CrossEntropyLoss() result_cross = loss_cross(x, y) print(result_cross)
交叉熵误差（cross entropy error）也经常被用作损 失函数。交叉熵误差如下式所示
这里，log表示以e为底数的自然对数（log e ）。yk是神经网络的输出，tk是 正确解标签。并且，tk中只有正确解标签的索引为1，其他均为0（one-hot表示）。 因此，式（4.2）实际上只计算对应正确解标签的输出的自然对数。比如，假设 正确解标签的索引是“2”，与之对应的神经网络的输出是0.6，则交叉熵误差 是−log 0.6 = 0.51；若“2”对应的输出是0.1，则交叉熵误差为−log 0.1 = 2.30。 也就是说，交叉熵误差的值是由正确解标签所对应的输出结果决定的。
