C语言设计实验报告(第五次)
姓名:龚政
实验地点:家
实验时间:2020.4.20
实验项目:4.3.1-1求三角形面积 4.3.1-2求阶乘 4.3.1-3求最大公约数 4.3.1-4打印三角形 4.3.2-1500以内的亲密数对 4.3.3-1x^y次幂
实验目的与要求
巩固对函数的理解,增强程序设计能力
加深递归函数的理解
符号常量的定义,局部静态变量,全局变量,定义头文件
实验内容
实验练习:4.3.1-1求三角形面积
问题的简单描述:编写程序,从键盘输人三角形的3条边,调用三角形面积函数求出其面积,并输出结果。
实验代码:
#include<stdio.h>
#include<math.h>
float area(float a,float b,float c)//海伦公式求三角形面积函数
{
float s,p,area;
s=(a+b+c)/2;
p=s*(s-a)*(s-b)*(s-c);
area=sqrt(p);
return(area);
}
int main()
{
float a,b,c,ts;
printf("请输入三角形三条边(大于零):");
scanf("%f%f%f",&a,&b,&c);
ts=area(a,b,c);
if(a+b>c&&a+c>b&&b+c>a)
printf("area=%f\n",ts);
else printf("data error!");
return 0;
}
问题分析:无
实验练习:4.3.1-2求阶乘
问题的简单描述:编写函数,求出从主调函数传来的数值i的阶乘值,然后将其传回主调函数并输出。
实验代码:
#include<stdio.h>
#define N 5//定义常数变量
long function(int i)//通过i递增计算阶乘 ,缺点是只能从1开始计算阶乘
{
static long f=1;//定义局部静态变量,这样就可以进行值传递
f=f*i;
return f;
}
int main()
{
long product;
int i;
for(i=1;i<=N;i++)
{
product=function(i);//调用函数
printf("%d的阶乘是%d\n",i,product);
}
}
问题分析:对于静态变量的理解:静态变量可以和指针一样,在函数之间进行值传递;
实验练习:4.3.1-3求最大公约数
问题的简单描述:编写程序,从键盘输人两个整数,调用gcd()函数求它们的最大公约数,并输出结果。
实验代码:
#include<stdio.h>
int gcd(int a,int b)//辗转相除法求最大公约数
{
int temp;
int remainder;
if(a<b)//交换ab,这是辗转相除法的要求
{
temp=a;
a=b;
b=temp;
}
remainder=a%b;
while(remainder!=0)//辗转相除计算最大公约数
{
a=b;
b=remainder;
remainder=a%b;
}
return b;
}
int main()
{
int x,y;
int fac;
printf("please input two integers:");
scanf("%d,%d",&x,&y);
fac=gcd(x,y);//调用函数
printf("The great common divisor is%d",fac);
return 0;
}
问题分析:无
实验练习:4.3.1-4打印三角形
问题的简单描述:输入整数n,输出高度为n的等边三角形。
实验代码:
#include<stdio.h>
void trangle(int n)//打印三角形函数
{
int i,j;
for (i=0;i<n;i++)//控制多少行
{
for(j=0;j<n-i;j++)//控制空格的输出
{
putchar(' ');
}
for(j=0;j<=2*i;j++)//控制*的输出
{
putchar('*');
}
putchar('\n');//每一行结尾的回车
}
}
int main()
{
int n;
printf("please input a integer:");
scanf("%d",&n);
printf("\n");
trangle(n);//调用函数
return 0;
}
问题分析:for(j=0;j<=2*i;j++)这样的格式是很常见的,用j来决定循环进行的次数,配合putchar,可以决定输出的个数;
实验练习:4.3.2-1 500以内的亲密数对
问题的简单描述:若正整数A的所有因子( 包括1但不包括自身,下同)之和为B,而B的因子之和为A,则称A和B为一对亲密数。
实验代码:
#include<stdio.h>
int facsum(int m)//得到因子之和函数
{
int sum=1,f=2;//初始这两个值不是绝对的,也可以是0 1;
while(f<=m/2)//f是得到m的因子,m/2是缩小因子范围,大于这个值就没有因子了
{
if(m%f==0){//判断f是不是因子,是就sum+
sum+=f;
}
f++;
}
return sum;
}
int main()
{
int m=3,n,k;
while(m<=500)//m在这里用来遍历3--500 的所有整数
{
n=facsum(m);//得到m的因子之和
k=facsum(n);//得到和(n)的因子和
if(m==k&&m<=n){//判断是否满足亲密数
printf("%d,%d\n",m,n);
}
m++;
}
}
问题分析:教材上使用的是while循环,但是可以简化成for循环;
实验练习:4.3.2-2求不定积分
问题的简单描述:利用两个文件实现跨文件调用函数
实验代码:
#include<stdio.h>
#include<math.h>
#include"sab.h"//调用本地头文件 用来求定积分的一个函数
double f(double x)//计算x*x*e^x的值
{
double result;
result=x*x*exp(x);
return result;
}
int main()
{
double a,b,result;
int n;
printf("please input double a,b and integer n:") ;
scanf("%lf,%lf,%d",&a,&b,&n);
result=sab(a,b,n);//函数调用
printf("sab(%lf,%lf,%d)=%lf",a,b,n,result) ;
return 0;
}
sab函数作为一个头文件
#include<stdio.h>
double f(double x);//函数声明
double sab(double a,double b,int n)
{
double h,result,x1,x2,x3=0,t;
h=(b-a)/n;
x1=f(a);
x2=f(b);
int k;
for(k=1;k<=n-1;k++)
{
t=a+k*h;
x3+=f(t);
}
result=h*(x1+x2)/2+h*x3;
return result;
}
问题分析:一开始没有看懂什么意思,之后才知道是两个文件!在sab.h要注意保存后缀为.h,在sab函数开头也是要声明f函数
实验练习:4.3.3-1x^y次幂
问题的简单描述:编写程序,分别从键盘输人数据x和y,计算x的y次幂并输出。
实验代码:
#include<stdio.h>
long getpower(int x,int y)//幂次方函数
{
if(y==1)//递归终止条件
return x;
else return x*getpower(x,y-1);//用到递归,表达出次方
}
int main()
{
int num,power;
long answer;
printf("请输入一个数:");
scanf("%d",&num);
printf("输入幂次方:");
scanf("%d",&power);
answer=getpower(num,power);
printf("%d^%d=%ld\n",num,power,answer);
return 0;
}
问题分析:递归函数相当于套娃,精髓也就在套娃!(滑稽)
项目实训:汉诺塔实现
设计思路
汉诺塔规则:一根柱子上从下往上按照大小顺序摞着n片圆盘。将这些圆盘移动到另外一根柱子,要求一次只能移动一个圆盘,大圆盘不能落在小圆盘上
分析:
n=1--->1步
n=2--->3步--->理解成在上一步基础上,移动了最下面一块,然后把上一步的所有圆盘移动到最下面这块上=21+1
n=3--->7步--->23+1
n=4--->15步--->2*7+1
规律:每一步都在前面基础上*2+1
hanoi函数流程图
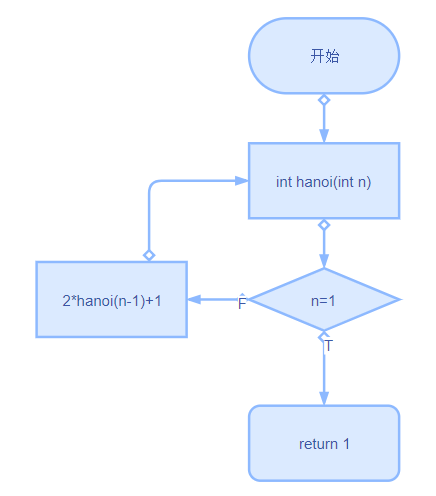
设计过程中遇到的问题及改进的方法:主要是在分析游戏过程上有问题,在写程序的时候还是很顺利的,注意递归的终止条件,这次我忘了判断是==
代码
#include<stdio.h>
int hanoi(int n)//得到汉诺塔步数
{
if(n==1)//递归终止条件
return 1;
else return 2*hanoi(n-1)+1;//递归函数得到步数
}
int main()
{
int n;
printf("请输入盘子数量:");
scanf("%d",&n);
printf("需要%d步可以完成游戏",hanoi(n));
return 0;
}

