吴恩达 深度学习笔记+作业 (一)
1.1.2 Building basic functions with numpy
1.1.2.2 numpy.exp, sigmoid, sigmoid gradient
import numpy as np def sigmoid(x): s = 1/(1+np.exp(-x)) return s
# 设sigmoid为s, s' = s*(1-s) def sigmoid_derivative(x): s = 1/(1+np.exp(-x)) ds = s*(1-s) return ds plt.figure(1) # 编号为1的figure x = np.arange(-5, 5, 0.1) y = sigmoid(x) plt.subplot(211) # 将子图划分为2行，1列，选中2行中的第1行 plt.plot(x, y) y = sigmoid_derivative(x) plt.subplot(212) # 子图中2行中的第2行 plt.plot(x, y) plt.show()
1.1.2.3 numpy.reshape(), numpy.shape
def image2vector(image): """ Argument: image -- a numpy array of shape (length, height, depth) Returns: v -- a vector of shape (length*height*depth, 1) """ v = image.reshape(image.shape[0] * image.shape[1] * image.shape[2], 1) return v
1.1.2.4 Normalizing rows
np.linalg.norm求对矩阵x按axis作向量内积
def normalizeRows(x): """ Implement a function that normalizes each row of the matrix x (to have unit length). Argument: x -- A numpy matrix of shape (n, m) Returns: x -- The normalized (by row) numpy matrix. You are allowed to modify x. """ # Compute x_norm as the norm 2 of x. Use np.linalg.norm(..., ord = 2, # axis = ..., keepdims = True) # linalg=linear+algebra. x_norm = np.linalg.norm(x, axis=1, keepdims=True) # Divide x by its norm. x = x/x_norm return x x = np.array([ [0, 3, 4], [1, 6, 4] ]) print("normalizeRows(x) = " + str(normalizeRows(x)))
1.1.2.5 Broadcasting and the softmax function
def softmax(x): x_exp = np.exp(x) s_sum = np.sum(x_exp, axis=1, keepdims=True) s = x_exp/s_sum return s
来，敲黑板：
1.np.exp(x)对任何np.array的x都可以使用并且是对每个元素进行的求指数
2.sigmoid函数以及其导数
3.image2vector在深度学习中很常用
4.np.reshape应用很广泛。保持矩阵/向量的维度会消除大量的BUG。
5.numpy有很多高效的内建函数。
6.广播非常非常有用
1.1.2 Vectorization
import time x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0] x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0] ### CLASSIC DOT PRODUCT OF VECTORS IMPLEMENTATION ###
### 向量点乘（内积）: a▪b = a^T*b （-|型）= a1b1+a2b2+......+anbn
tic = time.process_time() dot = 0 for i in range(len(x1)): dot += x1[i]*x2[i] toc = time.process_time() print("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms") ### CLASSIC OUTER PRODUCT IMPLEMENTATION ###
### 向量叉乘（外积）: axb = a*b^T (|-型)
tic = time.process_time() outer = np.zeros((len(x1), len(x2))) # we create a len(x1)*len(x2) matrix with # only zeros for i in range(len(x1)): for j in range(len(x2)): outer[i, j] = x1[i] * x2[j] toc = time.process_time() print("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms") ### CLASSIC ELEMENTWISE IMPLEMENTATION ###
### 向量元素依次相乘
tic = time.process_time() mul = np.zeros(len(x1)) for i in range(len(x1)): mul[i] = x1[i] * x2[i] toc = time.process_time() print("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms") ### CLASSIC GENERAL DOT PRODUCT IMPLEMENTATION ###
###
W = np.random.rand(3, len(x1)) # Random 3*len(x1) numpy array tic = time.process_time() gdot = np.zeros(W.shape[0]) for i in range(W.shape[0]): for j in range(len(x1)): # W的每一行与x1相乘 gdot[i] += W[i,j]*x1[j] toc = time.process_time() print("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
输出：
dot = 278 ----- Computation time = 0.00854900000035741ms outer = [[81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0. 0.] [18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0. 0.] [45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [63. 14. 14. 63. 0. 63. 14. 35. 0. 0. 63. 14. 35. 0. 0.] [45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [81. 18. 18. 81. 0. 81. 18. 45. 0. 0. 81. 18. 45. 0. 0.] [18. 4. 4. 18. 0. 18. 4. 10. 0. 0. 18. 4. 10. 0. 0.] [45. 10. 10. 45. 0. 45. 10. 25. 0. 0. 45. 10. 25. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]] ----- Computation time = 0.12781600000000282ms elementwise multiplication = [81. 4. 10. 0. 0. 63. 10. 0. 0. 0. 81. 4. 25. 0. 0.] ----- Computation time = 0.018939999999911805ms gdot = [21.88386459 17.22658932 13.05841111] ----- Computation time = 0.07001299999975785ms
numpy实现
import time import numpy as np x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0] x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0] ### VECTORIZED DOT PRODUCT OF VECTORS ### tic = time.process_time() dot = np.dot(x1, x2) toc = time.process_time() print("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms") ### VECTORIZED OUTER PRODUCT ### tic = time.process_time() outer = np.outer(x1, x2) toc = time.process_time() print("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms") ### VECOTRIZED ELEMENTWISE MULTIPLICATION ### tic = time.process_time() mul = np.multiply(x1, x2) toc = time.process_time() print("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms") ### VECOTRIZED GENERAL DOT PRODUCT ### W = np.random.rand(3, len(x1)) tic = time.process_time() gdot = np.dot(W, x1) toc = time.process_time() print("gdot = " + str(gdot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
输出：
dot = 278 ----- Computation time = 0.17038700000027163ms outer = [[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0] [18 4 4 18 0 18 4 10 0 0 18 4 10 0 0] [45 10 10 45 0 45 10 25 0 0 45 10 25 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [63 14 14 63 0 63 14 35 0 0 63 14 35 0 0] [45 10 10 45 0 45 10 25 0 0 45 10 25 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [81 18 18 81 0 81 18 45 0 0 81 18 45 0 0] [18 4 4 18 0 18 4 10 0 0 18 4 10 0 0] [45 10 10 45 0 45 10 25 0 0 45 10 25 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]] ----- Computation time = 0.1971060000003355ms elementwise multiplication = [81 4 10 0 0 63 10 0 0 0 81 4 25 0 0] ----- Computation time = 0.06556499999987864ms gdot = [19.3061823 18.29576413 24.1581206 ] ----- Computation time = 0.06616899999967174ms
As you may have noticed, the vectorized implementation is much cleaner and more efcient. For bigger vectors/matrices, the differences in running time become even bigger.
这里意思是numpy的向量化实现更加简洁和高效，对于更庞大的向量和矩阵，运行效率会相差更多。
然鹅我运行出来明明是numpy运行时间更多一丢丢。。。估计和我的环境有关系？？？
那么先不管了，接着刚下面的。。。
1.1.3.1 Implement the L1 and L2 loss functions
那么L1就是个这： 
L2就是个这：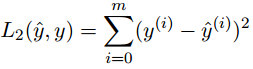
这里都是范式的概念，L1假设的是模型的参数取值满足拉普拉斯分布，L2假设的模型参数是满足高斯分布，所谓的范式其实就是加上对参数的约束，使得模型更不会overfit，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。
贴代码：
import numpy as np # GRADED FUNCTION: L1 def L1(yhat, y): """ Arguments: yhat -- vector of size m (predicted labels) y -- vector of size m (true labels) Returns: loss -- the value of the L1 loss function defined above """ loss = sum(abs(y-yhat)) return loss # GRADED FUNCTION: L2 def L2(yhat, y): loss = np.dot(y-yhat, y-yhat) return loss yhat = np.array([.9, 0.2, 0.1, .4, .9]) y = np.array([1, 0, 0, 1, 1]) print("L1 = " + str(L1(yhat, y))) print("L2 = " + str(L2(yhat, y)))
来，敲黑板：
1.向量化在深度学习中灰常重要，TA使计算更加高效和明了。
2.回顾了L1和L2 LOSS。
3.熟悉了numpy的np.sum, np.dot, np.multiply, np.maximum等等。
接着刚1.2
1.2 Logistic Regression with a Neural Network mindset
那么在这一节我们要开始第一个深度学习的练习了。在这里将会build你的第一个图像识别算法----猫子分类器，70%的acc哦~
那么在这里完成作业以后你将会：
用logistic回归的方式构建神经网络。
学习如何最小化代价函数。
明白如何对代价函数求导来更新参数。
Instructions:
不要在代码中使用循环(for/while)，除非instructions明确的让你这么做。
你将会学到：
构建一个一般的学习算法，包括：
-初始化参数
-计算代价函数及其梯度
-使用一个优化算法（梯度下降）
在main函数里面正确的使用以上三个函数。
1.2.1 Packages
先来介绍几个包：
numpy: python里面的一个科学计算基础包
h5py: 和存储为H5文件的数据集做交互的通用包
matplotlib: python里面一个很屌的绘图库
PIL: 在这里用来对你自己的图片在最后进行测试（其实就是个图像库）
1.2.2 Overview of the Problem set
问题表述： 给定一个数据集"data.h5", 其中包括：
*标有cat(y=1)或non-cat(y=0)的训练集
*标有cat或non-cat的测试集
*每张图片为(num_px, num_px, 3)的shape，其中3代表3通道(RGB)，图片是方形，高num_px宽num_px
贴一波代码：
import numpy as np from matplotlib import pyplot as plt import h5py import scipy from PIL import Image from scipy import ndimage from lr_utils import load_dataset #matplotlib inline # Loading the data (cat/non-cat) train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes =\ load_dataset() # Show datasets' shapes m_train = train_set_x_orig.shape[0] m_test = test_set_x_orig.shape[0] num_px = train_set_x_orig.shape[1] print("Number of training examples: m_train = " + str(m_train)) print("Number of testing examples: m_test = " + str(m_test)) print("Height/Width of each image: num_px = " + str(num_px)) print("Each image's size is: (" + str(num_px) + ", " + str(num_px) + ", 3)") print("train_set_x shape: " + str(train_set_x_orig.shape)) print("train_set_y shape: " + str(train_set_y.shape)) print("test_set_x shape: " + str(test_set_x_orig.shape)) print("test_set_y shape: " + str(test_set_y.shape)) # Reshape dataset's shape (209, 64, 64, 3) to shape (209, 64*64*3) train_set_x_flatten = \ train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T test_set_x_flatten = \ test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T print("train_set_x_flatten shape: " + str(train_set_x_flatten.shape)) print("test_set_x_flatten shape: " + str(test_set_x_flatten.shape)) print("sanity check after reshaping: " + str(train_set_x_flatten[0:5, 0])) # Visualize an example of a picture index = 25 plt.imshow(train_set_x_orig[index]) print("y = " + str(train_set_y[:, index]) + ", it's a '" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' picture. '") plt.show()
敲黑板：
一般对一个新数据集进行预处理的步骤为：
* 找出问题的dimensions和shapes(m_train, m_test, num_px, ...)
* 将数据集reshape使每个样本都成为一个向量，大小为(num_px * num_px *3, 1)
* 标准化数据
1.2.3 General Architecture of the learning algorithm
下图解释了为什么 Logistics回归是一个非常简单的神经网络：
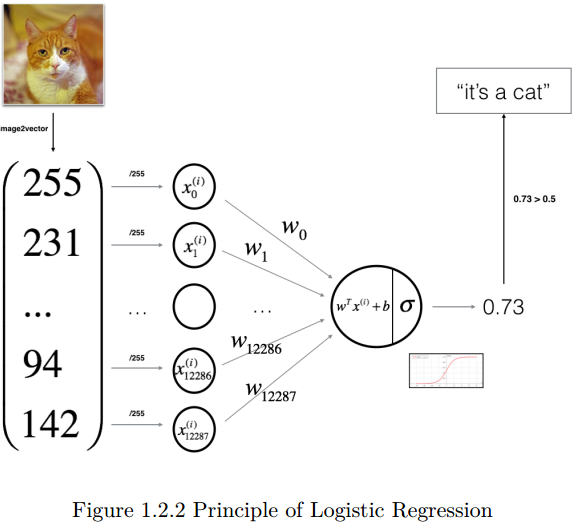
该算法的数学表达：
对于每一个样本x(i):
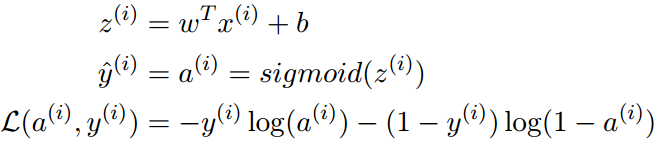
这里的L其实是，每一个样本看做一次伯努利实验，那么分布就是0-1分布，那么对这个0-1分布求极大似然估计就是...贴一波《统计学习方法》的推导：
吴恩达在这里的L函数其实是统计学习方法中的对数似然函数取负的其中一项。
那吴恩达在这里给出的代价函数为：
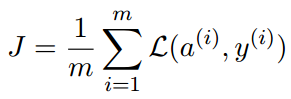
那么可以看到他这个代价函数J其实就是对《统计学习方法》中给出的似然函数取负并归一化了一下（除以m）。
那么接着往下刚。。。
Key steps:
* 初始化模型参数
* 通过最小化代价函数学习模型参数
* 使用学习到的参数来做预测（在测试集上）
* 分析结果并得出结论
1.2.4 Building the parts of our algorithm
构建一个神经网络的主要步骤有：
* 定义模型架构（如输入features的个数）
* 初始化模型参数
* 循环：
- 计算当前的损失（前向传播）
- 计算当前的梯度（反向传播）
- 更新参数（梯度下降）
通常将1-3步分别实现并集成在一个model()函数里。
1.2.4.1 Helper functions
