混合积、立体角与几何体体积

观前提醒：请先阅读前文，否则可能出现理解上的断层

Part 1：混合积及其"轮换"对称性

混合积，顾名思义，就是把数量积和向量积混合起来；考虑到是向量运算，故必然是先向量积后数量积。

混合积记做 [a b c] ，其值为 (a×b)·c

且有：

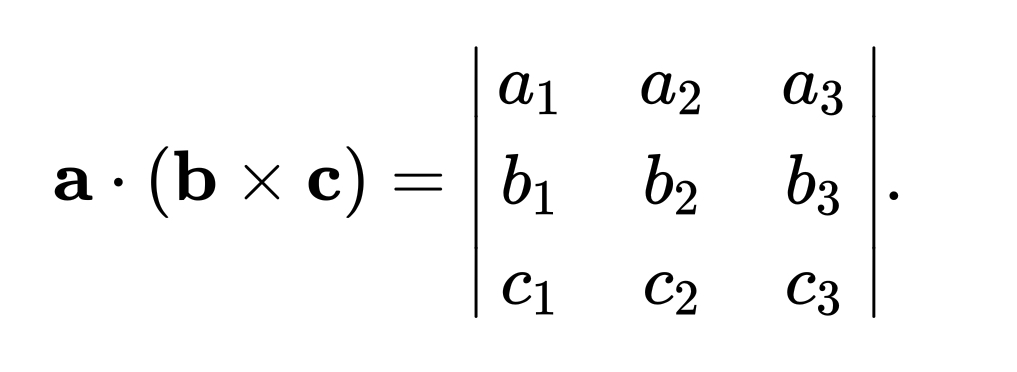
这点可以从数量积和向量积的计算公式中推导出来 

不难发现，(a×b)·c = (b×c)·a = (c×a)·b ，即如果保持abc、bca、cab的顺序，只是将其轮换，其混合积的值不变，这一点可以任意举例证明，不过结合下文内容，可以更好的理解这一性质。

P.S.:标题中"轮换"对称性这个名字不一定准确，仅仅作为形象的说法

Part 2：混合积的几何意义

 先放张图：

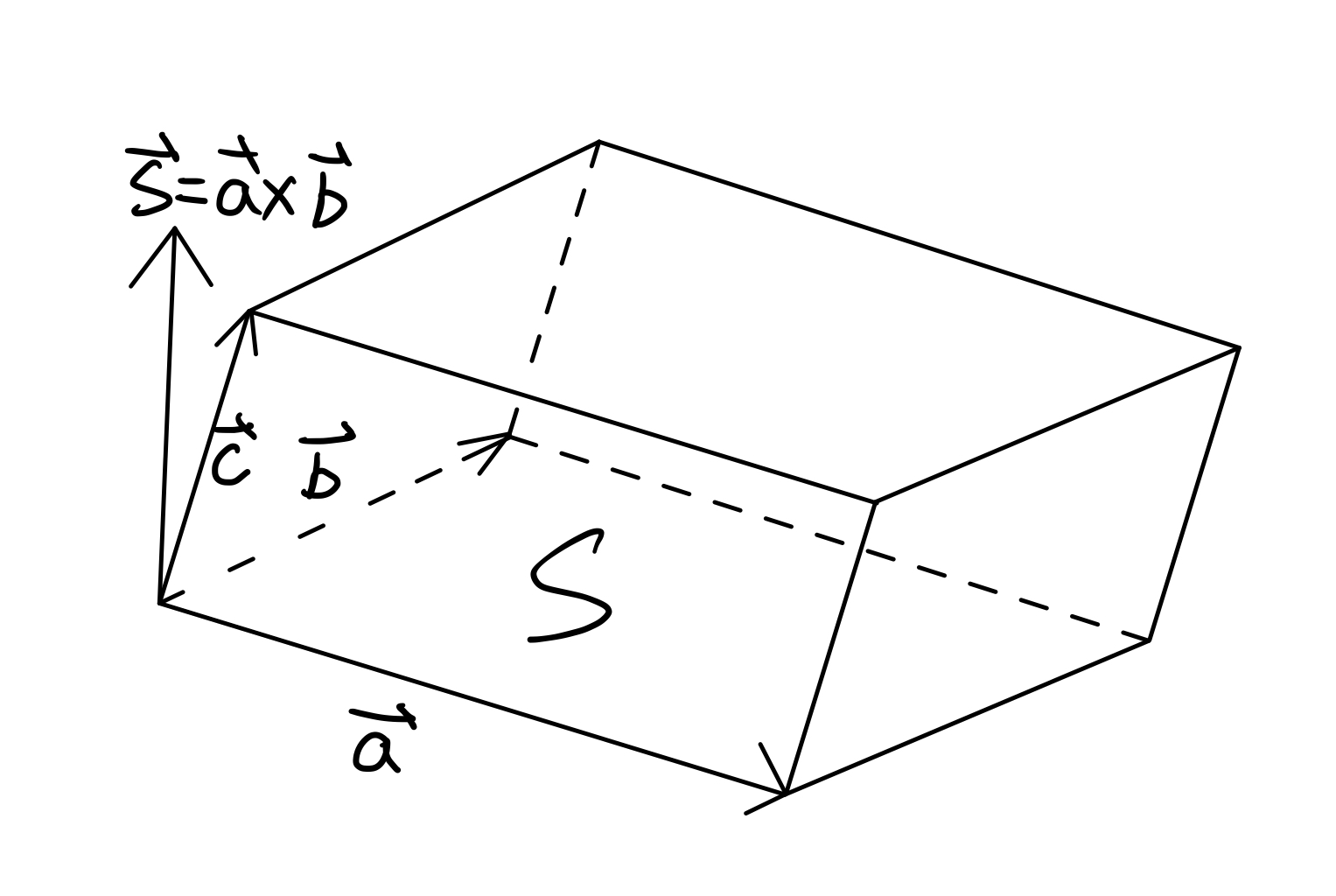
(本图可能相对下文的图效果较差，别问为啥，问就是noteability试用过期了）

可以看出，如果 a x b 与 c 在底面的同一侧，则 V = (a×b)·c =  [a b c] 

考虑更一般的情况，若 a、b、c 为平行六面体同一顶点"发出"的三根边，则其体积 V =  | [a b c] |

且若三个向量构成右手系（类比空间右手直角坐标系），去掉绝对值后取正，构成左手系取负值。

这样，我们就能理解上文中的性质了：经过"轮换"后三个向量构成的是左手系还是右手系不变，正负性不变；由于其对映的平行六面体体积不变，故其绝对值亦是不变的。

聪明的读者可能已经发现，我们没有考虑混合积为零的情况。显然，由于平行六面体的体积为0，三个向量共面。因此，计算混合积的值是否为0，是判断三向量是否共面的方法之一。（总比待定系数法解设简单吧？）当同学们未来学习了线性代数相关知识后，还会对此有更深层次的理解。

Part 3：立体角

这块知识较为简短，懒得单独开一个模块了，故直接放在同一篇

高一的时候我们学过，平面中、弧度制下角的定义是圆弧/圆半径

类似的，空间中，角可以定义为"球冠"面积除以球体半径的平方，单位是球面度sr。

不清楚的同学可以点击链接了解什么是球冠（不会吧，不会还有高中生不知道吧？）

如下图：

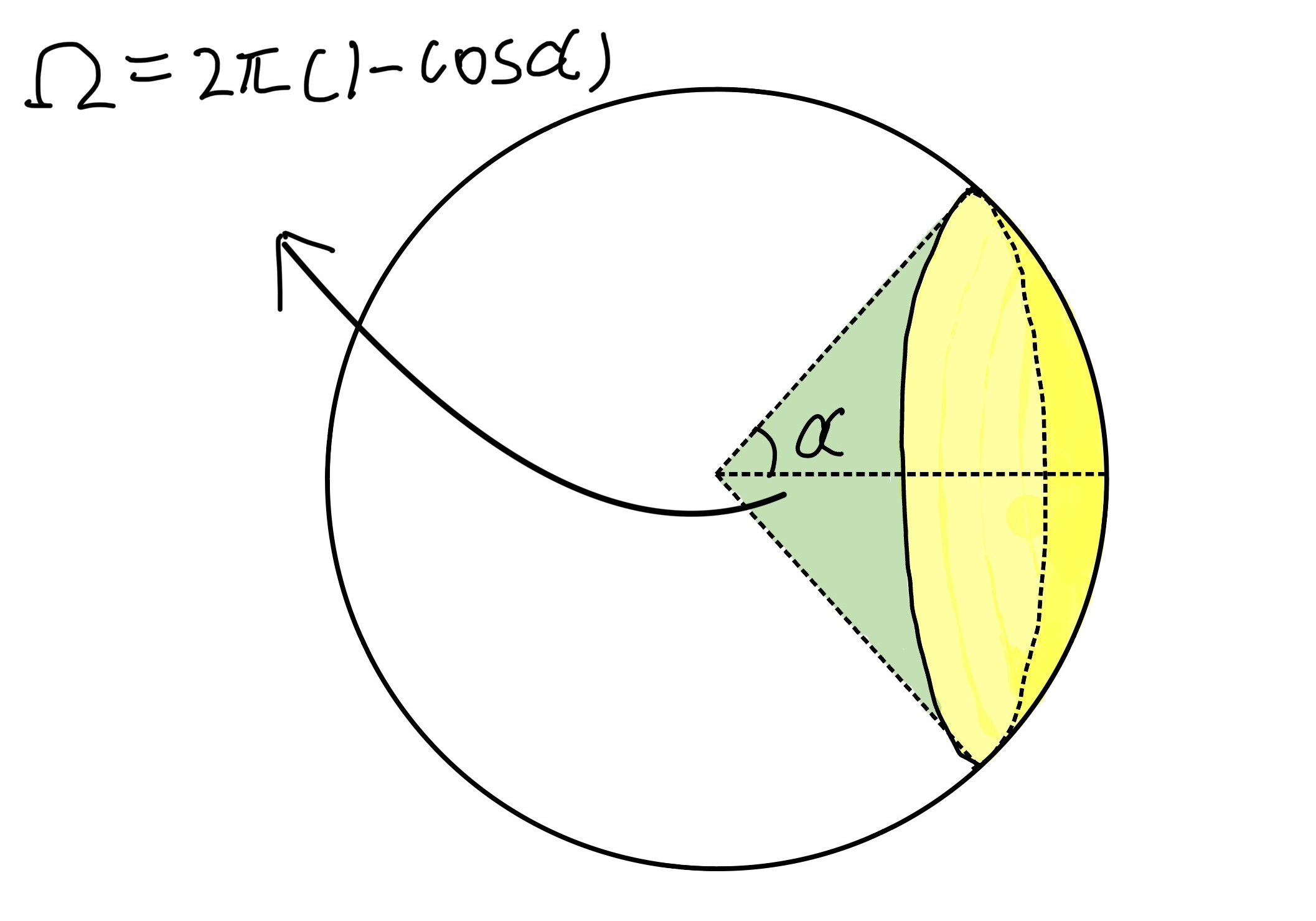
 其中 Ω 指的是立体角，α 是边界上半径与中轴上半径所夹的平面角。

不用去管图中公式哪里来的，问就是二重积分，大家应该没学到，这个结论记住就行了。

如果怕自己记错公式里的正负号，把 α = 0 和 pi 带进去试一下来检验就行了。

显然，有关系：球冠面积 S = Ω·R^2（图中已用黄色标出）

事实上，立体角不一定非得是图中“圆锥形”，完全可以“歪歪扭扭”，只是此时求角的大小会变得更加复杂，因此不展开论述了。

Part 4：一些几何体体积的求法

书接上回，想到扇形面积公式 S = （α·R^2）/2，不难猜出"扇体"体积 V = （Ω·R^2）/3

其中"扇体"这个名字是我编的，有知道真实名称的同学可以留个言，指的是上图中绿色和黄色所围成的区域。

此外，从这个二分之一和三分之一可以看出，额外的系数恰好是维度的倒数，这一点学习了积分后大家会有更深层次的理解（又在画饼了是吧）

省锡中的2021年入学的同学们或许会发现，这不正跟高一下学期数学期末单选最后一道题一样嘛，学了这种方法，题干都不用读，直接秒杀！

另外，从混合积的几何意义可以推测，混合积同样可以用来求三棱锥的体积，方法是从三棱锥的边上找三个矢量，取混合积后除以二，再取绝对值。

第一种方法，取从同一顶点发出的三条边，如下图：

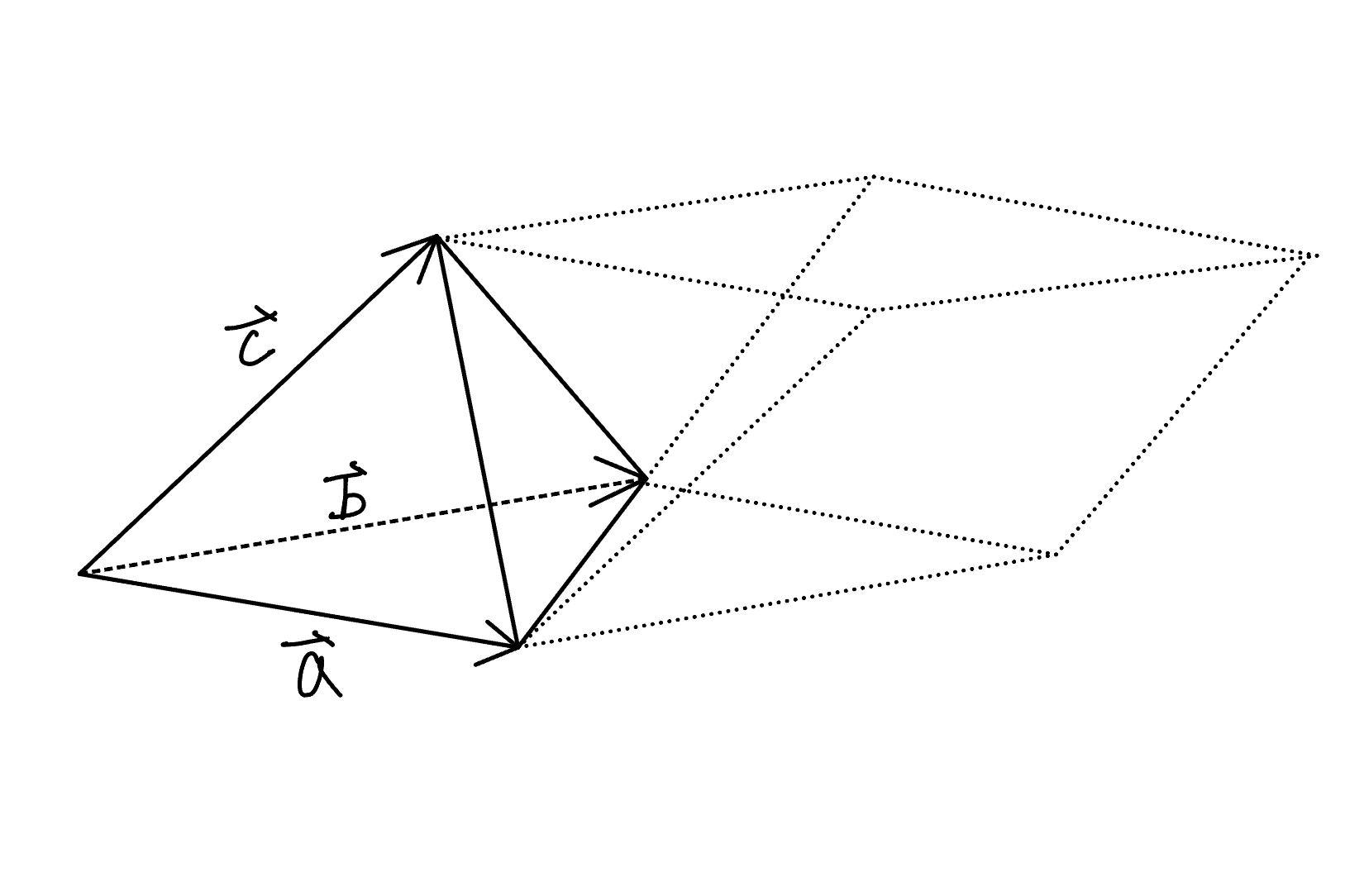
这还是比较显然的。

第二种是取三条顺次链接的边，但不能形成闭合的三角形，如下图：

 

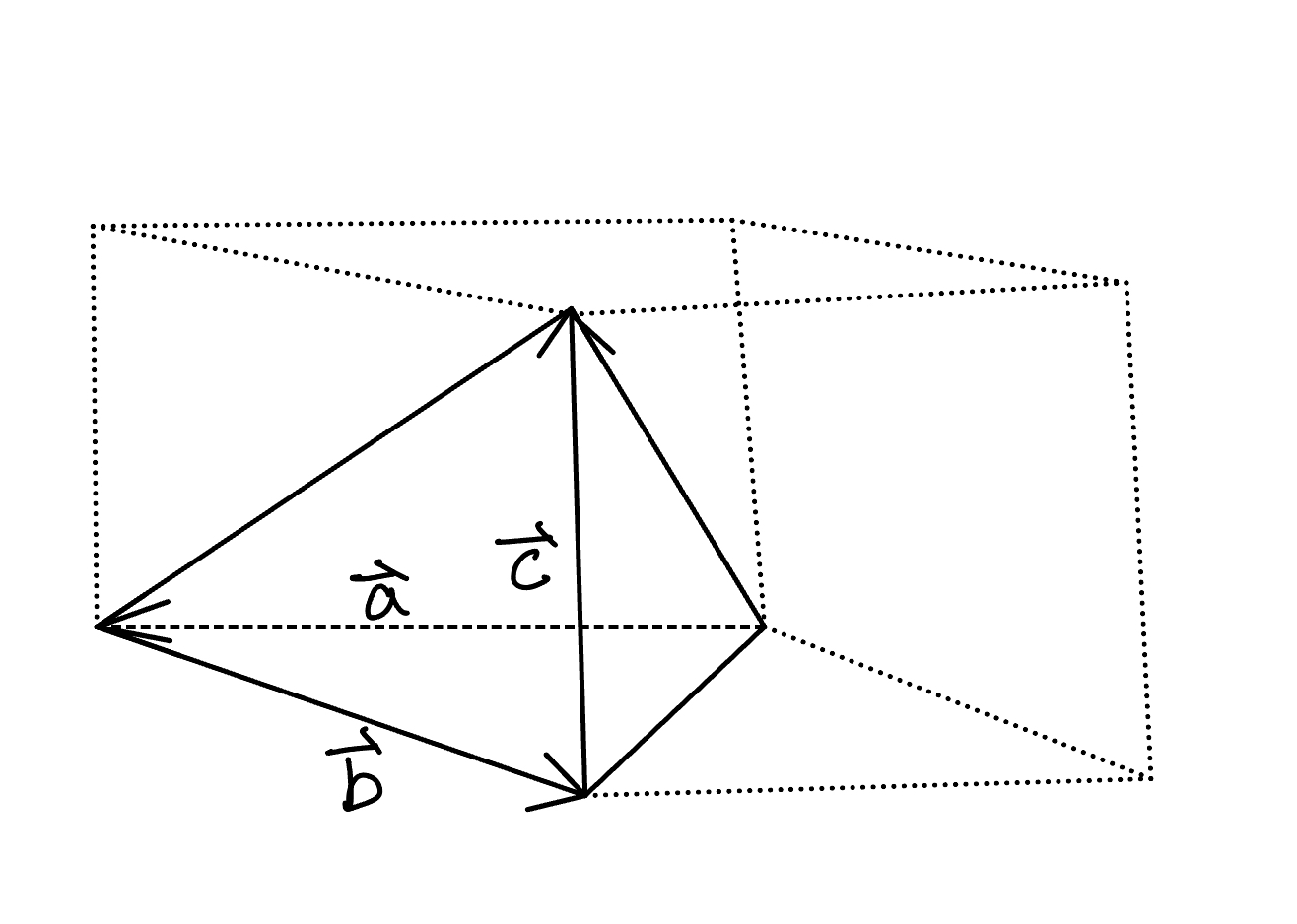
 Amazing 啊！是不是非常简单呢？（手动狗头）