向量积、“伪”矢量与电磁力

写作目的详见这个

阅读本文建议使用亮色背景！

这个标题或许会让人疑惑，这三个东西是如何联系在一起的，以及，什么是“伪”矢量？

相信读完本文，你一定会有许多收获，那些关于安培力、库仑力...该举起哪只手的疑惑也将迎刃而解！

观前提醒：请先阅读上一篇关于行列式的文章！

Part1：什么是向量积？

我们在高中阶段学过点乘，又被称为内积或数量积。数量积的值是一个数，可以合理的推知，向量积的结果是个向量（废话）

先定这个向量的模，由于数量积的系数取的是cosθ，这边相反，取sinθ，有：

至于方向，显然不应该在两个向量确定的平面内（往哪偏都不合理啊），应该垂直于两向量所确定的平面（若a、b、sinθ有其中之一为零，则结果为0向量）

为确定指向，方便起见，不妨让三个向量共起点，然后有如下法则：

举出右手，“握住”a、b所确定平面过起点的法向量，四指先”穿过”a，再穿过b，若转过的角度小于π，则方向为大拇指所指方向；否则，则为大拇指反方向，如下图

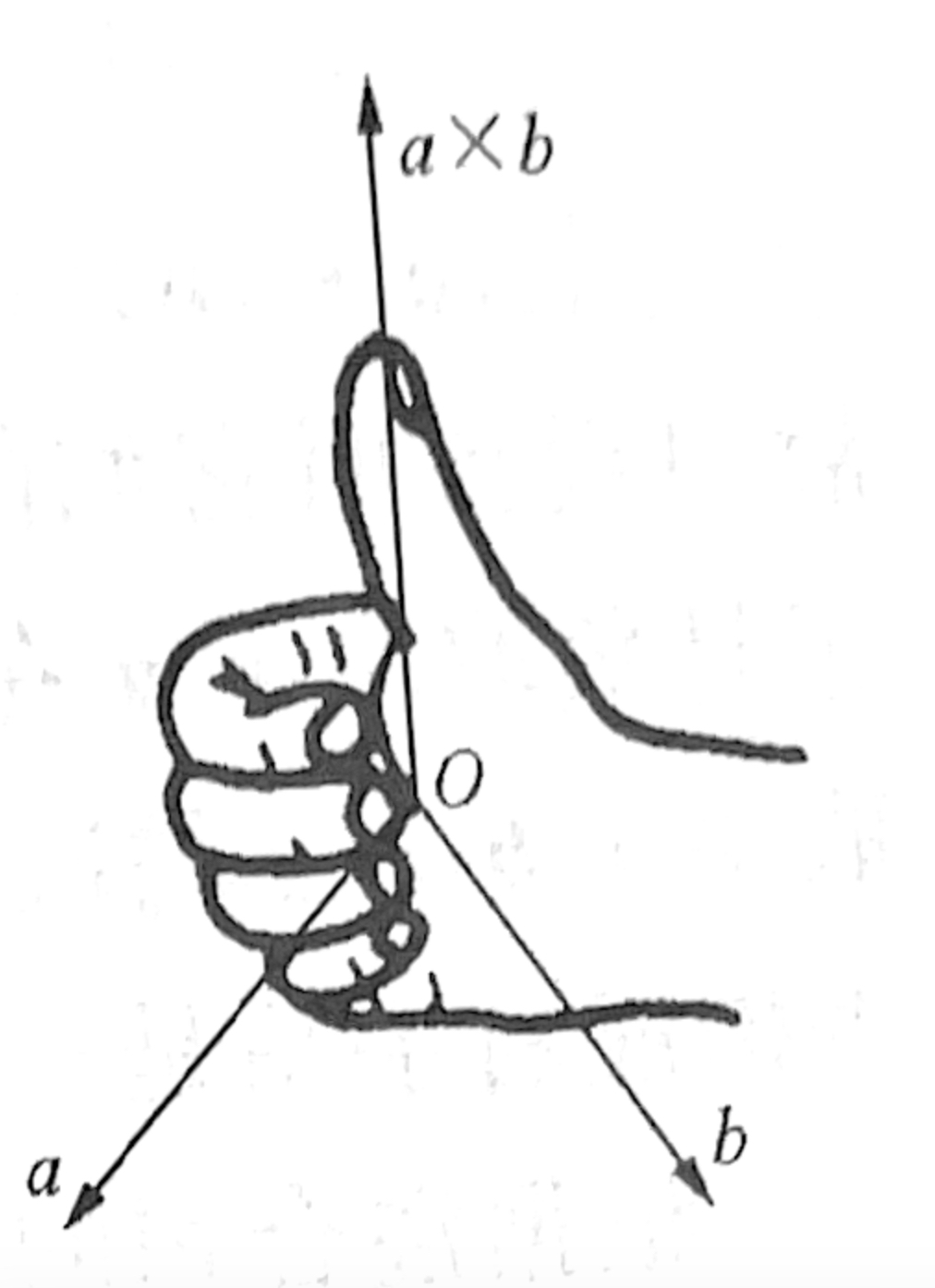
 在右手空间直角坐标系中，向量积还有更简单的计算方法，如下图（对齐方式有点阴间，不要去管它）

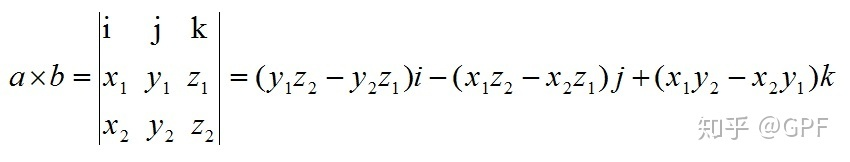
其中，i、j、k是x、y、z正方向上的单位向量，且记 a = ( x₁ , y₁ , z₁ ) , b = ( x₂ , y₂ , z₂ )

老师要求我们建立右手系而不是左手系，正是因为在左手系中，利用行列式法算出来的指向和正确结果是相反的，虽高中阶段未教学向量积，但这种建系方法应成为一种习惯。

顺便一提，在上式中，行列式计算出来的是一个矢量，而非前文中所提及的一个值。严格来说，这种做法背离了行列式的原本意义，在此处是为了记忆方便，对行列式的运算法则进行了推广。

从上文可知，叉乘的前后两矢量具有顺序，因此叉乘不满足结合律与交换律，且a x b = - b x a

当然，容易发现，叉乘是满足分配律的，因此可利用分量形式来更便捷的计算叉乘。

Part2：向量积的几何意义与伪矢量

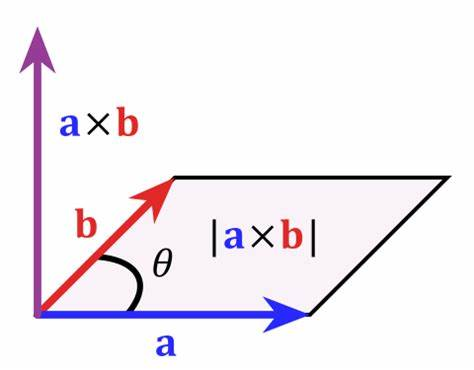
观察向量积模的表达式，可以发现模恰好等于以a，b为邻边的平行四边形的面积（如上图），这便是它的几何意义。

我们可以利用这一性质加上 a x b 的行列式计算法在坐标系中快速求得空间三角形的面积，大多数情况下会比海伦公式快不少。

同时，我们也可以把 a x b 所得矢量称为该平行四边形（按上图a——b——（-a）——（-b）(即逆时针)绕行方向）的面积矢量。

有的同学可能会感到疑惑，面积通常意义上是标量，面积矢量的方向性有何意义呢？
确实，面积矢量的方向性的意义不强，可以理解为它的方向性是人为定义的，目的是方便如磁通量等的运算：

这样子写，是不是省事多了？

像这样，通过两个矢量叉乘来定义出矢量p，称p为伪矢量，又名赝矢量，因其不具有一般矢量明晰的方向意义（不严谨，详见百度百科）

比如，角速度矢量，就是通过径矢r叉乘速度v除以r^2得到的，如下图：

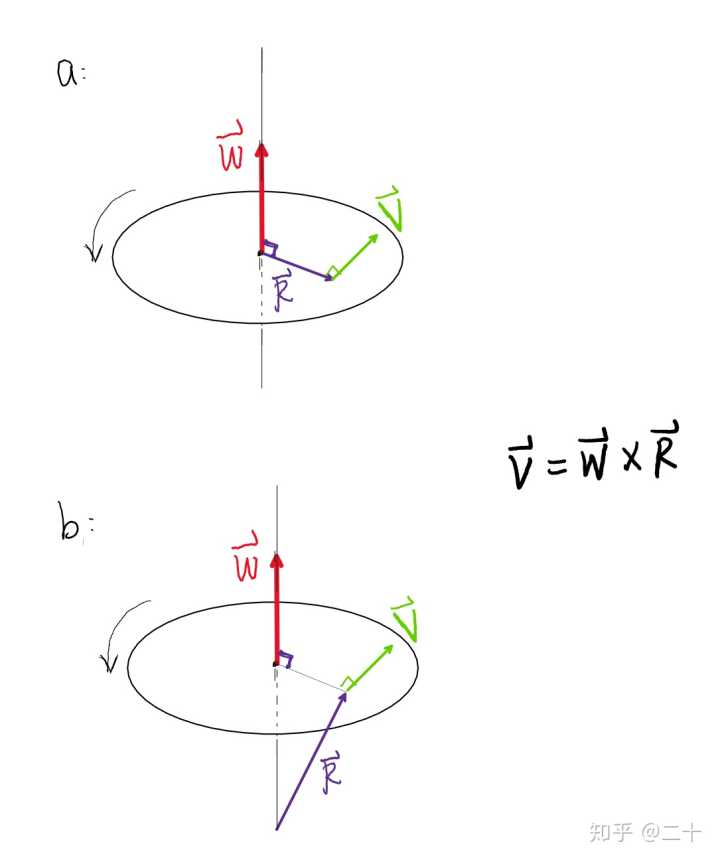
图中是反过来定义的，找出ω使得 v = ω x r ，结果仍是一样的，只不过思路不同。

如此，便可便捷地用一个矢量表达整个物体旋转的方向、角速度。

同样的，磁感应强度，角动量等也属于伪矢量。

与一般的矢量相仿，伪矢量相加也满足平行四边形法则，如此便可以处理旋转叠加等问题。

Part3：向量积在电磁学中的运用

安培力是磁场作用在通电导体上的力，而洛伦兹力是磁场作用于运动带电粒子的力，由于电流是由带电载流子运动形成的，故洛伦兹力是安培力的微观本质，二者的表达式本质上也是等价的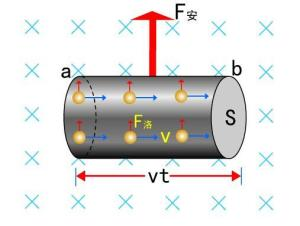                 

后文假定您对这两种力有一定了解，如对其所知不多清先阅读人教版高中物理选择性必修二的第一章

这里直接放结论：

安培力满足   

 

其中F，L，B为矢量，L方向为电流方向（L大写是为了区分），I不是矢量，后面加了一点是为了隔开好看而不是指代数量积！

同样的，洛伦兹力满足   ，这里的q要保留正负号。

观察这两个式子，可以发现表示电流/带电粒子的矢量总是写在" x "号前面，这样就能轻松判断这两个力的方向啦！

说明一下，这里不用总是把B放在后面来记忆是为了使这一规律更具普适性，因为在毕奥——萨伐尔定理中，有：

(找不到带白色背景的图了，将就一下)

用来从给定的电流求出任意一点的磁感应强度。

其中前面那个系数的大小为1，单纯是为了统一单位；L方向为电流元方向

d在进入导数篇前可以暂且理解为Δ，表示微小的增量（因为电流元到所给点的位矢往往会不断变化，故采取小量形式）

注：这个定理不用掌握，其只是拓展。由于高中阶段不用求磁感应强度大小，方向的判断用右手螺旋之类的定理更方便。(也是只要用右手啊)

可以发现，在引入向量积后，我们只需要用到右手便能解决问题，方便多了。