行列式的简介

写作目的详见这个

注：本文介绍行列式的目的是为了方便记忆与运算，不涉及其本质，想了解更多的同学可以看看这个系列视频

一般的行列式长这样：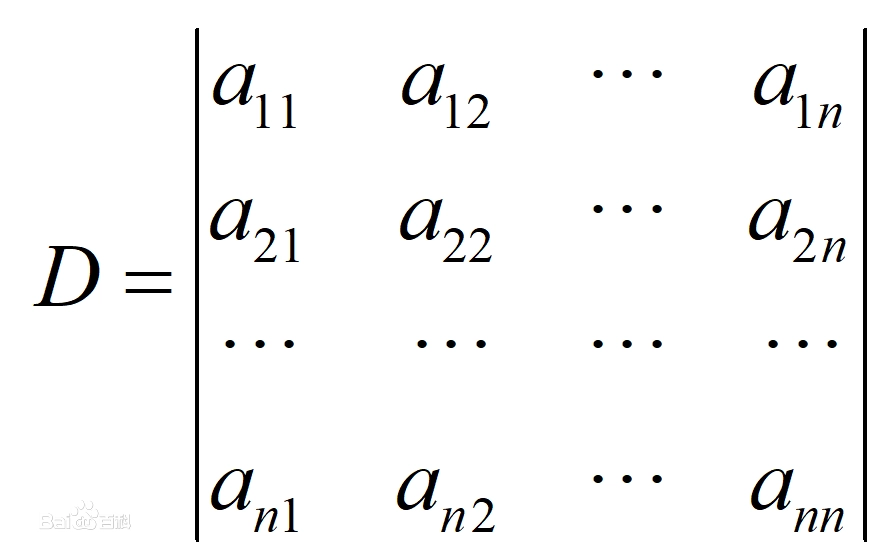

 

它一个n*n的有序数组和一对”绝对值号“构成（称为n阶行列式）。

我们可以暂且把它理解为一种特殊的函数，输入n^2个数字，输出一个数（即行列式的值）

行列式的计算

那么，该怎么求出它的值呢？

我们不妨从最简单的情况开始。

一阶行列式得知就是那个数本身。

二阶行列式及其求法是这样的：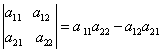

 

 可以看出，二阶行列式的值是左对角线的乘积减去右对角线。

可以上百度看看它最基本的用途：快速解二元一次方程。

说句题外话，其实行列式一开始被发明出来的目的就是解多元一次方程（即线性方程），只是后来其用途被推广了

至于三阶行列式,有，两种算法。

第一是展开成二阶行列式：

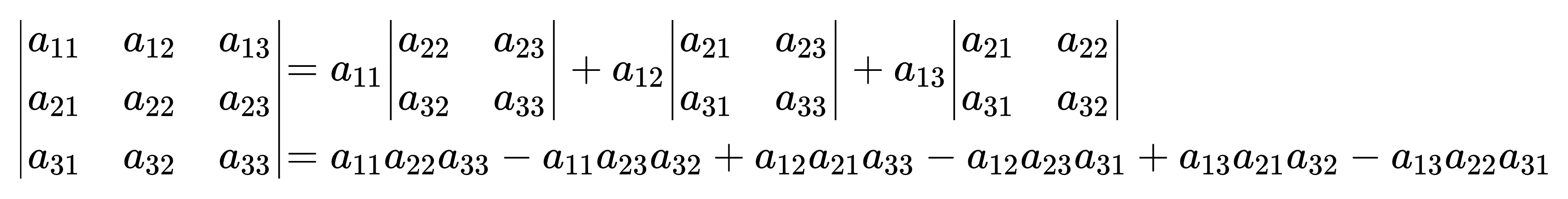
（emmmmm，两个等号之间的式子中间加号应该改为减号，图片就不重新弄了） 

直接算也行，记忆方法如下图：（图片有点草，但这并不重要）

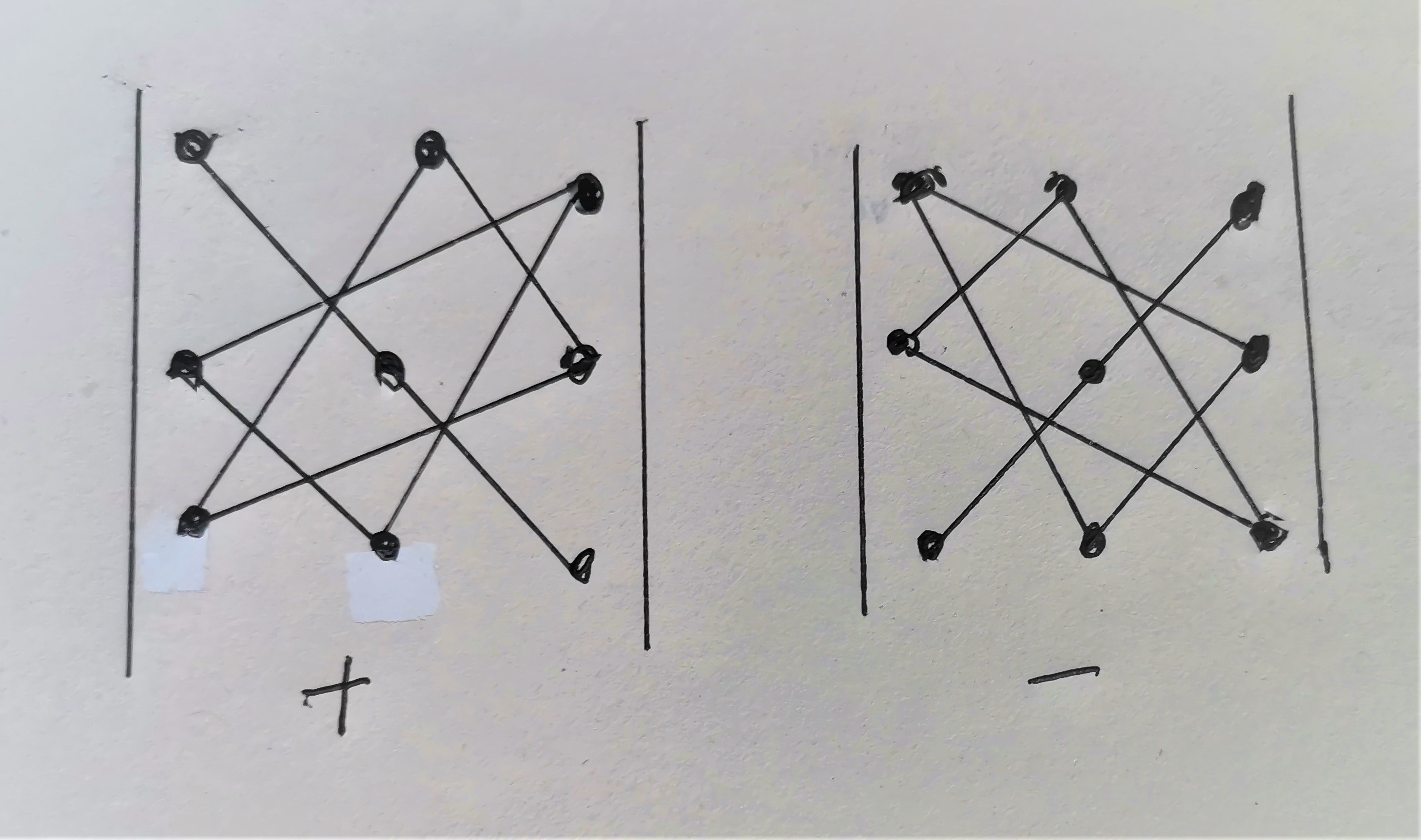
计算方法是将左图连起来的三组数每组相乘后加起来再减去右图中每组相乘加起来的值
可能有同学没有看懂，可以对比上面的式子进行理解。

至于更高阶的行列式，多用逐阶展开进行计算，在此略过不提，可以自行查阅。

运算性质

 最后讲一个运算性质吧。

行列式具有对角线对称性，这意味着将数字排列按照对角线镜像”翻折“后，行列式的值不变。

大家可以自行对二阶和三阶的情况进行验证。

由于个人习惯，有人写行列式是横着写（类比现代汉语写法），有人竖着写（类比古代汉语书籍，如圣旨，但是竖排排列顺序要变为从左往右），但由于以上性质，算出来行列式的值是相同的。