NJU软件分析笔记(3)
NJU Static Analysis Notes(3)——Data Flow Analysis Ⅱ
课程链接
本次课程主要内容
- Live Variables Analysis
- Available Expressions Analysis
活跃变量分析
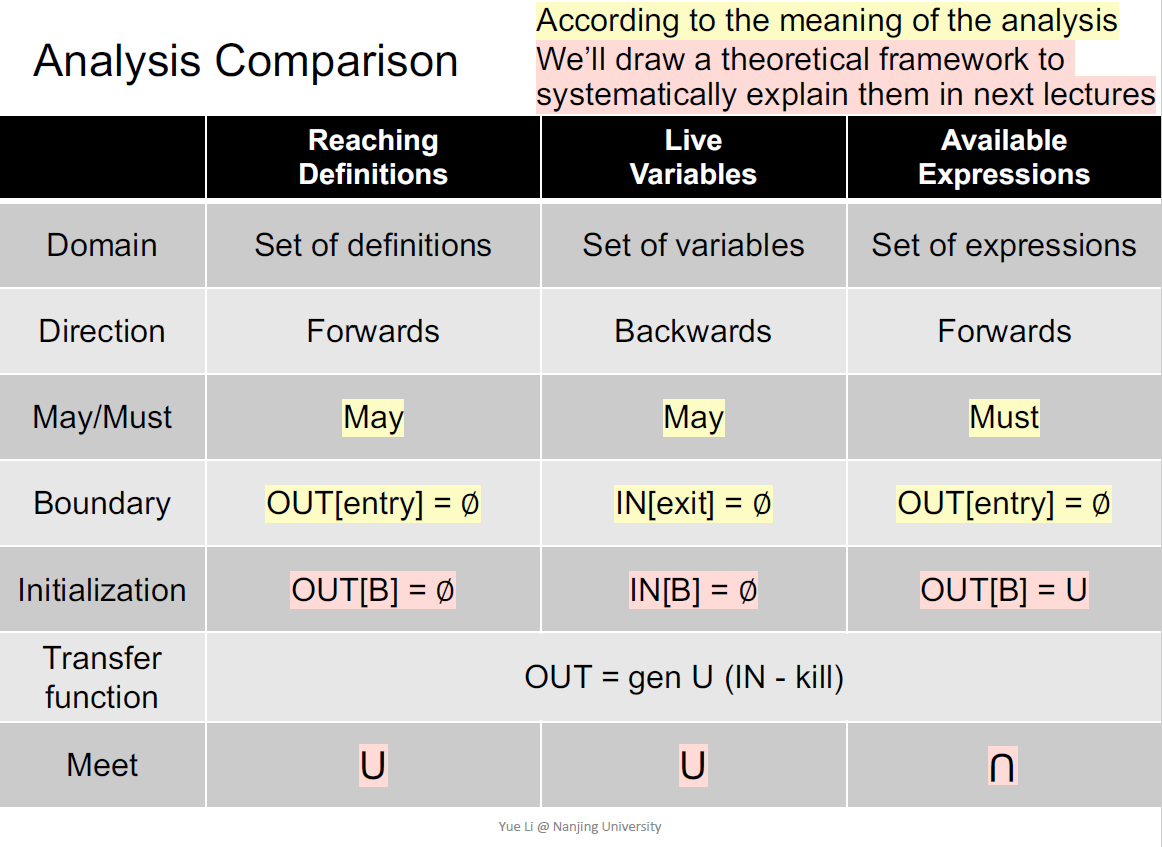
活跃变量(live variable)分析的作用在于,能告知我们在某个程序点p的变量值v能否在CFG中沿着某条以p为起点的路径一直往后传播(may-approximation)。如果能做到则说v在p是活跃(live)的,否则说v是死(dead)的。

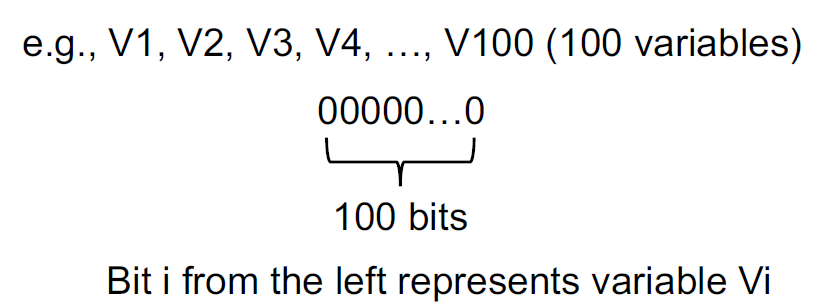
所以这条路径上v不能被redefine。活跃变量分析的一个用途就是寄存器分配,在寄存器满的情况下如何选择合适的寄存器替换,按上面的定义应该选一个dead的值。同样按照以前的抽象,采用位向量表示每个变量是否live。
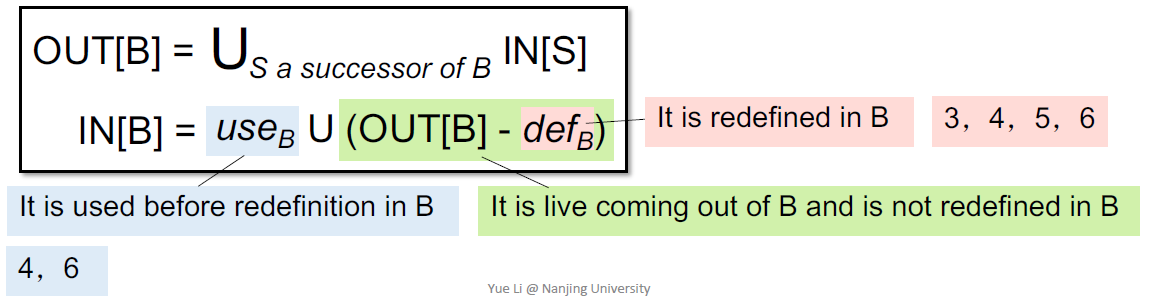
思考这个问题的目的所在,一个好的分析方法是backward进行。即通过OUT去计算IN:
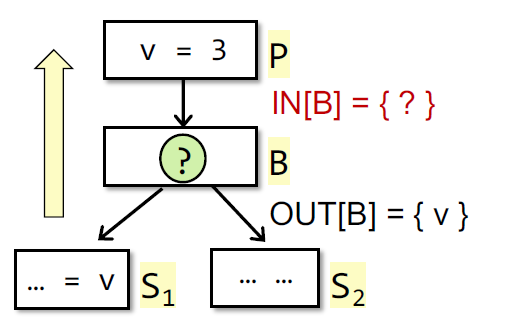
这里因为S1中使用了v,所以OUT[B]包含{v}, 也就是说在这一点(B之后)v是live的,那么通过这个B之前的情况如何呢?有哪些变量在B中被使用(useB),有哪些在B中被定义(defB),这些都影响到IN[B]的值。

所以这里我们的transfer function和control flow可以写为:

理解上,如果OUT[B]中含有某个变量z,但是B中有定义z=... 很显然在B之前的程序点,z不应该为live,因此OUT[B]-defB,而如果B中使用了m,那么在B之前的程序点m是live的因此并上usedB。需要注意的一种情况是,针对某个变量既有used也有def,那么就要根据顺序分析。
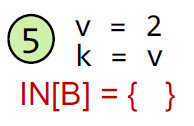
因为先定义后使用,所以v被删去;
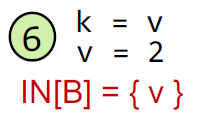
因为先使用后定义,所以v仍被包含。因此针对上面公式更全面的理解:
那么仿照上节的reaching definition analysis可以写出algorithm of live variables analysis:

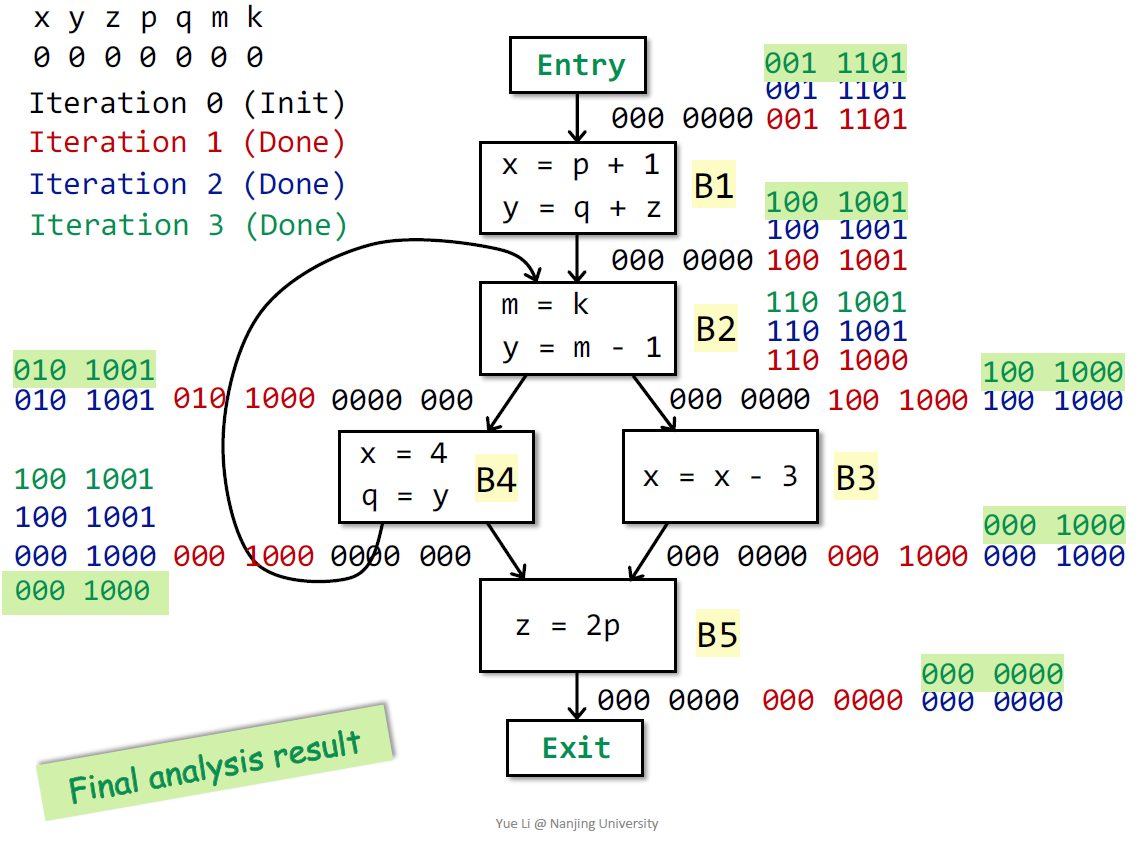
运行如下实例加深理解:
可用表达式分析

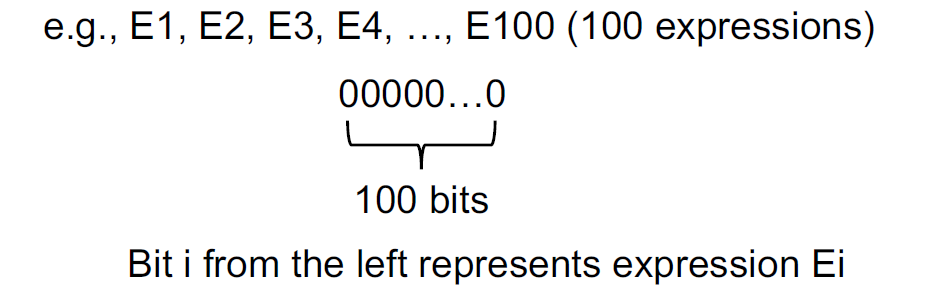
需要注意的关键点是,这属于must-approximation。同样采用位向量抽象表示:
进一步理解,这种分析针对的是表达式本身而不是表达式的值(静态分析):

公式与之前不同的点就在于Available Expressions Analysis是一种must-approximation,采用forwards的方式control flow应该采用交集。同样可以得到算法:

这里有一个值得注意的点就是对于basic block的初始化,这里初始化为U,也就是位向量中全1的形式,具体的理论原因在后续课程中会讲到。直观理解上,如果继续初始化为空集,那么在进行control flow的计算时,空集和其他集合的交集将会一直是空集。同样运行一个算法实例加深理解:
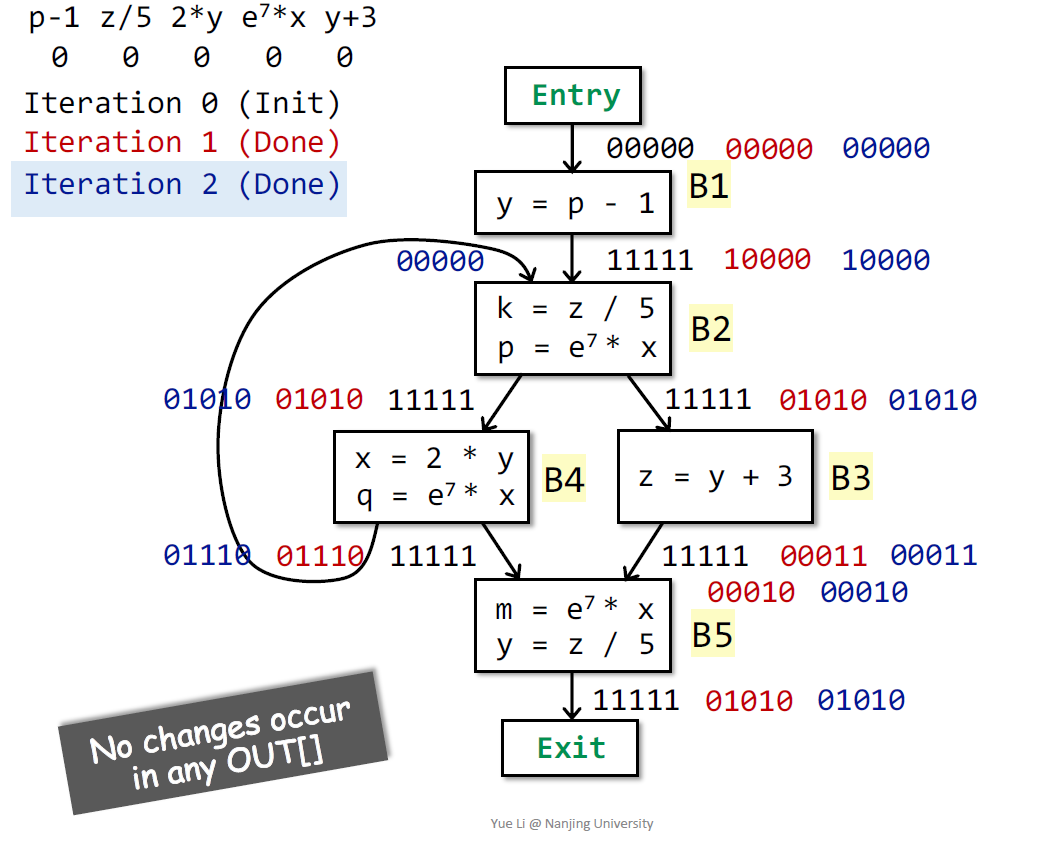
这里也有一点需要注意就是在B4中对于x的定义和对于e7x的使用。分析的方式是按照顺序,因为是先定义后使用,我们仍将e7x加入到位向量中(先kill后used)。
总结