NJU软件分析笔记(2)

NJU Static Analysis Notes(2)——Data Flow Analysis Ⅰ

课程链接
本次课程主要内容

Overview of Data Flow Analysis
Preliminaries of Data Flow Analysis
Reaching Definitions Analysis

数据流分析概览

和上节课的知识相连接，数据流分析在理解上就是数据在CFG上的流动过程分析，是一种抽象和over-approximation的方法。关于over-approximation（may analysis）和under-approximation（must analysis）在理解上就是，针对所有可能的错误（true），may analysis 给出的一定包含全部真正错误的，但可能有误报。但是must analysis给出的一定是所有错误中的一部分，不存在误报可能存在漏报。

在不同的情况下，可能需要may analysis或者 must analysis，因此采用safe-approximation的说法。

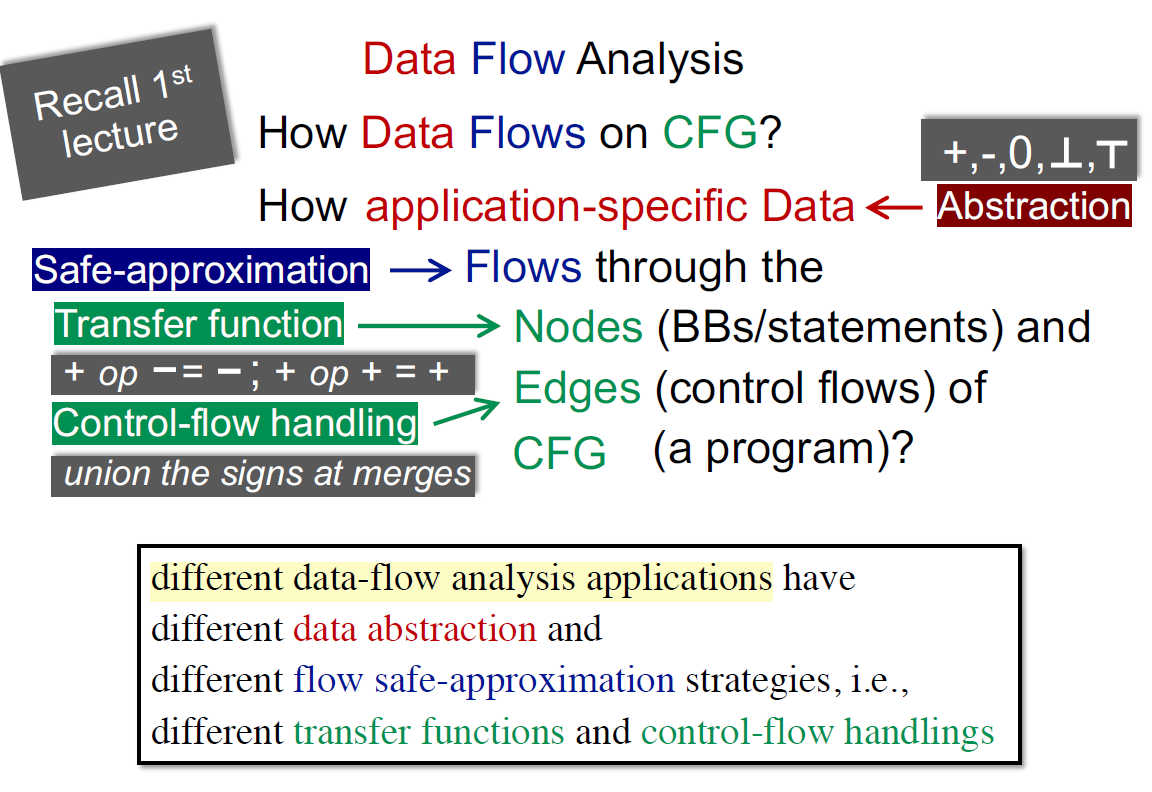
两个很重要的部分就是transfer function和control-flow handlings，因此后续对这部分进行一个形式化的研究。

DFA前置知识

每个IR语句的执行，会有一个IN state和一个OUT state，这两个状态和语句前后的program point相关联

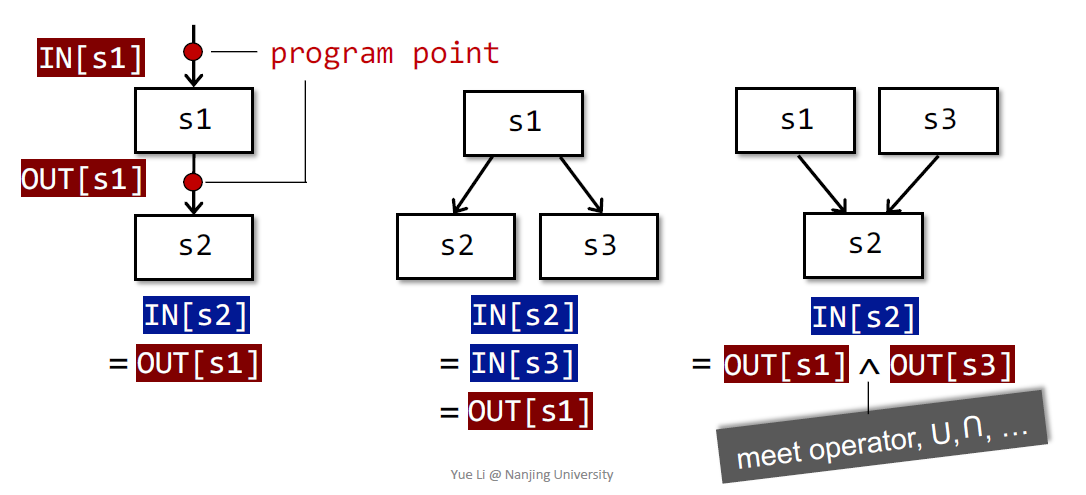
比如针对如下的IR，分析符号状态：

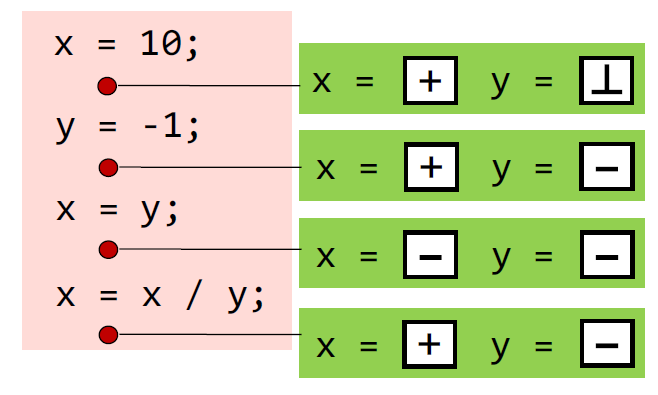
针对每一个program point 都会和一个data-flow value相关联上，这就是针对程序状态的一种抽象。那么数据流分析在形式上可以表述为

针对这段话的理解: 简单地说就是用一些约束作用在IN和OUT上得到程序的一个最终状态集合。（后续有例子）
形式化的定义需要先引入一些符号：

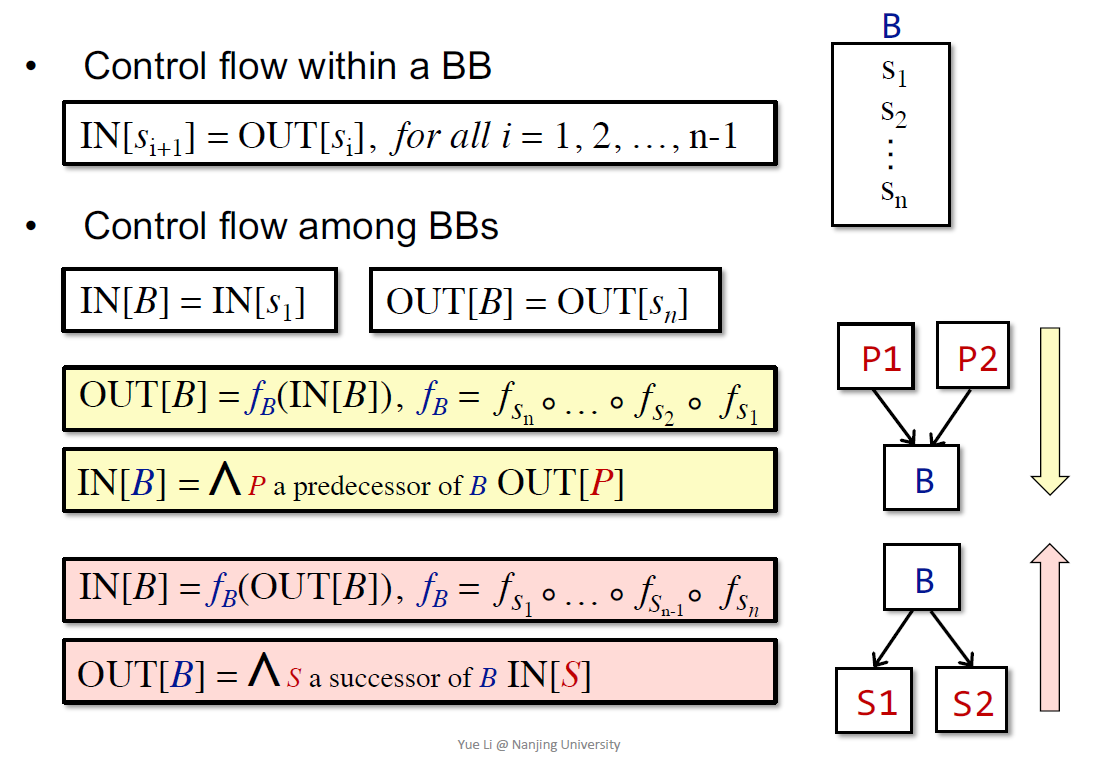
都是很自然的符号表示。
需要提前声明一下后续所处理的例子的特性，这两种情况不在本节讨论范围内：

可达定义（Reaching Definitions）分析

首先定义(definition)是针对一个变量来说的

那么这个定义是可以reach到另一个program point的定义如下

这里的不被kill掉，就是指，这条路径不会对该变量做另一次赋值。

可达定义分析可以用来检测可能的未定义行为：

下面介绍一些对于定义的符号，采用位向量的做法：

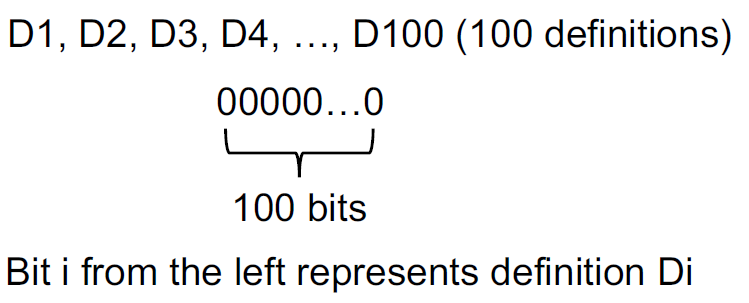
某一位置1表示该变量被定义。如果在某处出现了某变量的定义，那么其他关于该变量的定义被kill掉，如下的例子：

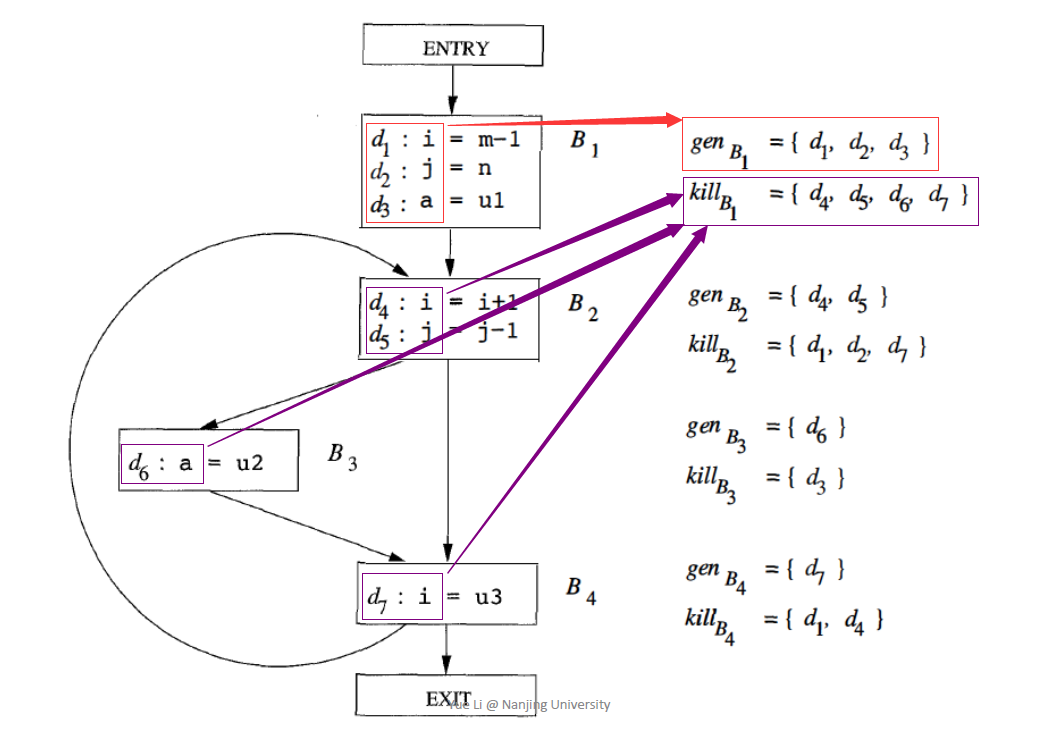
在B1中，d1,d2,d3定义了i,j,a，因此其他关于这三个变量的定义均为kill，所以在这一个Basic Block处，就定义：

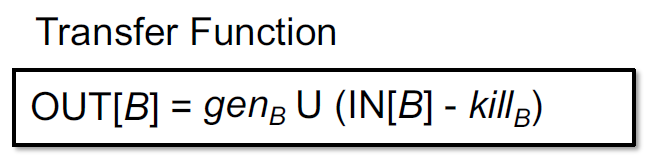
同样的IN可以定义如下：

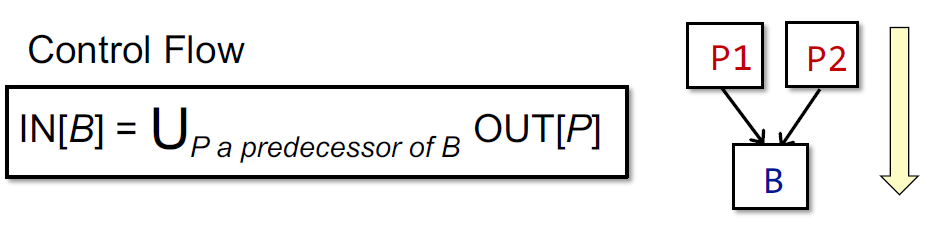
在有了上述的定义和符号以后，可以得到如下算法:

需要注意的是算法前三行的初始化，此处针对的是may-approximation,初始化为空是正确的。这段算法的解释可以是：只要有一个Basic Block的OUT在一轮迭代之后产生了变化，就针对所有的Basic Block运行前面提到的定义计算IN和OUT。针对如下的例子运行该算法

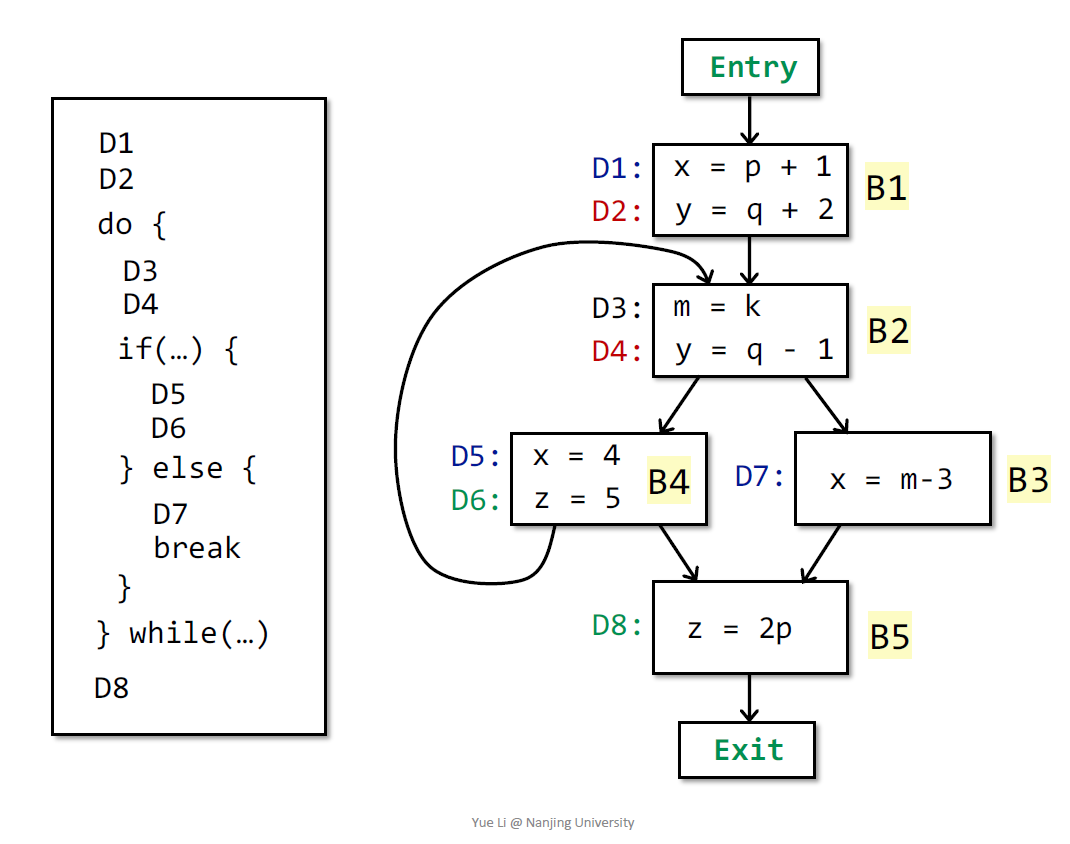
在经历三轮迭代之后程序得到了一个稳定的解：

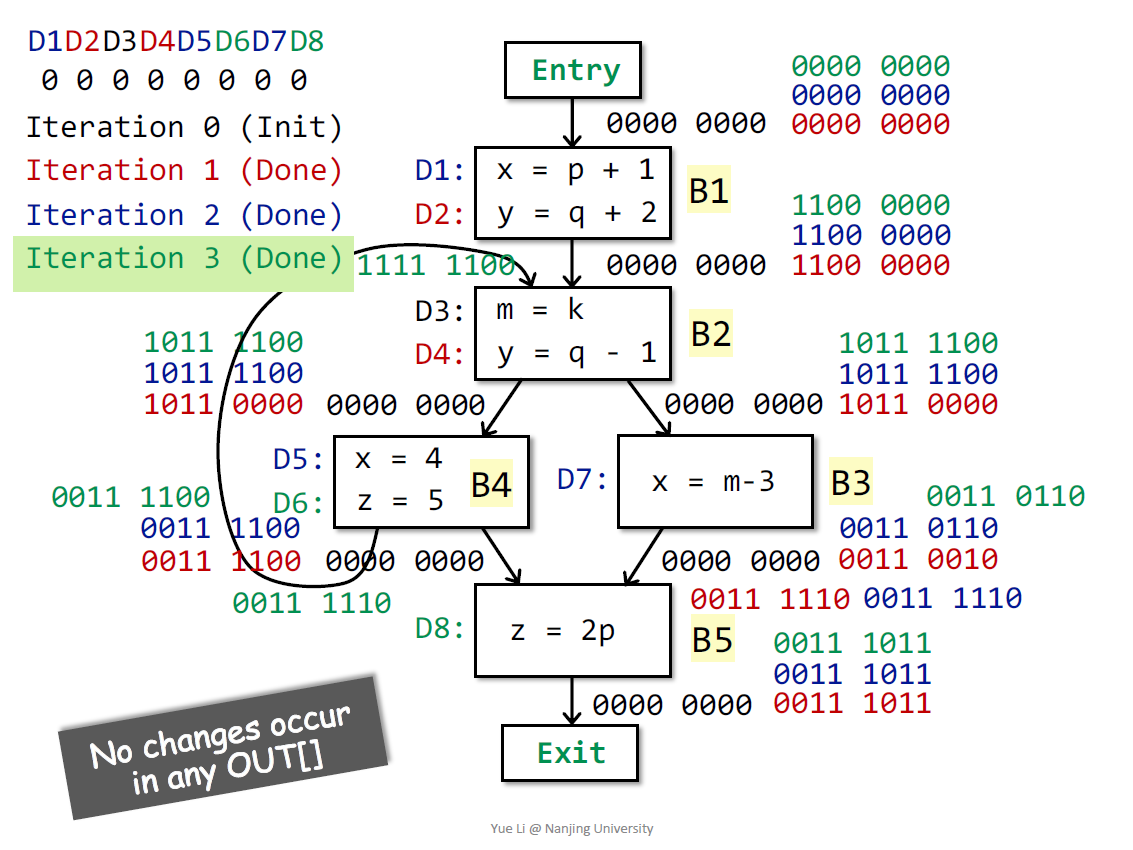
在这个例子上再回顾前面提到的这两段话：

另一个值得思考的是算法一定能停止吗？答案是肯定的：

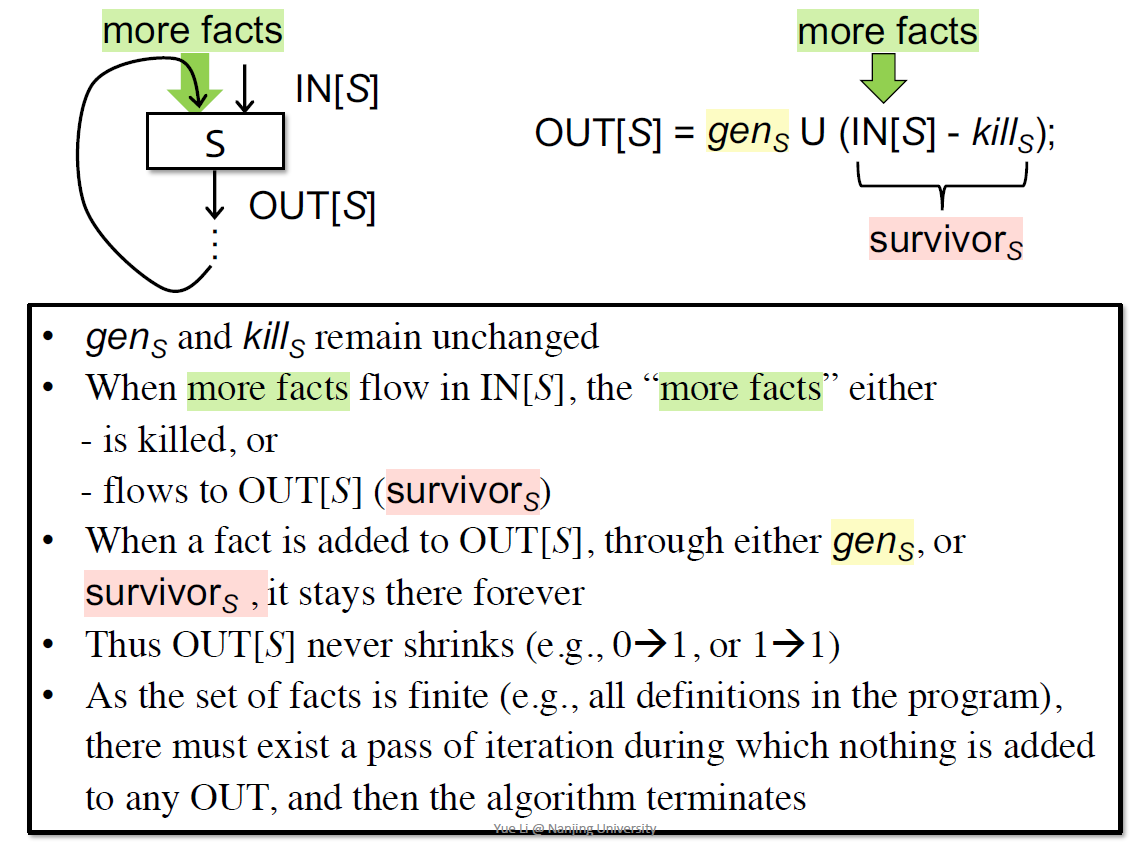
gen和kill针对每个block都是固定的，因此OUT只能是不变或者0变1，最终总会不变。