IEEE浮点数标准

IEEE浮点数标准

阅读笔记:Computer System : A Programmmer's Perspective

基本概念

IEEE浮点数标准采用

\[V=(-1)^s\times M\times2^E \]

的形式表示一个数：

• 符号：s决定数的正负

• 尾数：M是一个二进制小数，范围是1~2-epsilon 或者 0~1-epsilon

• 阶码：E的作用是对浮点数加权，权重为2的E次幂

下图为单精度(32位)与双精度(64位)的位示意图：

单精度：

• s：1位
• exp：k=8位
• frac：n=23位

双精度：

• s：1位
• exp：k=11位
• frac：n=52位

三个字段的编码：

1. 单独的s直接编码符号s

2. k位的阶码字段：

   \[exp=e_{k-1}e_{k-2}\cdots e_{1}e_{0} \]

编码E

3. n位的小数字段：
   \[frac=f_{n-1}f_{n-1}\cdots f_{1}f_{0} \]

编码M

编码的三种情况

规范化值

当exp的位即不全为0也不全为1时（即单精度范围：1~254 双精度范围：1~2046），即为规范化的值。这种情况下，阶码字段可以被解释为以偏置量（bias）形式表示的有符号整数

\[E=exp-bias \]

其中：exp即为阶码字段表示的值，并有

\[bias=2^{k-1}-1 \]

故对于单精度bias=127,双精度bias=1023,由此可得：

\[E=exp-127 \]

或者是：

\[E=exp-1023 \]

因此指数的范围：

\[E\in [-126,127] \]

或者是：

\[E\in [-1022,1023] \]

小数字段被解释为描述小数值f，0≤f<1,即：

\[f=\sum_{i=0}^{n-1}f_i*2^{i-n} \]

尾数定义为：

\[M=1+f \]

非规范化值

当阶码域全为0时，表示的数是非规范化的，此时的阶码为

\[E=1-bias \]

故E=-126(单精度)或者E=-1022(双精度)而尾数：

\[M=f \]

同理0≤f<1,即：

\[f=\sum_{i=0}^{n-1}f_i*2^{i-n} \]

用途：

• 表示数值0
• 表示非常接近0的数

特殊值

1. 无穷大

阶码全为1且小数字段全为0，根据符号位表示±∞

2. NaN

阶码全为1且小数字段不全为0，这不是一个数(Not a Number)

总结

值的表示：

\[V=(-1)^s\times M\times2^E \]

单精度：

1. 规范值:

   E=exp-bias

   bias=127

   M=1+f

2. 非规范：

   E=1-bias=-126

   bias=127

   M=f

双精度：

1. 规范值：

   E=exp-bias

   bias=1023

   M=1+f

2. 非规范值

   E=1-bias=-1022

   bias=1023

   M=f

示例

Q1.将-3.33333333转换为单精度表示

首先，将这个小数转化为二进制的小数形式(利用×2法)

\[-3.33333333_{10}=-11.010101010101..._{2} \]

规范化：

\[-3.33333333_{10}=-1.1010101010101..._{2}\times2^1 \]

因此：

\[s=1 \]

\[exp=E+bias=1+127=128_{10}=1000 0000_{2} \]

\[M=1.1010101010..._2\Rightarrow f=1010101010..._2 \]

从而可以写出单精度表示

\[11000000010101010101010101010101_2=C0555555_{16} \]

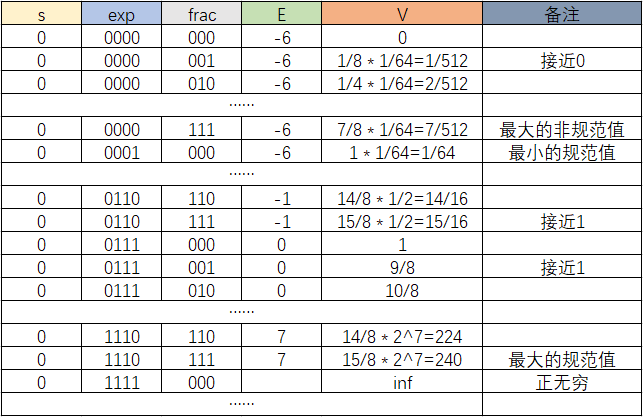
Q2.给出如图8位二进制数在IEEE标准的浮点格式

首先对于规范化值：

\[E=exp-bias=exp-7 \]

对于非规范值：

\[E=1-bias=-6 \]

可以写出如下表格：