可持久化线段————主席树(洛谷p3834)
洛谷P3834 可持久化线段树 2
问题描述:
- 给定n各整数构成的序列,求指定区间[L,R]内的第k小值(求升序排序后从左往右数第k个整数的数值)
输入:
- 第一行输入两个整数n,m,分别代表序列长度n和对序列的m次查询;
- 第二行输入n个整数,表示序列的n个整数;
- 之后的m行,每行输入3个整数L,R,k,表示查询[L,R]内的第k小值;
输出:
- 对于每个查询,输出查询区间内的第k小值;
数据范围:
- 1 ≤ n, m ≤ 2×
- 1 ≤ L≤ R ≤ n;
- 1 ≤ k ≤ R-L+1;
//第一次写mathjax,东找西找. 。·*༙ ✟ 升天 ✟ *༙· 。.
分析问题:
//以前学了点css总算用上了
题目这么直白,肯定是不能用暴力搜索先排序后定位总共m次查询算下来复杂度为O(mn
本题考虑使用线段树求解,但使用线段树求解问题的时候,需要满足大区间的解可以由小区间的解合并而来,也就是我们经常说的线段树叶子节点与根节点的关系,但是区间中第k小的问题似乎并不符合这一特征,总不能说得到左右两个孩子节点区间的第k小数(也就是两个小区间的解,就两个数),可以得出他们所组成的大区间的第k小数吧
但我们仔细想想,既然不能让第k小数成为每个区间的解,也就是利用线段树无法直接得到答案,我们或许可以换个角度入手,让两个线段树相减得到新的线段树,而新线段树对应了新区间的解
下面我们来逐步推出可持久化线段树的解题思路
-
既然是线段树相减,我们首先要搞清楚的是哪来的这么多线段树,这些线段树都想表达什么意思。先问个问题,该如何利用线段树求解第k小问题,比如给你一个区间[1,i],如何求第k小元素。
-
我们回顾下正常方法:先将区间内的所有元素排序,让后数个数,从左往右数第k个就是答案。这里可以数据化的有序列元素,元素个数,k,映射到线段树,编写线段树首先要弄清楚线段树区间解是什么,叶子节点代表什么。前面以经分析k无法成为线段树的区间解,显然序列元素也不行,那么试试元素个数,那么叶子节点代表排好序的序列。以序列{2,1,4,3}为例,如图:
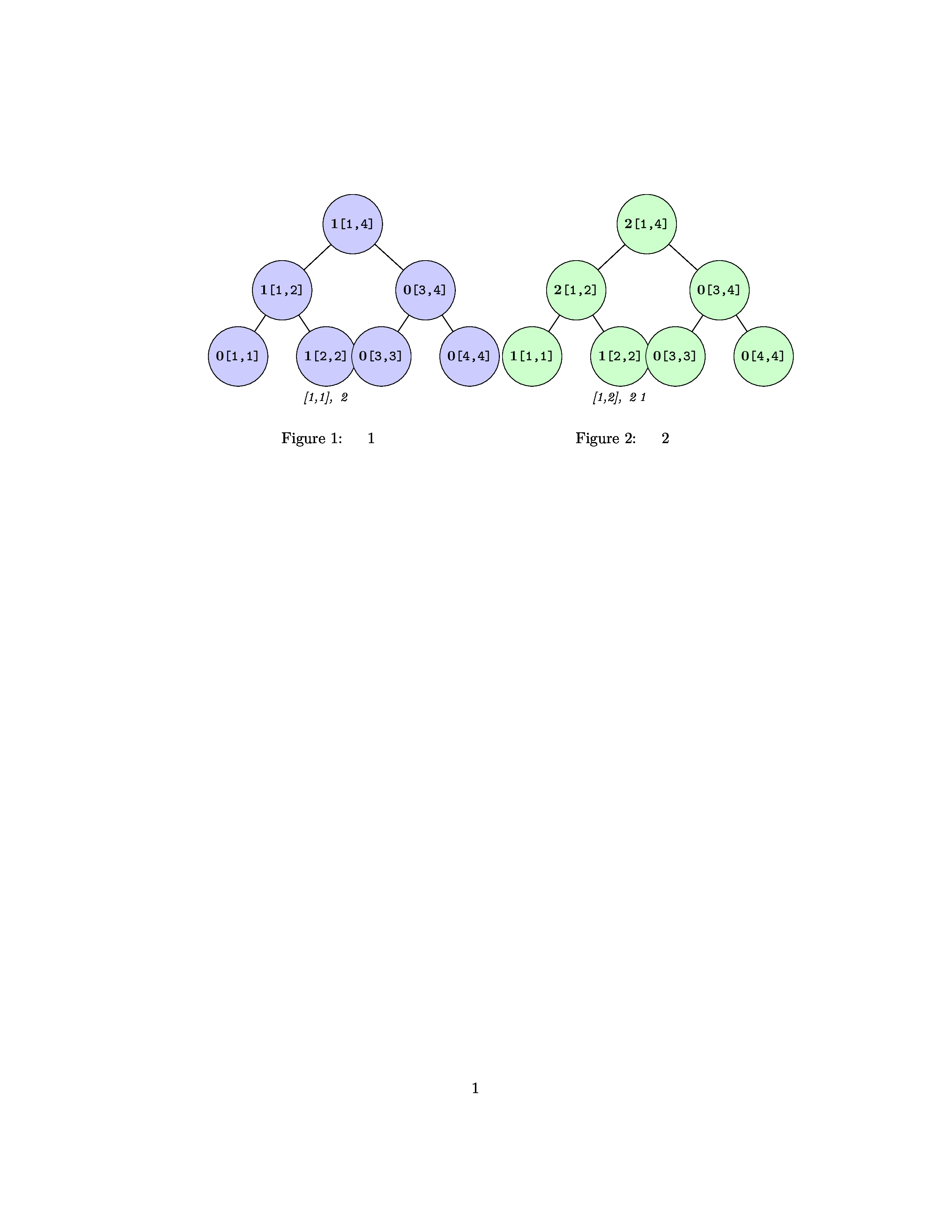
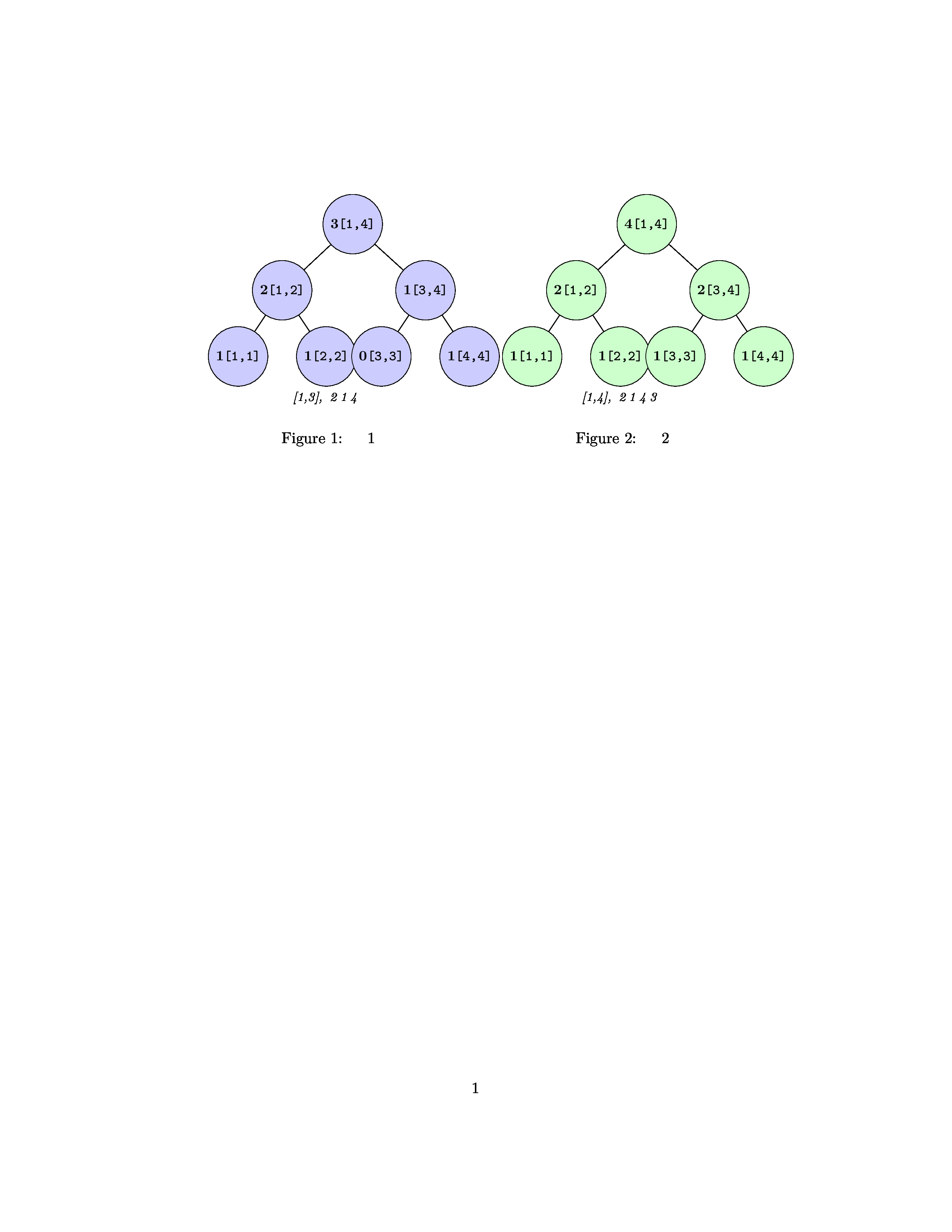
如需查找[1,3]内的第k小元素根节点3为区间内元素总数,当k=2时从根节点出发左孩子节点个数为2,由于叶子节点是有序的所以k≤2,则说明区间中第k小的树在左孩子节点;但如果第k小数在右孩子节点,当k=3时,k>2,此时k需要发生变化,不可能在右孩子节点上查找第3小的数(总共才一个数),数的左边已经有两个数了,查询必须在左边的基础上查,也就是在右边查找第k-2=1小的数,根据这个方法向下推直到叶子节点即可找到答案。
-
既然明白了求[1,i]区间第k小数问题的方法,那么如何求区间[L,R]内第k小数呢,有没有觉得这个问题很熟悉,对!就是前缀和思想,我们求[L,R]可以利用[1,L-1]区间的线段树-[1,R]区间的线段树,从而得到[L,R]区间的线段树,这在逻辑上是成立的,应为只是元素个数的相减,得出的答案任然是元素个数,然后利用求解[1,i]区间线段树第k小数的方法求解。
例如:求区间[2,4]的线段树,等于把第四个线段树与第一个线段树相减(对应圆圈中的数字相减)
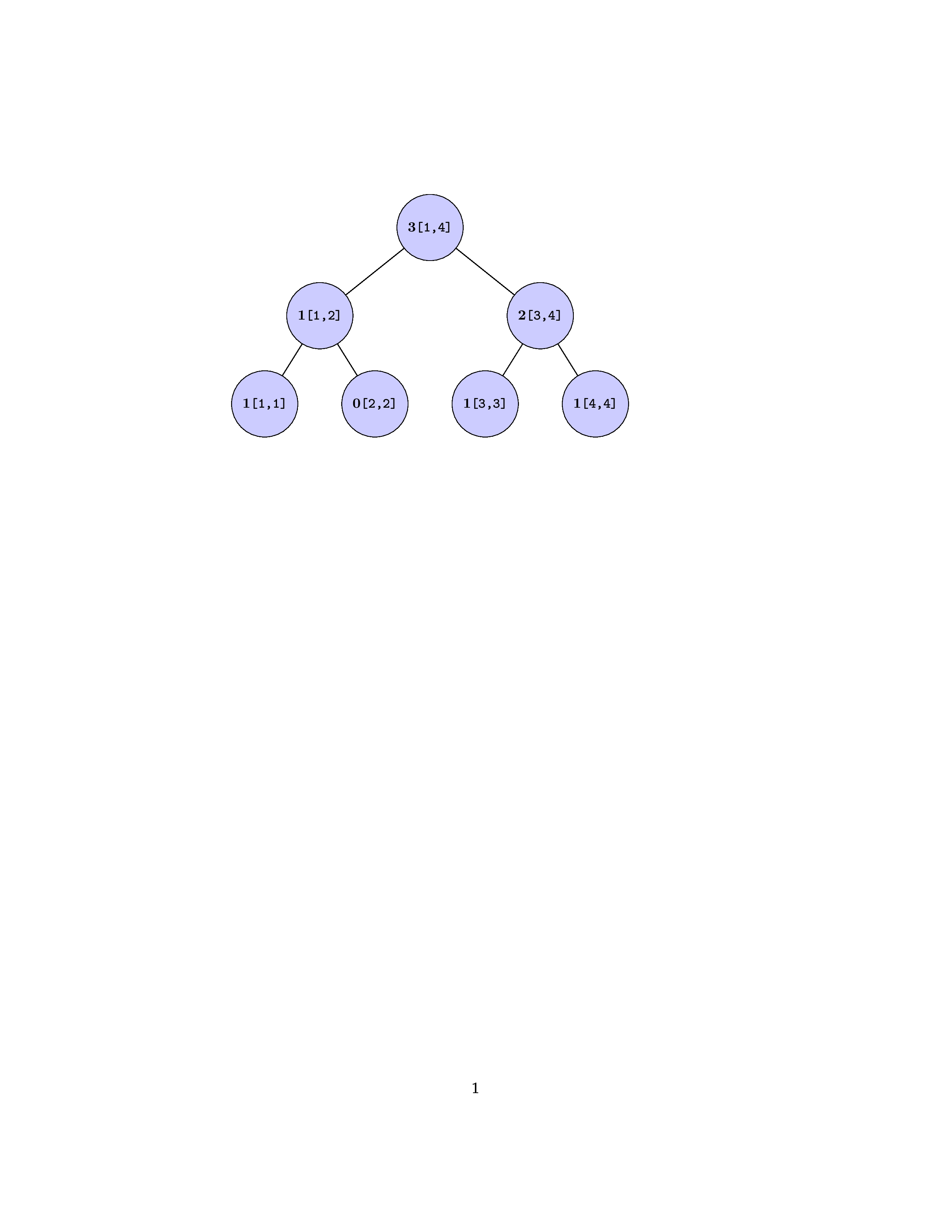
-
上点中的方法我们似乎要建立很多棵线段树,是的,这就是可持续化线段树,也就是常说的主席树。但这样就可以得到答案吗,前面说到将排序好的序列作为线段树的叶子节点而已知每个节点的值为当前节点及节点下孩子节点元素个数的总和,那么叶子节点的值不是0就是1,好像也不能作为答案,那么就只有区间可以作为答案,在叶子节点中pl=pr,而我们的例子中刚好pl=pr=答案,有同学肯定会说,你这是故意的,这个例子太特殊了。确实如果序列中的数不是连续的,比如{100,200,50,6000000},那么我每棵线段树叶子节点是不是要有6000000个,(只有四个叶子节点值为1)意味着总共4×6000000×2(×2的意思是加上了叶子节点上方的根节点,用等比数列算一算,差不多就是这个数)非常浪费空间。很容易想到利用离散化(求序列的第k小值与元素本身的大小其实并没有关系,只与元素之间的相对大小有关),将分布广而稀疏的数据转化为密集分布,从而使算法更快速更省空间地处理。
-
但使用离散化也有需要注意的要点————有关重复元素的处理。如序列{1,5,5,6,7},序列中第3小的元素不是6,而是5,说明重复元素也要计数,如何处理,摆在面前的有两个方法,1.在叶子节点上。2.在线段树建立个数上。我直接给答案了,第一种方法不行,在叶子节点上反正我是不知道这么做。序列中总共n个元素,建立n棵线段树[1,i],i从1到n。编码时对n个元素离散化,并用unique()函数去重得到size个不同的元素,每棵线段树中叶子节点的个数为size。其中重复的数字线段树结构不同,由于线段树每个节点的值为节点下孩子的个数,后面的5比前面的5路径上会多1(之后看代码理解,这个我不好表达)。
时间,空间的压榨
讲清楚思路之后,思考下如何编码才可以最大限度地压榨时间和空间
两棵树相减真的需要所有节点都相减吗,仔细观察[2,4]线段树得出的过程,会发现只需要对查询路径上的节点及左右区间做减法即可,简单说就是只需计算查询过程中使用节点即可,因为查询得到答案的过程也不是所有节点都会用上,一边更新一边查询(之后看代码你会理解)
真的需要建立n棵完整的线段树吗,和上面道理一样,既然查询过程中都用不上的节点为什么还要建立,但需要注意的是:查询区间不同,需要计算的节点也会不同。所以线段树我们改建还得建,但我们只建立一一棵完整的线段树,仔细观察上面建立的四棵线段树,会发现相邻线段树长得非常像,他们对应区间只相差一位数,其实线段树相差的那部分与这位数是有关系的,如果该位数从根节点出发到叶子节点会产生一台路径,会发现这条路径上的所有节点都与另一棵树上对应的节点相差1,所以我们完全可以只建立这条路径上的节点,剩下的节点与另一棵树共用,保证其逻辑上的完整性即可
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 20010;
int cnt = 0; //对根节点计数
int a[N], b[N], root[N]; //a存储原数组,b复制数组,root存储根节点
struct {
int L, R, sum; //sum记录该子树根节点下有几个元素
}tree[N<<5]; //为什么是N<<5,这个我是真不会
int build(int pl,int pr){
//该函数为建立初始线段树(可建可不建) 因为再建立有元素线段树的同时,之后的线段树结构会趋于完整,前面的线段树即使不完整也不影响其功能,因为不完整的部分不会被使用
int rt = cnt++; //每新增一个根节点,则需要增加计数,相当于为该线段树申请空间
tree[rt].sum = 0; //还未添加任何元素,所以所有根节点下元素个数都为零
//类似于dfs的算法
int mid = (pl + pr) >> 1;
if (pl < pr) {
//递归的同时开辟左右子树
tree[rt].L = build(pl, mid);
tree[rt].R = build(mid + 1, pr);
}
return rt; //返回下一位根节点的索引
}
int update(int pre,int pl,int pr,int x) {
//更新的同时也在建立各元素的线段树
int rt = ++cnt;
tree[rt].L = tree[pre].L; //将其与另一棵树的其他节点相连保证其逻辑上的完整性
tree[rt].R = tree[pre].R;
tree[rt].sum = tree[rt].sum + 1; //添加沿路节点
//有点像二分查找
int mid = (pl + pr) >> 1;
if (pl < pr) {
if (x < mid) {
update(tree[pre].L, pl, mid, x);
}
else {
update(tree[pre].R, mid + 1, pr, x);
}
}
return rt; //返回建立的该线段树的根节点
}
int query(int u, int v, int pl, int pr, int k) {
//返回搜索结果的索引,注意这里是b数组的索引
//这里没有使用cnt变量,实际上并没有建立[L,R]区间的线段上,我们的目的只是为了找到一条路径指向第k小数即可
if (pl == pr) return pl;
int x = tree[tree[v].L].sum - tree[tree[u].L].sum;
int mid = (pl + pr) >> 1;
if (x >=k){
return query(tree[u].L, tree[v].L, pl, mid, k);
}
else {
//注意这里是k-x
return query(tree[u].R, tree[v].L, mid + 1, pr, k-x);
}
}
int main() {
int n, m; cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = a[i];
}
sort(b + 1, b + 1 + n);
//离散化标准操作
int size = unique(b + 1, b + 1 + n) - b - 1;
root[0] = build(1, size); //一棵树的尺寸是size,数组中不相同数字的个数
for (int i = 1; i <= n; i++) {
//建立n棵树
//注意这里是-b
int x = lower_bound(b + 1, b + 1 + n,a[i]) - b;
root[i] = update(root[i - 1], 1, size, x);
}
while (m--) {
int x, y, k; cin >> x >> y >> k;
int t = query(root[x - 1], root[y], 1, size, k);
//别忘了把索引的值打印出来
cout << b[t] << endl;
}
return 0;
}
第一篇博客,标记一下***



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】