位运算处理N皇后

n皇后问题位运算版
    n皇后问题是啥我就不说了吧，学编程的肯定都见过。下面的十多行代码是n皇后问题的一个高效位运算程序，

看到过的人都夸它牛。初始时，upperlim:=(1 shl n)-1。主程序调用test(0,0,0)后sum的值就是n皇后总的解数。

procedure test(row,ld,rd:longint);
var
      pos,p:longint;
begin

{ 1}  if row<>upperlim then
{ 2}  begin
{ 3}     pos:=upperlim and not (row or ld or rd);
{ 4}     while pos<>0 do
{ 5}     begin
{ 6}        p:=pos and -pos;
{ 7}        pos:=pos-p;
{ 8}        test(row+p,(ld+p)shl 1,(rd+p)shr 1);
{ 9}     end;
{10}  end
{11}  else inc(sum);

end;
    乍一看似乎完全摸不着头脑，实际上整个程序是非常容易理解的。这里还是建议大家自己单步运行一探究竟，实在没研究出来再看下面的解说。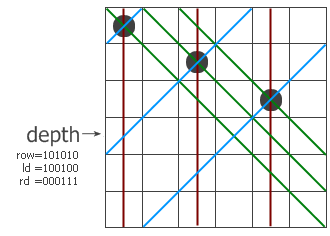

  
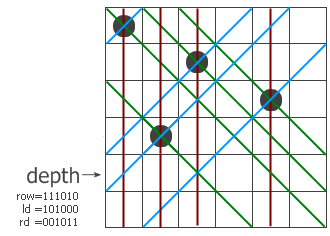
    和普通算法一样，这是一个递归过程，程序一行一行地寻找可以放皇后的地方。过程带三个参数，row、ld和rd，

分别表示在纵列和两个对角线方向的限制条件下这一行的哪些地方不能放。我们以6x6的棋盘为例，看看程序是怎么工作的。

假设现在已经递归到第四层，前三层放的子已经标在左图上了。红色、蓝色和绿色的线分别表示三个方向上有冲突的位置，

位于该行上的冲突位置就用row、ld和rd中的1来表示。把它们三个并起来，得到该行所有的禁位，

取反后就得到所有可以放的位置（用pos来表示）。

前面说过-a相当于not a + 1，这里的代码第6行就相当于pos and (not pos + 1)，其结果是取出最右边的那个1。

这样，p就表示该行的某个可以放子的位置，把它从pos中移除并递归调用test过程。注意递归调用时三个参数的变化，

每个参数都加上了一个禁位，但两个对角线方向的禁位对下一行的影响需要平移一位。最后，

如果递归到某个时候发现row=111111了，说明六个皇后全放进去了，此时程序从第1行跳到第11行，找到的解的个数加一。

根据上面的理论，可以解决下面的这道题目。

Description

Examine the 6x6 checkerboard below and note that the six checkers are arranged on the board so that one and only one is placed in each row and each column, and there is never more than one in any diagonal. (Diagonals run from southeast to northwest and southwest to northeast and include all diagonals, not just the major two.)

          Column
    1   2   3   4   5   6
  -------------------------
1 |   | O |   |   |   |   |
  -------------------------
2 |   |   |   | O |   |   |
  -------------------------
3 |   |   |   |   |   | O |
  -------------------------
4 | O |   |   |   |   |   |
  -------------------------
5 |   |   | O |   |   |   |
  -------------------------
6 |   |   |   |   | O |   |
  -------------------------

The solution shown above is described by the sequence 2 4 6 1 3 5, which gives the column positions of the checkers for each row from 1 to 6:

 

ROW	1	2	3	4	5	6
COLUMN	2	4	6	1	3	5

This is one solution to the checker challenge. Write a program that finds all unique solution sequences to the Checker Challenge (with ever growing values of N). Print the solutions using the column notation described above. Print the the first three solutions in numerical order, as if the checker positions form the digits of a large number, and then a line with the total number of solutions.

Special note: the larger values of N require your program to be especially efficient. Do not precalculate the value and print it (or even find a formula for it); that's cheating. Work on your program until it can solve the problem properly.

 

Input

A single line that contains a single integer N (6 <= N <= 13) that is the dimension of the N x N checkerboard.

Output

The first three lines show the first three solutions found, presented as N numbers with a single space between them. The fourth line shows the total number of solutions found.

Sample Input

6

Sample Output

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

#include<iostream>
using namespace std;
#define Max 14
int Row[Max], n, numofsolve; 
void SolveWithBit(int p, int row, int lb, int rb)
{
	if(p>n) //找到了解
	{
		numofsolve++;
		if(numofsolve <=3) //判断解的个数 
		{
			for(int i=1; i<n; i++)
				cout<<Row[i]<<" ";
			cout<<Row[n]<<endl;
		}
	}

	for(int i=1; i<=n; i++)
	{
		int t = (1<<(i-1)); //用t来试探可用位置
		if((t & (row | lb | rb))==0) //(row | lb | rb)表示本行中所有禁用的位置，t就是表示本行中所有的可用位
		{
			Row[p] = i; //i位可用
			SolveWithBit(p+1, row|t, (lb|t)<<1, (rb|t)>>1);
		}
	}
}
int main()
{
	cin>>n;
	int re;
	for(int i=1; i<=n; i++)
	{
		Row[1] = i; //初始化第一行，有n个状态
		SolveWithBit(2, 1<<(i-1), 1<<i, 1<<(i-2)); //从第二行开始搜索		
	}
	cout<<numofsolve<<endl;
}