Floyd算法解决POJ 1603
Description
Risk is a board game in which several opposing players attempt to conquer the world. The gameboard consists of a world map broken up into hypothetical countries. During a player's turn, armies stationed in one country are only allowed to attack only countries with which they share a common border. Upon conquest of that country, the armies may move into the newly conquered country.
During the course of play, a player often engages in a sequence of conquests with the goal of transferring a large mass of armies from some starting country to a destination country. Typically, one chooses the intervening countries so as to minimize the total number of countries that need to be conquered. Given a description of the gameboard with 20 countries each with between 1 and 19 connections to other countries, your task is to write a function that takes a starting country and a destination country and computes the minimum number of countries that must be conquered to reach the destination. You do not need to output the sequence of countries, just the number of countries to be conquered including the destination. For example, if starting and destination countries are neighbors, then your program should return one.
The following connection diagram illustrates the first sample input.
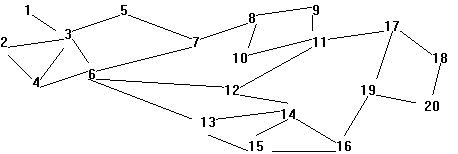
During the course of play, a player often engages in a sequence of conquests with the goal of transferring a large mass of armies from some starting country to a destination country. Typically, one chooses the intervening countries so as to minimize the total number of countries that need to be conquered. Given a description of the gameboard with 20 countries each with between 1 and 19 connections to other countries, your task is to write a function that takes a starting country and a destination country and computes the minimum number of countries that must be conquered to reach the destination. You do not need to output the sequence of countries, just the number of countries to be conquered including the destination. For example, if starting and destination countries are neighbors, then your program should return one.
The following connection diagram illustrates the first sample input.

Input
Input to your program will consist of a series of country configuration test sets. Each test set will consist of a board description on lines 1 through 19. The representation avoids listing every national boundary twice by only listing the fact that country I borders country J when I < J. Thus, the Ith line, where I is less than 20, contains an integer X indicating how many "higher-numbered" countries share borders with country I, then X distinct integers J greater than I and not exceeding 20, each describing a boundary between countries I and J. Line 20 of the test set contains a single integer (1 <= N <= 100) indicating the number of country pairs that follow. The next N lines each contain exactly two integers (1 <= A,B <= 20; A!=B) indicating the starting and ending countries for a possible conquest.
There can be multiple test sets in the input file; your program should continue reading and processing until reaching the end of file. There will be at least one path between any two given countries in every country configuration.
There can be multiple test sets in the input file; your program should continue reading and processing until reaching the end of file. There will be at least one path between any two given countries in every country configuration.
Output
For each input set, your program should print the following message "Test Set #T" where T is the number of the test set starting with 1. The next NT lines each will contain the result for the corresponding test in the test set - that is, the minimum number of countries to conquer. The test result line should contain the start country code A the string " to " the destination country code B ; the string ": " and a single integer indicating the minimum number of moves required to traverse from country A to country B in the test set. Following all result lines of each input set, your program should print a single blank line.
Sample Input
1 3
2 3 4
3 4 5 6
1 6
1 7
2 12 13
1 8
2 9 10
1 11
1 11
2 12 17
1 14
2 14 15
2 15 16
1 16
1 19
2 18 19
1 20
1 20
5
1 20
2 9
19 5
18 19
16 20
Sample Output
Test Set #1
1 to 20: 7
2 to 9: 5
19 to 5: 6
18 to 19: 2
16 to 20: 2
说句实话,这个输入真的有点蛋庝呀!
还好题目十分的简单。
你要想学好floyd,不妨先去看看松驰操作。
懂了松驰操作,floyd不在话下。而且松驰
操作在其它的算法中也是十分的常用。所以
弄懂这个十分有必要。
 View Code
View Code
#include "iostream" using namespace std; #define Max 21 int map[Max][Max]; void floyd() { for(int m=1; m<=20; m++)//m代表mid,即中间的点 for(int b=1; b<=20; b++)//b代表begin,即开始的点 for(int e=1; e<=20; e++)//e代表end,即结束的点 if(map[b][e]>map[b][m]+map[m][e]) map[b][e] = map[b][m]+map[m][e]; } int main() { int n, num, end, i, j, start, count=1; while(cin>>num) { memset(map, 21, sizeof(map));//这个松驰操作关键的第一步,也是关键的一步 while(num--) { cin>>end; map[1][end]=map[end][1]=1;//初始化map,注意初始时的双向性 } for(i=2; i<=19; i++) { cin>>num; while(num--) { cin>>end; map[i][end]=map[end][i]=1;//初始化map,注意初始时的双向性 } } floyd(); cin>>n; cout<<"Test Set #"<<count++<<endl; while(n--) { cin>>start>>end; cout<<start<<" to "<<end<<": "<<map[start][end]<<endl; } cout<<endl; } return 0; }
posted on 2011-10-03 19:42 More study needed. 阅读(542) 评论(0) 编辑 收藏 举报






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 地球OL攻略 —— 某应届生求职总结
· 提示词工程——AI应用必不可少的技术
· Open-Sora 2.0 重磅开源!
· 周边上新:园子的第一款马克杯温暖上架