算法

填空

1.程序的概念

程序是一组计算机能识别和执行的指令，运行于电子计算机上，满足人们某种需求的信息化工具。

计算机的本质是程序的机器，程序是计算机的灵魂、算法是程序的灵魂

计算机程序 = 算法 +数据结构

2.算法的三要素

操作、控制结构与数据结构

3.结构化程序设计的要点

1）自顶向下，逐步求精

2）模块化设计

3）结构化编码

4.评价一个算法的复杂度

时间复杂度

计算机资源，最重要的是时间资源与空间资源。因此，算法的复杂性有时间复杂性与空间复杂性之分。需要计算机时间资源的量称为时间复杂度，需要计算机空间资源的量称为空间复杂度。时间复杂度与空间复杂度集中反映算法的效率。

5.最优子结构特性以及最优性原理的概念

最优性原理

作为整个过程的最优策略具有这样的性质，无论过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略

最优子结构特性

当一个问题的最优解中包含了子问题的最优解时，则称该问题具有最优子结构特性。

问题的最优解包含子问题的最优解，即后面阶段的状态可以通过前面阶段的状态推导出来

6.递推算法的概念以及步骤、递推关系式

递推算法的基本思想

把一个复杂的庞大的计算过程转化为简单过程的多次重复，该算法充分利用了计算机的运算速度快和重复操作的特点，从头开始一步步地推出问题最终的结果

实施递推的步骤

1）确定递推的变量

2）确定递推关系

3）确定初始（边界）条件

4）递推过程的控制

递推关系式

是解决问题的关键

7.牛顿迭代关系式

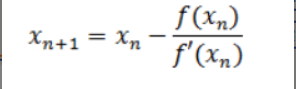
8.组合数的计算迭代公式

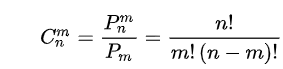
9.贪心算法的概念、思想、原理

概念

贪心法又被称为贪婪算法，从某一起点开始，就是在每一个解决问题步骤中使用贪心原则，即采取当前状态下最有利或最优化的选择，不断地改进该解答，持续在每一步骤中选择最佳的方法，并且逐步逼近给定的目标，当达到某一步骤不能再继续前进时算法停止，以尽可能快地求得更好地解。

思想

贪心算法是在当前情况下做出的最优决定，它只考虑眼前，获得的是局部的最优解，并且，希望通过每次获得局部最优解最后找到全局的最优解。具有最优子结构性质和贪心选择性质（可行的，局部最优，不可取消）。

贪心算法的基本步骤为

步骤1：从某一起点出发。 步骤2：在每一个解决问题步骤中，根据局部最优策略，得到一部分解，缩小问题规模。 步骤3：将所有解综合起来。

10.动态规划算法的基本思想、概念

动态规划过程是：每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

由于动态规划解决的问题多数有重叠子问题这个特点，为减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。

11.给两个序列，找出两个序列最长公共子序列

12.广度优先，最小耗费的方式搜索问题解的算法是什么算法

分支限界法（基本思想）：是一种在问题的解空间树(子集/排列树)上搜索问题解的算法.该算法只找出满足约束条件的一个最优解,并且以广度优先或最小耗费优先（最大效益）的方式搜索解空间树。 在搜索时，每个结点只有一次机会成为扩展结点,并且一次性产生其所有儿子结点。

13.二分搜索算法实例用什么实现

14.常用的时间复杂度的排序

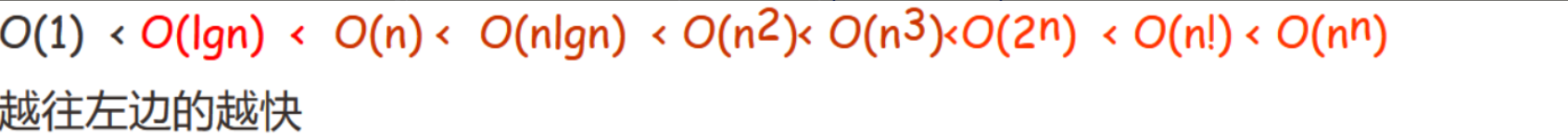
15.模拟算法的名字、思想、小名

16.什么叫哈夫曼树，给一个序列，摆一个哈夫曼树

17.汉诺塔的递归方程、公式理解

n个圆盘从A桩全部移到C桩上的移动次数:

g(n)=2*g(n-1)+1 g(1)=1

18.分支限界法的两种方法

队列式分支限界法

按照队列先进先出原则，选取下一个节点为扩展结点。

搜索策略

1. 一开始,根结点是唯一的活结点,根结点入队。

2. 然后，从活结点队中取出根结点后，作为当前扩展结点。

3. 对当前扩展结点，先从左到右地产生它的所有儿子，并用约束条件检查，把所有满足约束函数的儿子加入活结点队列中

4. 再从活结点表中取出队首结点（队中最先进来的结点）为当前扩展结点，…，直到找到一个解或活结点队列为空为止

优先队列式分支限界法

为了加速搜索的进程,按照优先队列中规定的优先级，选取优先级最高的结点,成为当前扩展结点。

搜索策略

1. 首先，对每一活结点,计算一个优先级（某些信息的函数值

2. 然后，根据这些优先级,从当前活结点表中优先选择一个优先级最高（最有利）的结点作为扩展结点,使搜索朝着解空间树上有最优解的分支推进,以便尽快地找出一个最优解

3. 再从活结点表中，取下一个优先级别最高的结点为当前扩展结点，…，直到找到一个解或活结点队列为空为止

 

选择

1.关于台湾收复的问题

2.算法复杂度排序的正确性

3.递归算法的步骤、概念、思想原理

基本步骤

构建递归关系、确定递归边界、写出递归函数、设计主函数调用递归函数

基本要素

边界条件、递归函数

思想原理

用与自身问题想似但规模较小的问题来描述自己。

通过函数或过程调用自身将问题转化为本质相同但规模较小的子问题。

递归算法概念

递归做为一种算法在程序设计语言中广泛应用.是函数/过程/子程序在运行过程序中直接或间接调用自身而产生的重入现像.

程序调用自身的编程技巧称为递归（ recursion）。 一个过程或函数在其定义或说明中又直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。用递归思想写出的程序往往十分简洁易懂。 一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

注意：

(1) 递归就是在过程或函数里调用自身; (2) 在使用递增归策略时，必须有一个明确的递归结束条件，称为递归出口，否则将无限进行下去（死锁）。

递归算法一般用于解决三类问题：

(1)数据的定义是按递归定义的。(Fibonacci函数) (2)问题解法按递归算法实现。(回溯)) (3)数据的结构形式是按递归定义的。(树的遍历，图的搜索)

递归的缺点：

递归算法解题的运行效率较低。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。

4.算法行数越少，复杂度越低

× 算法的执行频数的数量级直接决定算法的时间复杂度

5.可拆分的背包问题，给一组数，算获得的最大利润，徒手消灭简单的可拆分背包问题

贪心选择 算权重

操作时首先把各物品按单位重量的效益进行降序排列，从单位重量效益高的物品开始，一件件物品装包。直至受重量约束某一件物品装不下时，则装该物品的一部分把包装满。

6.什么叫二维背包问题

0-1背包问题 - alex.shu - 博客园 (cnblogs.com)

7.算法调试程序可以证明算法的正确性吗

8.递归算法与递推算法的复杂度谁高

• 递归是从问题的最终目标出发，逐渐将复杂问题化为简单问题，最终求得问题是逆向的。

• 递推是从简单问题出发，一步步的向前发展，最终求得问题，是正向的。

• 递归表现为自己调用自己，递推则没有这样的形式。·

• 一般来说，递推的效率高于递归,因此将递归转化为递推。

9.泊松分酒问题

10.蒙特卡罗算法的理解

蒙特卡洛算法是一种以概率和统计理论方法为基础的一种随即模拟方法，可使用随机数（或更常见的伪随机数）来求解很多计算机问题的近似解。

11.集装箱装载问题是否有解、判断的规则、公式

装载问题转化为一艘船的装载：设所有货物的重量之和为s，两艘船的载重量c1，c2，若载重量为c1的船所载的实际重量s1满足条件：s-c2<=s1<=c1 即 s-s1<=c2

可知两船可顺利完成装载。

12.单元最短路径问题 （迪杰斯特拉是什么算法）

迪杰斯特拉算法（求最短路径） (biancheng.net)

13.动态规划算法的步骤

1. 把所求最优化问题分成若干个阶段，找出最优解的性质，并刻划其结构特性

2. 将问题发展到各个阶段时所处不同的状态表示出来，确定各个阶段状态之间的递推（或递归）关系，并确定初始（边界）条件。

3. 应用递推（或递归）求解最优值。

4. 根据计算最优值时所得到的信息，构造最优解。

14.分支限界法的搜索是以什么方式搜索空间树的

基本步骤

1. 按广度优先的原则进行搜索，每一活结点只有一次机会成为扩展结点。

2. 活结点一旦成为扩展结点，就一次性产生其所有儿子结点。

3. 在这些儿子结点中:

• 导致不可行解的儿子结点，被舍弃

• 其余儿子结点，加入活结点表中

此后，从活结点表中取下一结点成为当前扩展结点,并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

15.关于算法说法的正确性（概念）

算法：一步步正确解决问题的方法与策略

算法是由若干条指令组成的有序序列，规定了某一个特定类型问题的一系列运算步骤

确定性：组成算法的每条指令是清晰的、无歧义的

16.使用回溯法进行状态空间树裁剪分割一般有两个标准 哪一种算法用约束条件，哪一种算法用约束函数

可行性约束函数

• 剪去不满足约束条件的子树。

上界函数

• 剪去不含最优解的子树,改进算法效率。

17.以深度优先方式系统搜索问题的算法有什么

回溯法（具有剪枝函数的深度优先生成法称为回溯法）

回溯法是一种选优搜索法,按选优条件向前搜索，以达到目标。但是，当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术，称为回溯法。

原理 回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否 包含问题的解:若肯定不包含问题的解,则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯；否则，进入该子树,继续按深度优先策略搜索。

18.贪心算法的两个重要性质

• 贪心选择性质（最优量度标准）

  我们可以做出局部最优选择来构造最优解。也就是说，我们在做出选择时，总是以当前的情况为基础做出最优选择的，而不用考虑子问题的解！

• 最优子结构性质

  如果一个问题的最优解包含其子问题的最优解，那么就称这个问题具有最优子结构性质！

程序填空

1.Pell方程

Pell方程是关于整数x,y的二次不定方程，表述为x^2-ny^2=1

通常把x,y中有一个为0的解称为平凡解，通常需求Pell方程的非平凡解

#include<stdio.h>
#include<math.h>
int main(){
    double x,y,n,a,m;
    printf("解PELL方程：x^2-ny^2=1 \n");
    printf("请输入非平方整数 n：");
    scanf("%lf",&n);
    m=floor(sqrt(n+1));
    if(m*m == n){
        printf("n是为平方数，方程无正整数解！\n");
        return 0;
    }
    y=1;
    while(y<10000000){
        y++;
        a=y*y*n;
        x=floor(sqrt(a+1));
        if(x*x == a+1){
            printf("方程x^2-%.0fy^2=1的基本解为：\n",n);
            printf("x=%.0f,y=%.0f\n",x,y);
            break;
        }
    }
    if(y>10000000)
      printf("未求出该方程的基本解！"); 
}

2.求代数和

//求代数和  s = 1 + 1/2 - 1/3 + 1/4 + 1/5 - 1/6 + ...+- 1/n
#include <stdio.h>
int main(){
    long n,k;
    double s = 0;
    printf("请输入正整数 n:");
    scanf("%ld",&n);
    for(k = 1;k <= n;k++)
    {
        if(k % 3 >0)
          s = s + 1.0/k;
        else 
          s = s - 1.0/k;
    }
    printf("s(%ld)=%.6f\n",n,s);
    return 0;
}

3.给出一个整数，删除K个数后，要么最大要么最小

 

#include <stdio.h>
int main(){
    int i,j,k,m,n,x,a[100];         //n:多少整数位  x:删除数字个数  k:要删除数字个数 
    char b[100];
    printf("请输入整数：");
    scanf("%s",b);       //以字符串的方式输入高进度整数
    for(n=0,i=0;b[i]!='\0';i++)
      {
        n++;
        a[i]=b[i]-48;
       } 
    printf("删除数字个数：");
    scanf("%d",&k);
    printf("以上%d位整数中删除%d个数字分别为：",n,k);
    i=0;
    m=0;
    x=0;
    while(k>x && m==0)
    {
        i=i+1;
        if(a[i-1]>a[i]){               //出现递减，删除左边的数字 
            printf("%d、",a[i-1]);
            for(j=i-1;j<=n-x-2;j++)      //删除数字后，后面的数字往前移   
            a[j]=a[j+1];
            x= x+1;
            i=0;          
        }
        if(i==n-x-1)
        m=1;                      //已无递减区间，m=1脱离循环 
     } 
     printf("\n删除后所得最小数：");
     for(i=1;i<=n-k;i++)
       printf("%d",a[i-1]);
     printf("\n");
     return 0; 
} 
​

 

定义一个数列，把数列的n项之和求出来

递推求解

#include <stdio.h>
int main(){
    int k,n;
    long b[3000],s;
    printf("请输入n：");
    scanf("%d",&n);
    b[1]=1;
    b[2]=2;
    s=3;
    for(k=3;k<=n;k++)
    {
        b[k]=3*b[k-1]-b[k-2];
        s+=b[k];
     } 
     printf("b(%d)=%ld\n",n,b[n]);
     printf("s=%ld",s);
     return 0;
} 

递归求解

 

#include <stdio.h>
long b(int n){
    long g;
    if(n==1) 
      g=1;
    else if(n==2)
      g=2;
    else 
      g=3*b(n-1)-2*b(n-2);
    return (g);  
}
int main (){
    int k,n;
    long s=0;
    printf("请输入n:");
    scanf("%d",&n);
    for(k=1;k<=n;k++)
      s+=b(k);
    printf("b(%d)=%ld\n",n,b(n));
    printf("s=%ld",s);
    return 0;
}

车站进站模拟、大概多少时间

#include <stdio.h> 
#include <time.h>
#include <stdlib.h> 
int main(){
    int i,n,m,s;
    long t;
    printf("请输入进站人数n:");
    scanf("%d",&n);
    t=time(0)%1000;
    srand(t);                       //随机数发生器初始化
    printf("%d人进站所需时间约为：",n);
    for(t=0,i=1;i<=n;i++)
      t=t+rand()%61+20;            //随机数rand()%(b-a+1)+a    计算进站时间总和
    m=t/600;
    s=(t%600)/10;
    printf("%d分%d秒.\n",m,s);
    return 0; 
} 

 

汉诺塔移动过程的递归程序设计

设移动n个盘的汉诺塔需g(n)次完成。分以下三步骤：

\1. 首先将n个盘上面的n-1个盘子借助c桩从a桩移到b桩上，需g(n-1)次

\2. 然后将a桩上第n个盘子（即最大的盘）移到c桩上（1次）

\3. 最后将b桩上的n-1个盘子借助a桩移到c桩上，需g(n-1)次

因而有递归关系：g(n)=2*g(n-1)+1 g(1)=1

#include<stdio.h> 
​
int x = 0;
​
void hnt(int n, char piv, char tar, char other) {
    if(n <= 0) {
        return ;
    }
    hnt(n-1, piv, other, tar);
    x++;
    printf("移动盘子 %d 从木桩 %c 到木桩 %c\n", n, piv, tar);
    hnt(n-1, other, tar, piv);
}
​
int main() {
    int n;
    printf("请输入一共多少个盘子：\n");
    scanf("%d", &n);
    hnt(n, 'A', 'C', 'B');
    printf("一共移动了 %d 次", x);
    return 0;
}
​

素数合环的回溯程序

#include<stdio.h>
#include<math.h>
int main(){
    int t,i,j,k,a[1000],b[500];
    long s;
    printf("请输入整数n:");
    scanf("%d",&n);
    if(n%2>0){   //排除n为奇数时求解 
        printf("不存在%d项素数和环 \n",n);
        return;
    }
    for(k=1;k<=2*n;k++)
    b[k]=0;
    for(k=3;k<=2*n;k+=2){
        for(t=0,j=3;j<=sqrt(k);j+=2)
        if(k%j==0){
            t=1;break;
        }
        if(t==0) b[k]=1;   //奇数k为素数的标记 
    }
    a[1]=1;s=0;i=2;a[i]=2;
    while(1){
        t=1;
        for(j=1;j<i;j++)
          if(a[j]==a[i]||b[a[i]+a[i-1]]!=1){   //出现相同元素或非素时返回 
            t=0;break;
          }
          if(t&&i==n&&b[a[n]+1]==1){     //确保首尾之和为素数 
            printf("%ld: 1",++s);
            for(j=2;j<=n;j++)
             printf(",%d",a[j]);
            printf("\n"); 
          }
          if(t&&i<n){
            i++;a[i]=2;continue;
          }
          while(a[i]==n&&i>1) i--;   //实施迭代回溯 
          if(i>1) a[i]++;
          else break;
    }
    if(s==0) printf("没有搜索到素数和环 \n");
    else printf("前%d个正整数组成以上%ld个素数和环 \n",n,s); 
}
​

 

动态规划求解最小字段和/最大字段和

#include<bits/stdc++.h>
using namespace std;
int main(){
    int i,j,k,t,n,a[10000];
    long s,smin,q[10000];
    t=time(0)%1000;srand(t);  //随机数发生器初始化
    printf("序列中n个正负项，请确定n:");
    scanf("%d",&n);
    printf("序列中%d个整数为：\n",n);
    for(i=1;i<=n;i++){
        t=rand()%40+10;  //随机产生n个整数
        if(t%2==1) a[i]=-1*(t-1)/2;  //把奇数变为负数，大小减半 
        else a[i]=t/2;  //把偶数大小减半 
        printf("%d,",a[i]);  
    } 
    smin=1000;q[0]=0;
    for(j=1;j<=n;j++){
        if(q[j-1]>=0) q[j]=a[j];   //递推求取q[j] 
        else q[j]=q[j-1]+a[j];
        if(q[j]<smin){    //比较得最小值 
            smin=q[j];k=j;
        }
    }
    printf("最小子段和为：%ld",smin);
    for(s=0,i=k;i>=1;i--){    //反推最小和子段的首标i 
        s+=a[i];
        if(s=smin) break;
    }
    printf("最小子段:%d~ %d",i,k);
}
​

 

可拆分背包的贪心程序设计

#include<stdio.h>
#define N 10
int mian(){
    float x[N],c,cw,s,h;
    int i,j,n;
    float w[]={0,32,5,6,7,8};   //各物品原始数据存储 
    float p[]={0,6,7,8,3,4};
    n=5;
    printf("请输入背包载重量c：");
    scanf("%f",&c);
    printf("%d件物品的重量与效益分别为：\n",n);
    for(i=1;i<=n;i++)
     printf("%5.1f,%5.1f;",w[i],p[i]);
    for(i=1;i<=n-1;i++)
    for(j=i+1;j<=n;j++)
      if(p[i]/w[i]<p[j]/w[j])    //按单位重量的效益降序排序
      {h=p[i];p[i]=p[j];p[j]=h;
       h=w[i];w[i]=w[j];w[j]=h;
                  }
    cw=c;s=0;      //cw位背包还可装的重量
    for(i=1;i<=n;i++){
        if(w[i]>cw)
        break;
        x[i]=1.0;   //若w[i]<cw,整体装入 
        cw=cw-w[i];
        s=s+p[i];
    }    
    x[i]=(float)(cw/w[i]);    //若w[i]>cw,装入一部分x[i] 
    s=s+p[i]*w[i];
    printf("\n 装包：");  //输出装包结果 
    for(i=1;i<=n;i++)
      if(x[i]<1)  break;
      else 
      printf("\n 装入重量为%5.1f效益为%5.1f的物品",w[i],p[i]);
    if(x[i]>0 && x[i]<1)
      printf("\n 装入重量为%5.1f效益为%5.1f的物品%5.1f",w[i],p[i],x[i]*100);
    printf("\n 最大收益为%5.1f\n",s);                              
}
​

最长公共子序列

#include<stdio.h>
#define N 100
int main(){
 char x[N], y[N];
    int i,j,m,n,t,w,c[N][N],s[N][N];
    printf("序列x：");scanf("%s",x);
    printf("序列y：");scanf("%s",y);
    for(m=0,i=0;x[i]!='\0';i++) m++;
    for(n=0,i=0;y[i]!='\0';i++) n++;
    for(i=0;i<=m;i++) c[i][n]=0;  //赋边界值 
    for(j=0;j<=n;j++) c[m][j]=0;
    for(i=m-1;i>=0;i--)           //递推计算最优值 
    for(j=n-1;j>=0;j--)
      if(x[i]==y[j]){
        c[i][j]=c[i+1][j+1]+1;
        s[i][j]=1;
      }
      else{
        s[i][j]=0;
        if(c[i][j+1]>c[i+1][j]) c[i][j]=c[i][j+1];
        else c[i][j]=c[i+1][j];
      }
      printf("最长公共子序列的长度为：%d",c[0][0]);   //输出最优值 
      printf("一个最长公共子序列为：");               //构造最优解 
      t=0;w=0;
      for(i=0;i<=m-1;i++)
      for(j=t;j<=n-1;j++)
         if(s[i][j]==1&&c[i][j]==c[0][0]-w){
            printf("%c",x[i]);
            w++;t=j+1;break;
         }
         printf("\n");
}
​

编程

α、β裂变计算公式

 

#include <stdio.h>
int main ()
{
    int t,k;
    long g[100];
    printf("请输入时间t:");
    scanf("%d",&t);
    g[0]=0;
    g[1]=3;
    for(k=2;k<=t;k++)
      g[k]=2*g[k-1]+3*g[k-2];
    printf("%d秒时反应堆中β粒子数为：%ld \n",t,g[t]);
    printf("%d秒时反应堆中α粒子数为：%ld \n",t,g[t-1]);
    return 0;
}