数据挖掘

0 上手前准备

　　首先看数据集意义，确定以哪个数据集为基层数据通过添加特征丰富数据，最后形成训练集。

　　然后看预测结果集的格式，对于二分类问题是形成最终的预测（如0,1）还是预测概率（如5e^-4）。

　　最重要的是要看手册，避免自身操作带来的失误。

1 数据挖掘基础操作

1.1 查看表

p = pd.read_csv('../data/A/test_prof_bill.csv')
p.head()

　　查看表的前五行，方便简单了解数据的大致内容和数值例子。

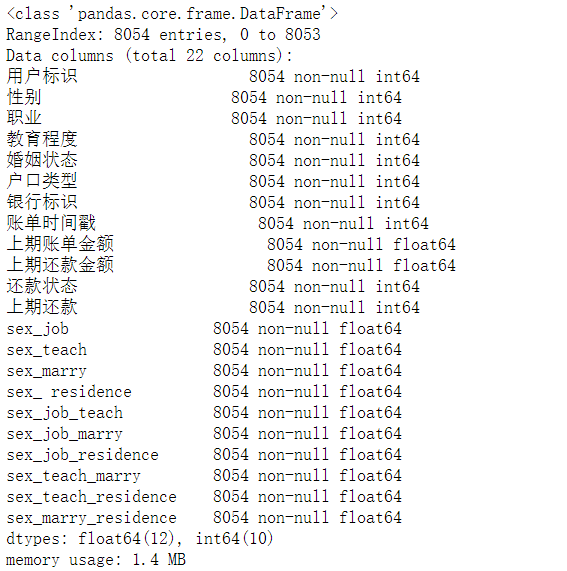
p.info()

　　具体查看表的组成，包括列名，列中元素的类型，空值情况

import os
import seaborn as sns
import matplotlib.pyplot as plt
color = sns.color_palette()
group_df = train_L.标签.value_counts().reset_index()
k = group_df['标签'].sum()
plt.figure(figsize = (12,8))
sns.barplot(group_df['index'], (group_df.标签/k), alpha=0.8, color=color[0])
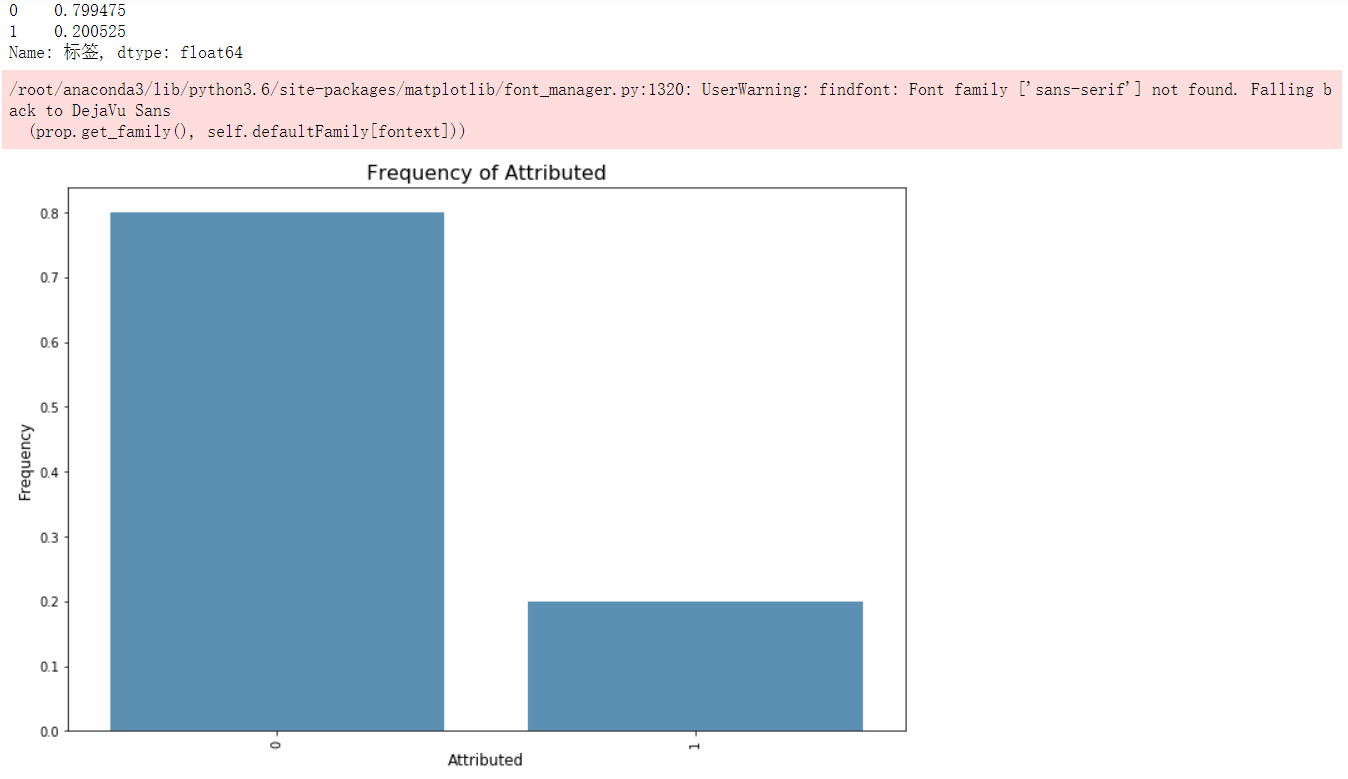
print((group_df.标签/k))
plt.ylabel('Frequency', fontsize = 12)
plt.xlabel('Attributed', fontsize = 12)
plt.title('Frequency of Attributed', fontsize = 16)
plt.xticks(rotation='vertical')
plt.show()

　　表中某一列分布情况概览，这种方法主要用于数据中正负样本的统计，根据统计结果可一选择采样比例。

 1.2 查看各个基础特征对结果的影响因子

colormap = plt.cm.viridis
plt.figure(figsize=(16,16))
plt.title(' The Absolute Correlation Coefficient of Features', y=1.05, size=15)
sns.heatmap(abs(bg.astype(float).corr()),linewidths=0.1,vmax=1.0, square=True, cmap=colormap, linecolor='white', annot=True, )
plt.show()

　　以协方差为衡量指标，绘制可视化界面

 

 1.3 形成新特征

　　仅以一例说明，在本数据中有一行为的七个种类，分别为ABCDEFG，这七种行为的发生次数比例会对结果有不错的影响：

 

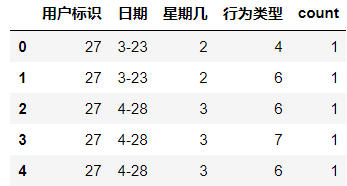
　　现将这七种行为的发生次数按照用户统计，分别统计了用户某一行为的发生次数和用户总行为次数：

count = p1.groupby(['用户标识','行为类型']).count()
maxi = p1.groupby(['用户标识','行为类型']).max()

　　然后将两个临时表合并一下：

merge = pd.merge(c,a,how='left'，on='用户标识') #选择左连接方式

　　计算出来的每一行为几率作为一个特征：

with open('../data/A/behavier_ratio.csv','rt', encoding="utf-8") as csvfile:
    reader = csv.reader(csvfile)
    next(csvfile)
    writefile = open('../data/A/behavier_analy.csv','w+',newline='')
    writer = csv.writer(writefile)
    flag = 1
    user = '1'
    tmp = []
    l = []
    for raw in reader:
        if(raw[0] != user):
            flag = 0
            user = raw[0]
        if(flag == 0):
            if(len(l) != 0):
                writer.writerow(l)
            l = [0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0]
            l[0] = raw[0]
            l[int(raw[1])+1] = raw[4]
            flag = 1
        else:
            l[int(raw[1])+1]=raw[4]
        tmp = l
writer.writerow(tmp)
csvfile.close()
writefile.close()

　　由于数据本身原因，在转变的过程中会产生空值的现象，可以暴力填补：

a.fillna(0，inplace=True)

　　注意，若不添加inplace参数的话是不会在原有基础上进行填补

1.4 无用特征的删除

a = a.drop(['Unnamed: 0'],1)

1.5 结果的存取

　　正常来说，读取这样既可：

total.to_csv('../data/A/total_del.csv')
c = pd.read_csv('../data/A/count_del.csv')

　　但是会出现，表中没有标题行的情况：

b = pd.read_csv('../data/A/bankStatement_analy.csv',header=None, names = ['用户标识','type0_ratio','type1_ratio','type0_money','type1_money'])
a.to_csv('../data/A/test_3.csv',index=False)

2 模型的选取与优化

　　本次选用xgboost模型，使用贝叶斯优化器进行最优参数的选取：

　　对于评价函数，本次比赛使用KS值，因为一直用的是auc评价函数，因此前期吃了不少亏。

 

 　　对于贝叶斯优化器来说，默认的评价函数并没有ks，因此需要自己实现：

def eval_ks(estimator,x,y):
    preds = estimator.predict_proba(x) #获取预测的概率
    preds = preds[:,1]
    fpr, tpr, thresholds = metrics.roc_curve(y, preds) #传入真实值，预测值，获取正样本、负样本以及判别正负样本的阈值
    ks = 0
    for i in range(len(thresholds)):
        if abs(tpr[i] - fpr[i]) > ks:
            ks = abs(tpr[i] - fpr[i])
    print('KS score = ',ks)
    return ks

　　通过查看官方手册可知，自定义评价函数需要传入三个参数

import pandas as pd
import numpy as np
import xgboost as xgb
import lightgbm as lgb
from skopt import BayesSearchCV
from sklearn.model_selection import StratifiedKFold

# SETTINGS - CHANGE THESE TO GET SOMETHING MEANINGFUL
ITERATIONS = 100 # 1000
TRAINING_SIZE = 100000 # 20000000
TEST_SIZE = 40000

# Load data
train = pd.read_csv(
    '../data/step2/train2_1.csv'
)

X = train.drop(['label'],1)
Y = train['label']
bayes_cv_tuner = BayesSearchCV(
    estimator = xgb.XGBClassifier(
        n_jobs = 1,
        objective = 'binary:logistic',
        eval_metric = 'auc',
        silent=1,
        tree_method='approx'
    ),
search_spaces = {
        'learning_rate': (0.01, 1.0, 'log-uniform'),
        'min_child_weight': (0, 10),
        'max_depth': (0, 50),
        'max_delta_step': (0, 20),
        'subsample': (0.01, 1.0, 'uniform'),
        'colsample_bytree': (0.01, 1.0, 'uniform'),
        'colsample_bylevel': (0.01, 1.0, 'uniform'),
        'reg_lambda': (1e-9, 1000, 'log-uniform'),
        'reg_alpha': (1e-9, 1.0, 'log-uniform'),
        'gamma': (1e-9, 0.5, 'log-uniform'),
        'min_child_weight': (0, 5),
        'n_estimators': (50, 100),
        'scale_pos_weight': (1e-6, 500, 'log-uniform')
    },    
    scoring = eval_ks,
    cv = StratifiedKFold(
        n_splits=3,
        shuffle=True,
        random_state=42
    ),
    n_jobs = 3,
    n_iter = ITERATIONS,
    verbose = 0,
    refit = True,
    random_state = 42
)
result = bayes_cv_tuner.fit(X.values, Y.values)
all_models = pd.DataFrame(bayes_cv_tuner.cv_results_)
best_params = pd.Series(bayes_cv_tuner.best_params_)
print('Model #{}\nBest ROC-AUC: {}\nBest params: {}\n'.format(
    len(all_models),
    np.round(bayes_cv_tuner.best_score_, 4),
    bayes_cv_tuner.best_params_
    ))
    
    # Save all model results
clf_name = bayes_cv_tuner.estimator.__class__.__name__
all_models.to_csv('../data/_cv_results.csv')　

 

 　　训练结果是定义的迭代次数中，分数最好的参数配置，使用该参数配置应用于测试集的预测：

import csv
test = pd.read_csv('../data/B/test2_1.csv')
clf = xgb.XGBClassifier(colsample_bylevel= 0.782142304086966, colsample_bytree=  0.9019863190224396, gamma= 0.0001491431487281734, learning_rate= 0.1675067687563292, max_delta_step= 3,max_depth= 10, min_child_weight= 4, n_estimators= 76, reg_alpha= 0.0026534914283041435, reg_lambda= 211.46421106591836, scale_pos_weight= 0.5414848749017023, subsample= 0.8406121867576984)
clf.fit(X,Y)
preds = clf.predict_proba(test) #该函数产生的是概率，predict函数产生的是0,1结果
upload = pd.DataFrame()
upload['客户号'] = test['用户标识']
upload['违约概率'] = preds[:,1] #注意，模型训练出来的结果是两列，第一列是预测为0的概率，第二列是预测为1的概率，根据题意，取为1的概率作为最终概率
upload.to_csv('../data/A/upload.csv',index=False)
with open('../data/A/upload.csv','rt', encoding="utf-8") as csvfile:
    reader = csv.reader(csvfile)
    next(csvfile)
    writefile = open('../data/A/up.csv','w+',newline='')
    writer = csv.writer(writefile)
    for raw in reader:
        writer.writerow(raw)
csvfile.close()
writefile.close()