静态区间(一维和二维)最值问题(ST表,单调队列,RMQ,树状数组,线段树)

//https://www.luogu.com.cn/problem/P3865

//类似于动态规划和压状dp
//f[i][j]是从i位置开始到i+2^j-1的区间内的最大值,一步一步更新所有区间的最大值
//有距离限制,即到达某一位置时,j可能过大导致越界,所以对与每个i,有区间属于:[1,n-(2^j-1)]
//则j的受限范围为:j≤n⇔j≤lg[n]，其中lg[n]表示n关于底数2的对数向下取整，可以递推求得。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m,x,y,a[N],lg[N],f[N][21];
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
    return x*f;
}
int main()
{
    n=read(),m=read(); lg[1]=0;
    for(int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
    for(int i=1;i<=n;i++) f[i][0]=read();
    for(int j=1;j<=lg[n];++j){
        for(int i=1;i<=n-(1<<j)+1;++i)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    }
    while(m--){
        x=read(),y=read();
        int pos=lg[y-x+1];
        cout<<max(f[x][pos],f[y-(1<<pos)+1][pos])<<endl;
    }
}

 

预处理阶段

首先你应该知道的是，ST表是利用倍增思想来缩短时间的。而倍增就体现在他数组的定义中：对于 $ f[i][j] $ ，指的是在序列的第 $ i $ 项，向后 $ 2^j $ 个元素所包含序列间的最大值。

对于 $ j=1 $ ，我们可以画出这么一个图，其下标即为 $ i $ ：

 

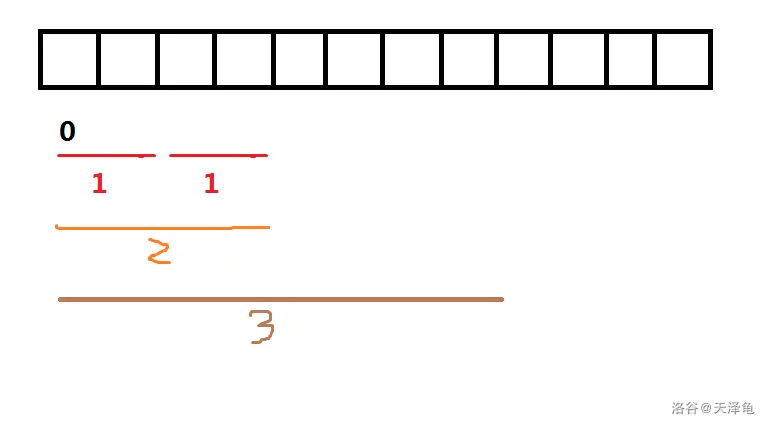
那么对于当前 $ i $ 转移其实很明显了，我们可以直接考虑将两个小区间的答案合并，即为这个大区间的值；如图中 $ f[1][2] $ 即可由 $ (f[1][1], f[3][1]) $ 中的最大值来转移

$f[i][j] = \max(f[i][j-1], f[i+2^{(j-1)}][j-1])$

 

其中 $2$ ^ $(j-1)$ 也可写为 $ (1 << (j-1)) $ ，这里位运算会更方便也会更快。

这个式子告诉我们，ST表类似于区间DP，是由两个小区间合并上来的。所以应该先枚举区间长度 $ l $ （这里即为 $ j $ ），再枚举 $ i $ 。

然后一个问题应运而生了：我们这个转移方程有没有边界呢？

 

不妨来看一下 $ i=6 $ 的图：

 

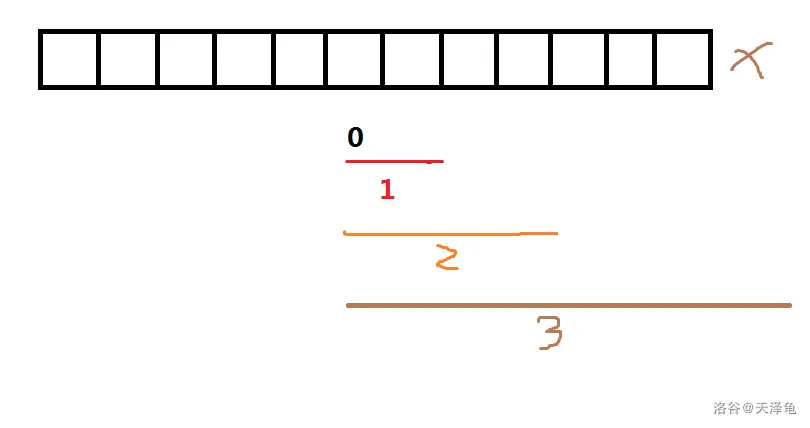
可以看出在 $ i=6 $ 时， $ j=3 $ 的范围是 $ [6, 13(6+2^3)] $ ，已经超出了我们数据的范畴。所以当 $ j=3 $ 时， $ i $ 只能取到 $ [1, 5(12-2^3+1)] $ 。

由上例再根据转移方程，不难看出当 $ j $ 确定时， $ i $ 的范围受限在 $ [1, n-2^j+1] $ 。

那么又根据 $ j=1 $ 时的情况，可知 $ j $ 应满足:   $ 2^j ≤ n ⇔ j ≤ lg[n] $ .

 

其中 $lg[n]$  表示 $n$ 关于底数 2 的对数向下取整，可以递推求得。

预处理代码:

scanf("%d%d", &n, &m);
lg[1] = 0;
for (int i = 2; i <= n; i++) lg[i] = lg[i>>1] + 1; // 求 lg[i] 函数。

for (int i = 1; i <= n; i++) scanf("%d", &f[i][0]);
for (int j = 1; j <= lg[n]; j++)
    for (int i = 1; i <= n-(1<<j)+1; i++) { // 注意两个边界
        f[i][j] = max(f[i][j-1], f[i+(1<<(j-1))][j-1]);
    }

 

单调队列模板(滑动窗口):

//https://www.luogu.com.cn/problem/P1886?contestId=134839

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int n,m,hh,tt,a[N],q[N],k;
int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>a[i];
    hh=1,tt=0;
    for(int i=1;i<=n;i++){
        while(hh<=tt&&q[hh]<i-k+1) hh++;
        while(hh<=tt&&a[q[tt]]>=a[i]) tt--;
        q[++tt]=i;
        if(i>=k) cout<<a[q[hh]]<<' ';
    }
    cout<<endl;
    hh=1,tt=0;
    for(int i=1;i<=n;i++){
        while(hh<=tt&&q[hh]<i-k+1) hh++;
        while(hh<=tt&&a[q[tt]]<a[i]) tt--;
        q[++tt]=i;
        if(i>=k) cout<<a[q[hh]]<<' ';
    }
    return 0;
}

单调队列+ST表 例题:

//https://www.luogu.com.cn/problem/P2251
//st表版
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,x,y,lg[N],f[N][21];
int main()
{
    scanf("%d%d",&n,&m);
    lg[1]=0;
    for(int i=1;i<=n;i++) scanf("%d",&f[i][0]);
    for(int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
    for(int j=1;j<=lg[n];j++){
        for(int i=1;i<=n-(1<<j)+1;i++){
            f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]);
        }
    }
    for(int i=1;i<=n-m+1;i++){
        int l=i,r=i+m-1;
        int pos=lg[m+1];
        printf("%d\n",min(f[l][pos],f[r-(1<<pos)+1][pos]));
    }
    return 0;
}

//单调队列版
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n,m,res,hh,tt,a[N],q[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    hh=1,tt=0;
    for(int i=1;i<=n;i++){
        while(hh<=tt&&q[hh]+m<=i) hh++;
        while(hh<=tt&&a[q[tt]]>=a[i]) tt--;
        q[++tt]=i;
        if(i>=m) cout<<a[q[hh]]<<endl;
    }
    return 0;
}

//https://www.luogu.com.cn/problem/P1638
//类 单调队列,每次都维护画的最后一次位置,然后根据最后的位置进行动态的更新
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int num,n,m,res=2e9,hh,h=1,tt,t,a[N],q[N];
map<int,int>mp;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        if(mp[a[i]]==0) num++;
        mp[a[i]]=i;
        while(h<mp[a[h]]) h++;
        if(num==m&&res>i-h+1) res=i-h+1,hh=h,tt=i;
    }
    cout<<hh<<' '<<tt;
    return 0;
}

//https://www.luogu.com.cn/problem/P1440
//只需要在单调区间进行变换之前输出上一步的状态即可

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
int n,m,res,a[N],hh,tt,q[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    hh=1,tt=0;
    for(int i=1;i<=n;i++){
        cout<<a[q[hh]]<<'\n';
        while(hh<=tt&&q[hh]+m<=i) hh++;
        while(hh<=tt&&a[q[tt]]>=a[i]) tt--;
        q[++tt]=i;
    }
    return 0;
}

 

//首先考虑把环变成链,正常思路是i+n,开两倍空间
//由于我们需要先考虑变成链之后如何做,我们需要所得是枚举区间的最值然后得出最小的距离
//所以可以考虑二分答案,在二分答案的时候,会出现,i+mid,i-mid,如果mid较大,i-mid<=0,出现越界
//所以我们要开三倍空间,然后在中间进行二分
//现在回到题目: 为什么要考虑二分?如何维护单调性?

//首先数据范围为:1e5,即nlogn的复杂度,我们需要在很多长度中找出最小的,不免想到二分寻找,反正暴力枚举肯定不行
//既然要二分就要考虑单调性,设我们的f[i]为x,即在x的范围内有一个数大于等于b,也就是我们可以维护区间最大值来进行二分
//由于 i!=j,所以我们要这样二分: [i-x,i-1],[i+1,i+x]即可

//https://www.luogu.com.cn/problem/P7333
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+10;
int n,m,f[N][30],lg[N],b;
bool check(int u,int x,int b)
{
    // i-x,i-1. i+1,i+x
    int pos=lg[x];
    int l=max(f[u-x][pos],f[u-(1<<pos)][pos]);
    int r=max(f[u+1][pos],f[u+x+1-(1<<pos)][pos]);
    if(l>=b||r>=b) return true;
    else return false;
}
int main()
{
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n;
    for(int i=2;i<=3*n;i++) lg[i]=lg[i>>1]+1;
    for(int i=1;i<=n;i++){
        cin>>f[i][0];
        f[i+n][0]=f[i+n+n][0]=f[i][0];
    }
    for(int j=1;j<=lg[3*n];j++)
        for(int i=1;i<=3*n+1-(1<<j);i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    for(int i=1;i<=n;i++){
        int l=1,r=n;
        cin>>b;
        while(l<r){
            int mid=l+r>>1;
            if(check(i+n,mid,b)) r=mid;
            else l=mid+1;
        }
        if(r==n) cout<<-1<<' ';
        else cout<<r<<' ';
    }
    return 0;
}

 

二维滑动窗口:

0子矩阵 - 蓝桥云课 (lanqiao.cn)

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2040,mod=998244353;
int n,m,res,a,b;
int mxr[N][N],mir[N][N],mxc[N],mic[N],mp[N][N];
int q[N],cmx[N],cmi[N];
void get_max(int a[],int f[],int len,int k){
    int hh=0,tt=-1;
    for(int i=1;i<=len;i++){
        while(hh<=tt&&q[hh]+k<=i) hh++;
        while(hh<=tt&&a[q[tt]]<=a[i]) tt--;
        q[++tt]=i,f[i]=a[q[hh]];
    }
}
void get_min(int a[],int f[],int len,int k){
    int hh=0,tt=-1;
    for(int i=1;i<=len;i++){
        while(hh<=tt&&q[hh]+k<=i) hh++;
        while(hh<=tt&&a[q[tt]]>=a[i]) tt--;
        q[++tt]=i,f[i]=a[q[hh]];
    }
}
signed main()
{
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n>>m>>a>>b;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++) cin>>mp[i][j];
    for(int i=1;i<=n;i++)
        get_max(mp[i],mxr[i],m,b),get_min(mp[i],mir[i],m,b);
    int res=0;
    for(int i=b;i<=m;i++){
        for(int j=1;j<=n;j++) cmx[j]=mxr[j][i],cmi[j]=mir[j][i];
        get_max(cmx,mxc,n,a),get_min(cmi,mic,n,a);
        for(int j=a;j<=n;j++) res+=(mxc[j]*mic[j]),res%=mod;
    }
    cout<<res;
    return 0;
}