1.BLDCM的定子绕组可以分为梯形和正弦,根本区别是绕组的不同连接方式使他们产生的反电势不同(梯形/正弦)
2.根据反电势波形,梯形波:直流无刷电机;正弦波:永磁同步电机
3.电机结构和绕组配合,可以形成方波,正弦波磁势。电机学里边 通过分布绕组 短距绕组什么的 将方波的磁动势改变为 正弦波的磁动势,然后三相合成即成为了旋转磁势;如果不短距不分布,那么磁动势是方波,辅之不同的定子绕组通电方式(比如依次导通120°这种),磁动势就不会是正弦的了,就可以形成梯形波的反电势。这也是为什么直流无刷都会强调 集中整距绕组 每极每相槽数为1。
以下为参考例证:
额我也不知道怎么通过方波磁密产生梯形波反电势。。。。
很多参考文献中都是 梯形的磁密波产生梯形反电势,这个是ok的。
对于稀土永磁无刷直流电机,其气隙磁场波形可以是方波、梯形波和正弦波,这和永磁体形状,电机磁路结构和磁钢充磁等有关。对于径向充磁结构,稀土永磁体直接面对均匀气隙。由于稀土永磁体的取向性好,所以可以方便获得具有较好方波形状的气隙磁场,对于方波气隙磁场电机,当定子绕组采用集中整距绕组,即每极每相槽数q=1,方波磁场在定子绕组中感应电势为梯形波
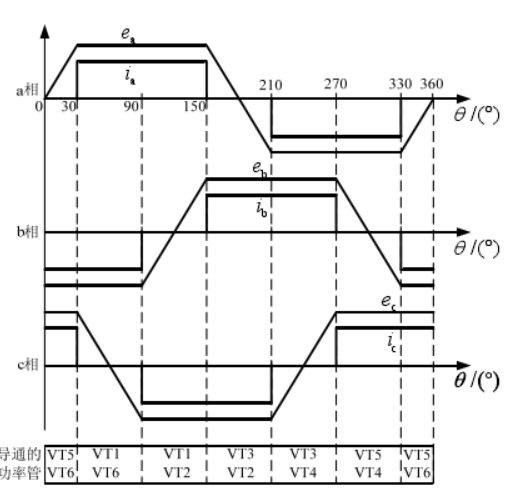
如果从电动机角度来看为什么形成梯形波。比如对于a相,两段平顶波是因为a相分别通正/负电,所以电势基本上等于外加电压。
而在150°-210°这个范围,a相并未通电,所以这段电压是反电势,也就是转子切割定子,所以大小会随着角度改变,当角度为180°,磁场和绕组平行,不切割,所以为0.
想法错误。。因为决定反电势E的是转子,并不是外界电压,导通与否什么的。。
六步梯形波的控制导致无刷电机在扭矩输出有很大的“脉动”特性,就是卖出的力气一抖一抖的,震动大,噪音高,这点不如他的嫡系兄弟永磁同步电机的正弦波控制输出给力;虽然BLDC的起步转矩很大,但不够持久(恒转矩区基本没有),转矩-转速特性曲线还是和有刷电机相同,是线性的;而且还有个老问题,在交流供电场所多的大时代前提下,必须要将正弦波交流电整流成梯形波,控制较复杂,相对于交流电机来说,成本还是有点贵(永磁体是很贵滴,尤其是在海外那些稀土矿比较贫乏的国家,想都不敢想)。所以,论普遍性来说,还是交流电机要更胜一筹。
BLDC和传统直流电机还是有区别的。BLDC是永磁体,所以转矩计算可以套用 T=k*ψs*ψr*sinθ (θ是定转子磁链夹角),当ab相通电,那么定子的磁链方向在这个时间段是不变的,而转子方向是在改变,所以磁链大小不变但是θ变小,产生的转矩并不是平滑的。而对传统的直流电机,由于转子是通直流电,所以T=∑BIL(对所有线圈转矩求和),不存在θ改变这种情况,也不会出现脉动。
而对于交流电机,正弦波控制,可以产生旋转磁场,B=Bm *cos(x-wt) 所以气隙旋转磁场的转速 v=dx/dt=d(wt)/dt=w.可以看出来是匀速的,那么就不会存在 θ改变了。
哈哈哈上述我的猜想居然有论文论证了
参考文献:方波 、 正弦波无刷直流 电机及 永磁同步电机结构 、 性能分析 ——曹荣昌 黄娟
再补充一点吧:
永磁同步电机中矢量控制 iq垂直于磁动势,其实也就是说 定子磁势垂直转子永磁的磁势,时刻保持90°产生的转矩才是最大的,因为一旦不能保持90°,那么就会有去磁分量,转矩就会减小。
但是BLDC没法始终保持定转子磁势相差90°。。。
感觉之前一直走进了一个误区。。EI在不换相时恒定,按理说转矩不会波动,但是按照上面磁动势以及夹角分析,转矩是变的。
很可能!! P=EI T=EI/ω 问题就在转速上。从下图来看,转矩的变化是先增后减,那么P不变的基础上,转速时先减后增。那么这就和BLDC/传统直流电机 的n-T曲线一样了,转矩和n成反比!!
不过话说T的变化也不是很大。。。0.707-1的范围

上面的想法有问题。因为E不变的基础就是转速不变。


