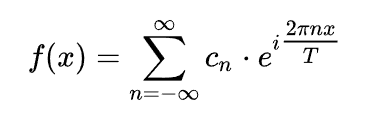先从n维向量空间引申到希尔伯特(无限)向量空间
再由希尔伯特 引入 函数空间
再从函数空间与基去考虑 傅里叶级数
并介绍了其他的函数空间的基♂ 比如泰勒展开 就是多项式基
这些文章给了我们新思路:可以从线性变换去考虑这些东西。
正交化过程的理解:之前一直是死机公式。。。
内积:某一向量在另一向量上投影 与 另一向量 的乘积
先选取第一个向量a,然后对于第二个向量b 就要减去 其在第一个向量上的投影 <a,b>/<a,a>. ab内积除以a的长度

傅里叶级数:针对周期函数,他的表达式是离散的求和,所以频谱图是离散的
傅里叶变换:周期->∞ 也就是傅里叶的一般化。他的表达式是积分 所以频谱图是连续的
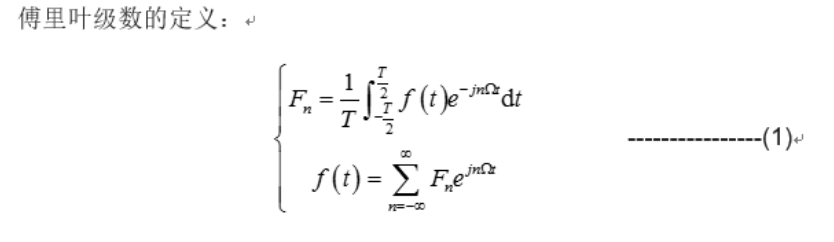


从上述推导可以知道,因为Fn太小了 所以重新定义了频谱密度函数F(jw) 这就好像离散的概率 连续的就是概率密度了一样。于是傅里叶级数中的1/T就被消掉了。2pi是因为T和Ω关系
傅里叶变换中的一系列基其实对应了不同的频率。即时域信号可以分解成一串不同频率正弦信号的叠加。
知乎上马老师 有个视频:不同的频率旋转的圆组合起来能画出任何图像,就是这个道理。这也正好对应了傅里叶级数另一种形式: