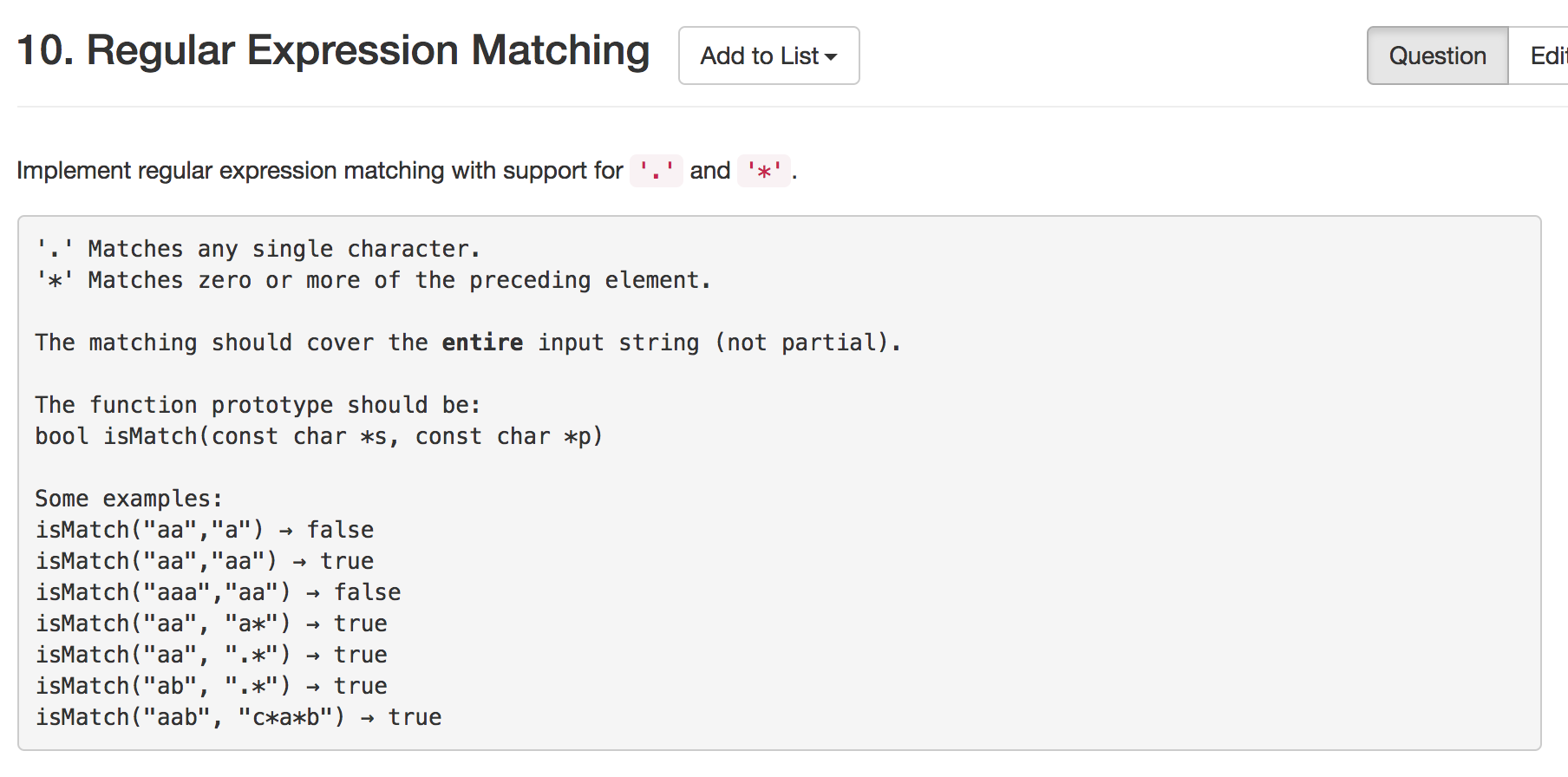
思路
这道题确实有点费劲, 不过我上个暑假也是实现过一个简单的正则表达式引擎的, 所以慢慢分析慢慢写也就写出来了... 我来说下我是怎么想的 :
- 首先我忽略了p或者s为空之类的繁琐corner case, 先想正常情况下的处理可能遇到的问题.
- 主要在于'*'和'.', 处理'.'很简单, '.'就相当于通配符, 可以和任何字符匹配就行了.
- 但是''稍微有点复杂, 因为''可能匹配 >= 0次, 这就意味着实际上我们并不确定到底要匹配多少次, 例如对于"abbbbcd", "abbcd", 这里
b*只能匹配前面的四个b, 而对于"ac", "abc",b*只需要匹配0次. 这里可以这么想, 我们可以尝试着从0此开始匹配, 然后假设它就是匹配0次, 然后对于两组字符串后面的值进行递归匹配, 如果行, 直接返回true, 否则返回false, 那么我们就匹配一次, 以此类推. 但这都是建立在字符串s的当前字符与*的作用字符相同的情况下来执行的.
想到这里我就开始写代码了...
实现
实际实现上, 我为了区分当前是匹配模式(就是匹配中遇到了)和非匹配模式, 使用了一个布尔值star, 同时用starMatch记录匹配的字符. 然后在实际的循环过程中区分是否是star模式, 如果是, 我们按照上面的思路进行, 如果不是, 我们首先考虑这p中的字符的后一个字符是否是, 如果是就进入star模式, 否则就看两个字符是否相等, 此时只有一种情况返回false, 那就是p和s中不同, 另外p种不是通配符.. 然后我具体说下我为什么要提前考虑后一个字符是否是*, 我一开始并不是这样的, 但是后来多次提交, 在这个地方碰到了巨多坑, 所以提前考虑的.
提交
总共提交了7次才AC, 反正各种corner case :
前面的几个就是关于提前考虑*的, 我说几个别的 :
- "", "abc"或者"a", "aabc"或者"", "abc"
- "aaaaa", "a*".
这种你必须要考虑跳出循环的条件, 因为我跳出循环的条件是s和p都没有到结尾. 那么这里会出现, 一个已经到结尾, 一个没到结尾然后跳出循环的情况, 你必须要判断所有的情况, 反正就是贼坑.
代码
public class Solution {
public boolean isMatch(String s, String p) {
boolean star = false;
char starMatch = 0;
char sourceChar, pattenChar;
int i = 0, j = 0;
while(i < s.length() && j < p.length()){
sourceChar = s.charAt(i++);
if(star){
if(starMatch != '.' && sourceChar != starMatch){
star = false;
--i;
}
else{
if(isMatch(s.substring(i - 1), p.substring(j))){
return true;
}
}
continue;
}
pattenChar = p.charAt(j++);
if(j != p.length() && p.charAt(j) == '*'){
star = true;
starMatch = p.charAt(j - 1);
++j;
--i;
}
else if(sourceChar != pattenChar && pattenChar != '.'){
return false;
}
}
if(i == s.length() && j == p.length()) return true;
else if(i == s.length() && p.length() - j > 1 && (p.length() - j) % 2 == 0){
--j;
while((j = j + 2) < p.length()){
if(p.charAt(j) != '*') return false;
}
return true;
}
else if(j == p.length() && star){
while (i < s.length()){
if(starMatch != '.' && s.charAt(i) != starMatch) return false;
++i;
}
return true;
}
else{
return false;
}
}
}
最佳实现
看了下讨论区好像可以用DP做, 我试试看, 如果明天没想出来就参考别人的了...
考虑了一番发现想不出来, 于是看了下别人的做法, 真的是牛逼啊. 这道题总结来看其实只有这么三种情况 :
- p此时长度超过1并且第二个字母是
*, 这说明此时p的前两个字母可以匹配大于等于0个字母, 同时这里细分下去还有两种情况 :- 如果此时p的第一个字母是
.或者与s的第一个字母不相同的话, 那么此时p的前两个字母只能匹配0个字母. - 否则的话可以匹配大于等于0个.
- 如果此时p的第一个字母是
- 如果不是上面那种情况的话, 那么必须要求p的第一个字母是
.或者p和s的首字母相同才能继续往后匹配. - p为空, 此时s必须为空.
所以确实可以用DP写, 用DP速度快但是难想到, 而我这种思路其实是递归实现, 但是其实我的实现比较简陋, 网上看到的最优雅的实现是(这我是真的服) :
public class Solution {
public boolean isMatch(String s, String p) {
if(p.isEmpty()) return s.isEmpty();
if(p.length() > 1 && p.charAt(1) == '*'){
return isMatch(s, p.substring(2)) ||
s.length() > 0 && (p.charAt(0) == '.' || s.charAt(0) == p.charAt(0)) && isMatch(s.substring(1), p);
}
else{
return !s.isEmpty() && (p.charAt(0) == '.' || s.charAt(0) == p.charAt(0)) && isMatch(s.substring(1), p.substring(1));
}
}
}
然后是DP, DP的话, 我个人觉得如果想不到确实很难想, 这要做的多了可能会有一定的敏感度. 这里主要的思路在于 :
dp[i][j]代表的是s的前i个与p的前j个字母的匹配情况, 按照我们上面分的情况, 这里可以这么认为 :
- 如果p的j位置的字母为
*(要注意这里的第n个字母实际是第n+1的位置, 也就是说如果我说前i+1个字母, 那么这串字母的最后一个是第i个字母)- 那么要么p的j位置与j-1位置的字母匹配0次, 这种情况下 : dp[i+1][j+1] = dp[i+1][j-1], 因为此时要想这两个串字符完成匹配, 相当于s的前i+1个与p的前j-1个完成匹配.
- 要么p的j位置与j-1位置的字母匹配1次, 这种情况下 : dp[i+1][j+1] = dp[i+1][j], 因为此时要想这两个串字符完成匹配, 相当于s的前i个与p的前j-1个完成匹配, 然后s的第i个字母和p的第j-1 和 j个字母完成匹配, 换句话说, 也就是s的前i+1个字母和p的前j的字母匹配, 因为第j个字母是
*. - 那么要么p的j位置与j-1位置的字母可能匹配超过1次, 这种情况下 : dp[i+1][j+1] = dp[i][j+1], 因为此时要想这两个串字符完成匹配, 相当于s的前i个与p的前j+1个完成匹配. 那么s的第i个字母怎么办呢? 由于第i个字母仍然等于p的第j-1的字母, 所以仍然匹配, 所以忽略.
- 如果你仔细分析的话, 你可以发现, 其实匹配1次和超过一次是完全可以合并的. 因为匹配0次的情况已经在前面说明排除了, 所以不管你匹配1次还是多次, 实际都是一样的.
- 如果不是
*, 那么只需要判断是否对于位置匹配就行了.
public class Solution {
public boolean isMatch(String s, String p) {
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
// i == 0 && j == 0 true
dp[0][0] = true;
// i != 0 && j == 0 false java will initialize the array to false, so no need to do it manually
// i == 0 && j != 0
for(int i = 1; i < p.length(); i = i + 2){
dp[0][i + 1] = p.charAt(i) == '*' && (i == 1 || dp[0][i - 1]);
}
// i != 0 && j != 0
for(int i = 0; i < s.length(); ++i){
for(int j = 0; j < p.length(); ++j){
if(p.charAt(j) == '*')
//dp[i+1][j+1] = dp[i+1][j-1] || ((dp[i+1][j] || dp[i][j+1]) && (p.charAt(j-1) == '.' || p.charAt(j-1) == s.charAt(i)));
dp[i+1][j+1] = dp[i+1][j-1] || (dp[i][j+1] && (p.charAt(j-1) == '.' || p.charAt(j-1) == s.charAt(i)));
else
dp[i+1][j+1] = (p.charAt(j) == '.' || p.charAt(j) == s.charAt(i)) && dp[i][j];
}
}
return dp[s.length()][p.length()];
}
}



