2.3 整数运算
2.31 无符号加法
无符号数的加法, 总的来说有一下规则 : 对于两个w位的无符号数x, y相加, 如果 x + y < 2w (这个值之上包括这个值都是w位无符号数无法表示的), 那么他们的值得x + y, 如果x + y超出了这个范围, 那么就造成了溢出, 此时x + y 的值等于 x + y - 2w (实际上是x + y mod 2w, 对于加法而言只可能溢出到w位, 所以这里两者等价)... 溢出之后有一个很明显的特征就是得出来的结果小于两个数中的任何一个... 这一点也很容易证明 :
对于溢出有 : s = x + y - 2w, 因为x, y显然小于2w, 那么 s = x + (y - 2w) 或者 s = y + (x- 2w), 显然 y 加上一个负数当然要小于 y... 所以判断是否发生溢出可以这么写 :
1 int uadd_ok(unsigned x, unsigned y){ 2 return x + y >= x;
3 // 之所以不用写出 x + y >= x && x + y >= y 是因为 x + y的结果要么大于等于x, y要么小于x 并且小于 y... 4 }
2.32 补码加法
对于补码的加法其实有如下规则 :
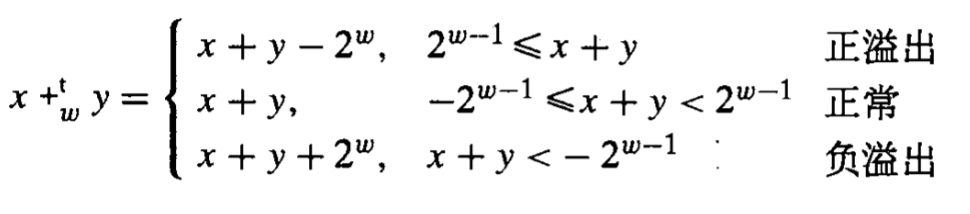
我认为这个也很好理解, 当两个补码 x, y相加的结果超过了 w-1位所能表示的范围, 那么自然这个值需要w位来表示, 然而对于有符号数第w位是作为符号位, 它的权值正好是一个负数, 这样计算出的结果显然不符合正常规律, 即发生了正溢出. 同理也可理解负溢出... 总结一下所以判断是否发生溢出可以这么写 :
int tadd_ok(int x, int y){ return !((x > 0 && y > 0 && x + y < 0) || (x < 0 && y < 0 && x + y >= 0)) }
总结一下是这样的 : 无符号数溢出会得到正数或者0 , 但是无论得到什么, 都会小于两个加数; 有符号数发生溢出只有两种情况, 一种是得到大于等于0的数, 此时这两个数必定是负数, 另一种是得到小于0的数, 此时这两个数一定是正数.
2.3.3 补码的非
这个我感觉其实很简单, 只不过最感觉翻译成补码的非有点别扭(因为它C语言中的~也就是位运算中的取反其实没什么关系, 同时和逻辑运算中的!也没关系), 这里的非就是求相反数(就是求与之相加等于0的数), 除了-2w-1其他的所有值都是直接进行取负操作, 而对于这个数则是其本身, 也就是在w位的情况下, 表示范围内的下限值(最小值)的非是本身, 其他直接取负即可.
两种求补码的非得位级表示的方法, 我个人习惯第二种, 更快更不容易出错...
1. 对于X求非的话 直接 ~X + 1
2. 从lsb开始的第一个1之前的位包括这个1都保持不变, 之后全部取反即可...
2.34 无符号乘法
无符号乘法其实和加法区别不大, 都很简单, 理论上w位的两个无符号数字相乘将会需要2w为来进行表示, 但事实上, 由于只有w位来表示结果, 那么结果只能是这样的 :
2.35 补码乘法
从位级表示来看, 补码乘法和无符号乘法是一致的, 这样做的好处是机器可以使用同一套指令来进行有符号和无符号数的乘法, 也就是说在这种得计算的过程其实是这样的(也就是说区别就在于解释方式, 其实位级表示一模一样) :
那么我们如何来证明这样用来算无符号数的指令在处理有符号(补码)数时也符合数学规律呢? 换句话说, 形如-1 * 2 = -2 使用这种计算方式也应该得出正确答案, 结果我们发现x, y(带撇的)做乘法之后按照补码的方式进行解释其实和补码是一样的, 这时说明这种做法是正确的.
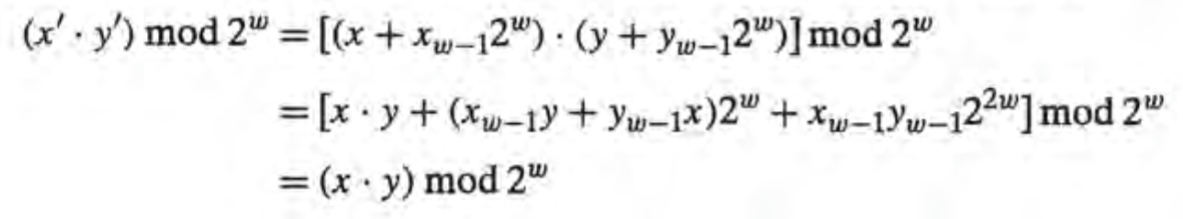
2.35证明很简单就不写了, 2.36我一开始的答案如下(注意我的答案是错误答案) :
1 int tmult_ok(int x, int y){ 2 long long p = (long long)x * y; 3 p = p >> 32; 4 return p == 0 || p == -1; 5 }
参考答案是直接3, 4 行 改成了 return p == (int)p, 一开始我认为效果应该是一样的, 其实不然, 比如对于高32位都是1, 低32位中的最高位是0的情况, 我的函数判断结果为没有溢出, 其实已经溢出了. 所以参考答案是对的.
2.37题考察的其实是malloc函数的参数, 题目本身作为背景故事了解吧, 没多大意思...
2.36 乘以常数
大多数机器中, 整数乘法指令相当慢(需要10个或者更多时钟周期, 加法减法位级以及移位运算只需要1个时钟周期), 所以编译器尝试着用移位和加法来代替乘法, 这是一种重要的优化手段. 例如将 x * 14 优化成为 (x << 3) + (x << 2) + (x << 1) 或者 (x << 4) - (x << 1), 这一部分我个人认为不是特别重要, 只需要知道机器以及编译器内部存在这样的优化即可.
2.37 除以2的幂
除法比乘法更慢(需要30个或者更多周期) , 整数除法有个特性就是向0舍入, 我们先看无符号数, 比如对于4位机器数, 1101(13) 右移动1位(除以2), 结果是0110 (6), 是符合的... 但是对于有符号数, 其在正数区间内也是符合的, 但是在负数区间内却不符合, 如刚在这个例子1101(-3)右移动1位(除以2), 结果是 1110(-2) 而不是预期的 -1...
这是对无符号数位移与除法等价的证明 :
其实这个式子同样适用与补码, 但是为什么偏偏补码为负数的时候会出问题呢? 首先我们要搞清楚这样一个事实, 无论是有符号还是无符号数, 底层的实现是相同的, 也就是说上述推倒在于补码也是通用的, 站在全局的角度来看, 当得到的无符号数越大时, 其补码也就是越大(-1对应最大的无符号数), 问题就在这里, 对于正数来说, 舍去了x两撇那部分, 数值更小了, 当然是更接近零, 但是对于负数则恰好相反, 所以出问题了... 问题就出在移位运算其实是地板除(floor division) 而对于补码负数来说, 他所需要的其实是ceil division, 所以解决思路应该是如何将 x/y (x < 0, y > 0) 转化为等效的移位运算... 书中这一块讲的很好 :
但是除法和乘法在这里有点不同在于, 不像乘法, 并不是任何一个x/k(k为常数)都能使用移位运算来实现. 一块我认为也是知道这么一回事, 就行了, 但是这练习感觉出的还是挺不错的, 就顺带着做了... 2.42 :
int div16(int x){ return (x + ((x >> 31) & 15)) >> 4; }
2.3.8 关于整数运算的最后的思考
计算机执行的整数运算实际上是一种模运算形式, 表示数字的有限字长限制了可能的值得取值范围, 结果可能会溢出. 同时补码相当的神奇, 它提供了表示正负数的方法, 同时还是用了与无符号数相同的位级实现. 同时要注意的是unsigned, 他概念上虽然简单, 但是总是会发生一些意想不到的结果...
2.44 :
A : 错误, 当 x == 0X80000000 时, x - 1 > 0 (发生溢出)
B : 对
C : 错误 (可能溢)
D : 对
E : 错误, 当x = 0X80000000, -x == x < 0
F : 对
G : 对 (首先 ux * uy 在位级表示上就是 x * y, 同时 ~y = -y - 1 )
