nyoj素数环

素数环

时间限制：1000 ms  |  内存限制：65535 KB

难度：2

 

描述

有一个整数n，把从1到n的数字无重复的排列成环，且使每相邻两个数（包括首尾）的和都为素数，称为素数环。

为了简便起见，我们规定每个素数环都从1开始。例如，下图就是6的一个素数环。

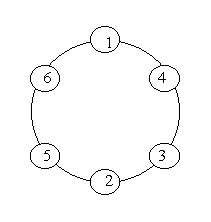
输入

有多组测试数据，每组输入一个n(0<n<20)，n=0表示输入结束。

输出

每组第一行输出对应的Case序号，从1开始。
如果存在满足题意叙述的素数环，从小到大输出。
否则输出No Answer。

样例输入

6
8
3
0

样例输出

Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Case 3:

No Answer

 

#include<string.h>
#include<stdio.h>
int n;
int a[21],b[21];
int fun(int m)
{
    if(m<2)
        return 0;
    for (int i=2; i*i<=m; i++)
    {
        if(m%i==0)
            return 0;
    }
    return 1;
}
void dfs(int s)
{
    if(s==n&&fun(a[1]+a[n]))  //递归边界。别忘了测试第一个数和最后一个数
    {
        for(int i=1; i<=n; i++)
            printf("%d ",a[i]);
        printf("\n");
        return;
    }
    else
    {
        for(int i=2; i<=n; i++)
        {
            if(!b[i]&&fun(i+a[s]))//如果i没有用过，并且与前一个数之和为素数
            {
                a[s+1]=i;
                b[i]=1;
                dfs(s+1);
                b[i]=0;
            }
        }
    }
}
int main()
{
    int t=0;
    while(~scanf("%d",&n),n)
    {
        memset(b,0,sizeof(b));
        a[1]=1;
        t++;
        printf("Case %d:\n",t);
        if(n==1)
        {
            printf("1\n");
            continue;
        }
        if(n%2!=0)
        {
            printf("No Answer\n");
            continue;
        }
        dfs(1);
    }
    return 0;
}