nyoj 234 吃土豆

吃土豆

时间限制：1000 ms  |  内存限制：65535 KB

难度：4

描述

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.


Now, how much qualities can you eat and then get ?

输入

There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M,N<=500.

输出

For each case, you just output the MAX qualities you can eat and then get.

样例输入

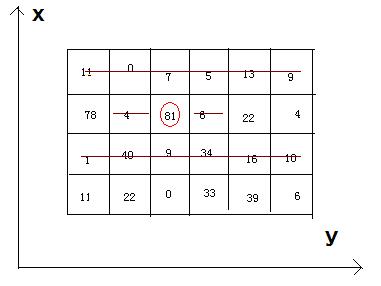
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

样例输出

242

//#include<stdio.h>
//int max(int m,int *a)
//{
//    int i,f[550];
//    for(i=1; i<=m; i++)
//    {
//        if(i==1)  f[i]=a[i];
//        else if(i==2)  f[i]=a[i]>a[i-1]?a[i]:a[i-1];
//        else
//        {
//            f[i]=(f[i-2]+a[i])>f[i-1]?f[i-2]+a[i]:f[i-1];
//        }
//    }
//    return f[m];
//}
////非递归推算法
///*int max(int m,int *a){
//    if(m==1)return a[1];
//    if(m==2)return a[2]=a[1]>a[2]?a[1]:a[2];
//    return max(m-2,a)+a[m]>max(m-1,a)?max(m-2,a)+a[m]:max(m-1,a);
//}*/
//
////递归分制算法
//int main()
//{
//    int a[510],b[510],i,j,m,n;
//    while(scanf("%d %d",&n,&m)==2)
//    {
//        for(i=1; i<=n; i++)
//        {
//            for(j=1; j<=m; j++)
//            {
//                scanf("%d",&a[j]);
//            }
//            b[i]=max(m,a);
//        }
//        printf("%d\n",max(n,b));
//    }
//    return 0;
//}






#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int map,dp[510],R[510][510];
int main()
{
    int m,n,i,j;
    while(~scanf("%d %d",&m,&n))
    {
        memset(R,0,sizeof(R));
        memset(dp,0,sizeof(dp));
        for(i=3; i<m+3; ++i) //把n,m都扩大2，方便dp
        {
            for(j=3; j<n+3; ++j)
            {
                scanf("%d",&map);
                R[i][j]=max(R[i][j-2],R[i][j-3])+map; //累积i行到j列的最大和
            }
        }
        for(i=3; i<m+3; ++i)
        {
            dp[i]=max(dp[i-2],dp[i-3])+max(R[i][n+1],R[i][n+2]); //累积到i行的最大和
        }
        printf("%d\n",max(dp[m+1],dp[m+2]));
    }
    return 0;
}