求最近点对
问题描述
在 应 用 中,常 用 诸 如 点、圆 等 简 单 的 几 何 对 象 代 表 现 实 世 界 中 的实 体 。 在涉 及 这 些 几 何 对 象 的 问 题 中 ,常 需 要 了 解 其 邻 域 中 其 他 几 何 对 象 的 信 息。例 如 ,在 空 中 交 通 控 制 问 题 中 ,若 将 飞 机 作 为 空 间 中 移 动 的 一 个 点 来 看 待,则 具 有 最 大 碰 撞 危 险 的 2 架 飞 机 , 就 是 这 个 空 间 中 最 接 近 的 一 对 点 。 这 类 问 题 是 计 算 几 何 学 中 研 究 的 基 本 问 题 之 一 。 下 面 我 们 着 重 考 虑 平 面 上 的 最 接 近 点 对 问 题。
最接近点对问题的提法是:给定平面上n个点,找其中的一对点,使得在n个点的所有点对中,该点对的距离最小。
严格地说,最接近点对可能多于1对。为了简单起见,这里只限于找其中的一对。
参考解答
这个问题很容易理解,似乎也不难解决。我们只要将每一点与其他n-1个点的距离算出,找出达到最小距离的两个点即可。然而,这样做效率太低,需要O(n2)的计算时间。在问题的计算复杂性中我们可以看到,该问题的计算时间下界为Ω(nlogn)。这个下界引导我们去找问题的一个θ(nlogn)算法。
这 个 问 题 显 然 满 足 分 治 法 的 第 一 个 和 第 二 个 适 用 条 件 , 我 们 考 虑 将 所 给 的 平 面 上 n个 点 的 集 合 S 分 成 2 个 子 集 S1 和 S2,每 个 子 集 中 约 有 n/2 个 点,·然 后 在 每 个 子 集 中 递 归 地 求 其 最 接 近 的 点 对 。在 这 里 ,一 个 关 键 的 问 题 是 如 何 实 现 分 治 法 中 的 合 并 步 骤 ,即 由 S1 和 S2 的 最 接 近 点 对 ,如 何 求 得 原 集 合 S 中 的 最 接 近 点 对 ,因 为 S1 和 S2 的 最 接 近 点 对 未 必 就 是 S 的 最 接 近 点 对 。 如 果 组 成 S 的 最 接 近 点 对 的 2 个 点 都 在 S1 中 或 都 在 S2 中 , 则 问 题 很 容 易 解 决 。 但 是 , 如 果 这 2 个 点 分 别 在 S1 和 S2 中,则 对 于 S1 中 任 一 点 p,S2 中 最 多 只 有 n/2 个 点 与 它 构 成 最 接 近 点 对 的 候 选 者 , 仍 需 做 n2/4 次 计 算 和 比 较 才 能 确 定 S 的 最 接 近 点 对 。 因 此 ,依 此 思 路 , 合 并 步 骤 耗 时 为 O(n2)。整 个 算 法 所 需 计 算 时 间 T(n) 应 满 足:
T(n)=2T(n/2)+O(n2)
它的解为T(n)=O(n2),即与合并步骤的耗时同阶,显示不出比用穷举的方法好。从解递归方程的套用公式法,我们看到问题出在合并步骤耗时太多。这启发我们把注意力放在合并步骤上。
为了使问题易于理解和分析,我们先来考虑一维的情形。此时S中的n个点退化为x轴上的n个实数x1,x2,..,xn。最接近点对即为这n个实数中相差最小的2个实数。我们显然可以先将x1,x2,..,xn排好序,然后,用一次线性扫描就可以找出最接近点对。这种方法主要计算时间花在排序上,因此如在排序算法中所证明的,耗时为O(nlogn)。然而这种方法无法直接推广到二维的情形。因此,对这种一维的简单情形,我们还是尝试用分治法来求解,并希望能推广到二维的情形。
假设我们用x轴上某个点m将S划分为2个子集S1和S2,使得S1={x∈S|x≤m};S2={x∈S|x>m}。这样一来,对于所有p∈S1和q∈S2有p
递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2},并设δ=min{|p1-p2|,|q1-q2|},S中的最接近点对或者是{p1,p2},或者是{q1,q2},或者是某个{p3,q3},其中p3∈S1且q3∈S2。如图1所示。
 图1 一维情形的分治法
图1 一维情形的分治法
我 们 注 意 到 , 如 果 S 的 最 接 近 点 对 是 {p3,q3},即 |p3-q3|<δ,则 p3 和 q3 两 者 与 m 的 距 离 不 超 过 δ ,即 |p3-m|<δ,|q3-m|<δ,也 就 是 说 ,p3∈(m-δ,m],q3∈(m,m+δ]。由 于 在 S1 中,每 个 长 度 为 δ 的 半 闭 区 间 至 多 包 含 一 个 点 ( 否 则 必 有 两 点 距 离 小 于 δ ) , 并 且m 是 S1 和 S2 的 分 割 点,因 此 (m-δ,m] 中 至 多 包 含 S 中 的 一 个 点 。 同 理 , (m,m+δ]中 也 至 多包 含 S 中 的 一 个 点 。 由 图1 可 以 看出 ,如 果 (m-δ,m] 中 有 S 中 的 点 ,则 此 点 就 是 S1 中 最 大 点 。 同 理 ,如 果 (m,m+δ] 中 有 S 中 的 点 , 则 此 点 就 是 S2 中 最 小 点 。因 此 ,我 们 用 线 性 时 间 就 能 找 到 区 间 (m-δ,m] 和 (m,m+δ] 中 所 有 点 , 即 p3 和 q3。从 而 我 们 用 线 性 时 间 就 可 以 将 S1的 解 和 S2 的 解 合 并 成 为 S 的 解 。 也 就 是 说 , 按 这 种 分 治 策 略 , 合 并 步 可 在 O(n) 时 间 内 完 成 。 这 样 是 否 就 可 以 得 到 一 个 有 效 的 算 法 了 呢 ? 还 有 一 个 问 题 需 要 认 真 考 虑 , 即 分 割 点 m 的 选 取,及 S1 和 S2 的 划 分 。 选 取 分 割 点 m 的 一 个 基 本 要 求 是 由 此 导 出 集 合 S 的 一 个 线 性 分 割 ,即S=S1∪S2 ,S1∩S2=Φ,且S1{x|x≤m};S2{x|x>m}。容 易 看 出 , 如果 选 取
m=[max(S)+min(S)]/2,可 以 满 足 线 性 分 割 的 要 求 。 选 取 分 割 点 后, 再 用 O(n) 时 间 即 可 将 S 划 分 成 S1={x∈S|x≤m}和S2={x∈S|x>m}。然 而,这 样 选 取 分 割 点 m , 有 可 能 造 成 划 分 出 的 子 集 S1 和 S2 的 不 平 衡 。 例 如 在 最 坏 情 况 下,|S1|=1,|S2|=n-1, 由 此 产 生 的 分 治 法 在 最 坏 情 况 下 所 需 的 计 算 时 间 T(n) 应 满 足 递 归 方 程:
T(n)=T(n-1)+O(n)
它的解是T(n)=O(n2)。这种效率降低的现象可以通过分治法中"平衡子问题"的方法加以解决。也就是说,我们可以通过适当选择分割点m,使S1和S2中有大致相等个数的点。自然地,我们会想到用S的n个点的坐标的中位数来作分割点。在选择算法中介绍的选取中位数的线性时间算法使我们可以在O(n)时间内确定一个平衡的分割点m。
至此,我们可以设计出一个求一维点集S中最接近点对的距离的算法CPAIR1如下。
function CPAIR1(S);
begin
if |S|=2
then δ=|x[2]-x[1]| // x[1..n]存放的是S中n个点的坐标
else if (|S|=1)
then δ:=∞
else
begin
m:=S中各点的坐标值的中位数;
构造S1和S2,使S1={x∈S|x≤m},S2={x∈S|x>m}; δ1:=CPAIRI(S1); δ2:=CPAIRI(S2);
p:=max(S1); q:=min(S2);
δ:=min(δ1,δ2,q-p);
end;
return(δ);
end;
由以上的分析可知,该算法的分割步骤和合并步骤总共耗时O(n)。因此,算法耗费的计算时间T(n)满足递归方程:
解此递归方程可得T(n)=O(nlogn)。
这个算法看上去比用排序加扫描的算法复杂,然而这个算法可以向二维推广。
下面我们来考虑二维的情形。此时S中的点为平面上的点,它们都有2个坐标值x和y。为了将平面上点集S线性分割为大小大致相等的2个子集S1和S2,我们选取一垂直线l:x=m来作为分割直线。其中m为S中各点x坐标的中位数。由此将S分割为S1={p∈S|px≤m}和S2={p∈S|px>m}。从而使S1和S2分别位于直线l的左侧和右侧,且S=S1∪S2 。由于m是S中各点x坐标值的中位数,因此S1和S2中的点数大致相等。
递归地在S1和S2上解最接近点对问题,我们分别得到S1和S2中的最小距离δ1和δ2。现设δ=min(δ1,δ1)。若S的最接近点对(p,q)之间的距离d(p,q)<δ则p和q必分属于S1和S2。不妨设p∈S1,q∈S2。那么p和q距直线l的距离均小于δ。因此,我们若用P1和P2分别表示直线l的左边和右边的宽为δ的2个垂直长条,则p∈P1,q∈P2,如图2所示。
 图2 距直线l的距离小于δ的所有点
图2 距直线l的距离小于δ的所有点
在一维的情形,距分割点距离为δ的2个区间(m-δ,m](m,m+δ]中最多各有S中一个点。因而这2点成为唯一的末检查过的最接近点对候选者。二维的情形则要复杂些,此时,P1中所有点与P2中所有点构成的点对均为最接近点对的候选者。在最坏情况下有n2/4对这样的候选者。但是P1和P2中的点具有以下的稀疏性质,它使我们不必检查所有这n2/4对候选者。考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有d(p,q)<δ。满足这个条件的P2中的点有多少个呢?容易看出这样的点一定落在一个δ×2δ的矩形R中,如图3所示。
 图3 包含点q的δ×2δ的矩形R
图3 包含点q的δ×2δ的矩形R
由δ的意义可知P2中任何2个S中的点的距离都不小于δ。由此可以推出矩形R中最多只有6个S中的点。事实上,我们可以将矩形R的长为2δ的边3等分,将它的长为δ的边2等分,由此导出6个(δ/2)×(2δ/3)的矩形。如图4(a)所示。
 图4 矩形R中点的稀疏性
图4 矩形R中点的稀疏性
若矩形R中有多于6个S中的点,则由鸽舍原理易知至少有一个δ×2δ的小矩形中有2个以上S中的点。设u,v是这样2个点,它们位于同一小矩形中,则
因此d(u,v)≤5δ/6<δ 。这与δ的意义相矛盾。也就是说矩形R中最多只有6个S中的点。图4(b)是矩形R中含有S中的6个点的极端情形。由于这种稀疏性质,对于P1中任一点p,P2中最多只有6个点与它构成最接近点对的候选者。因此,在分治法的合并步骤中,我们最多只需要检查6×n/2=3n对候选者,而不是n2/4对候选者。这是否就意味着我们可以在O(n)时间内完成分治法的合并步骤呢?现在还不能作出这个结论,因为我们只知道对于P1中每个S1中的点p最多只需要检查P2中的6个点,但是我们并不确切地知道要检查哪6个点。为了解决这个问题,我们可以将p和P2中所有S2的点投影到垂直线l上。由于能与p点一起构成最接近点对候选者的S2中点一定在矩形R中,所以它们在直线l上的投影点距p在l上投影点的距离小于δ。由上面的分析可知,这种投影点最多只有6个。因此,若将P1和P2中所有S的点按其y坐标排好序,则对P1中所有点p,对排好序的点列作一次扫描,就可以找出所有最接近点对的候选者,对P1中每一点最多只要检查P2中排好序的相继6个点。
至此,我们可以给出用分治法求二维最接近点对的算法CPAIR2如下:
function CPAIR2(S);
begin
if |S|=2
then δ:=S中这2点的距离
else if |S|=0
then δ:=∞
else
begin
m:=S中各点x坐标值的中位数; 构造S1和S2,使S1={p∈S|px≤m}和S2={p∈S|px>m}
δ1:=CPAIR2(S1);δ2:=CPAIR2(S2);
δm:=min(δ1,δ2);
设P1是S1中距垂直分割线l的距离在δm之内的所有点组成的集合, P2是S2中距分割线l的距离在δm之内所有点组成的集合。将P1和P2中的点依其y坐标值从小到大排序,并设P1*和P2*是相应的已排好序的点列;
通过扫描P1*以及对于P1*中每个点检查P2*中与其距离在δm之内的所有点(最多6个)可以完成合并。当P1*中的扫描指针逐次向上移动 时,P2*中的扫描指针可在宽为2δm的一个区间内移动。设δl是按 这种扫描方式找到的点对间的最小距离;
δ=min(δm,δl);
end;
return(δ);
end;
下面我们来分析一下算法CPAIR2的计算复杂性。设对于n个点的平面点集S,算法耗时T(n)。算法的第1步和第5步用了O(n)时间,第3步和第6步用了常数时间,第2步用了2T(n/2)时间。若在每次执行第4步时进行排序,则在最坏情况下第4步要用O(nlogn)时间。这不符合我们的要求。因此,在这里我们要作一个技术上的处理。我们采用设计算法时常用的预排序技术,即在使用分治法之前,预先将S中n个点依其y坐标值排好序,设排好序的点列为P*。在执行分治法的第4步时,只要对P*作一次线性扫描,即可抽取出我们所需要的排好序的点列P1*和P2*。然后,在第5步中再对P1*作一次线性扫描,即可求得δl。因此,第4步和第5步的两遍扫描合在一起只要用O(n)时间。这样一来,经过预排序处理后的算法CPAIR2所需的计算时间T(n)满足递归方程:
显而易见T(n)=O(nlogn),预排序所需的计算时间为O(n1ogn)。因此,整个算法所需的计算时间为O(nlogn)。在渐近的意义下,此算法已是最优的了。
求点集中的最近点对有以下两种方法:
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,设计算法找出集合S中距离最近的点对。
1、蛮力法(适用于点的数目比较小的情况下)
1)算法描述:已知集合S中有n个点,一共可以组成n(n-1)/2对点对,蛮力法就是对这n(n-1)/2对点对逐对进行距离计算,通过循环求得点集中的最近点对:
2)代码描述:
double MinDistance = double.maxvalue; //设置一个MinDistance存储最近点对的距离,初始值为无穷大
int PointIndex1,PointIndex2; //设置PointIndex1,PointIndex2分别存储最近点对的两个点编号
for (i=1; i< n; i++) //循环计算n(n-1)/2对点对的距离
{
for (j=i+1; j<=n; j++)
{
double PointDistance = Distance(S[i],S[j]); //求得point i和point j之间的距离
if PointDistance < MinDistance; //如果当前点对距离小于最小点对距离,则设置最小点对距离等于当前点对距离
{
MinDistance = PointDistance;
PointIndex1 = i;
PointIndex2 = j;
}
}
}
}
3)算法时间复杂度:算法一共要执行 n(n-1)/2次循环,因此算法复杂度为O(n2)
2、分治法
1)算法描述:已知集合S中有n个点,分治法的思想就是将S进行拆分,分为2部分求最近点对。算法每次选择一条垂线L,将S拆分左右两部分为SL和SR,L一般取点集S中所有点的中间点的x坐标来划分,这样可以保证SL和SR中的点数目各为n/2,
(否则以其他方式划分S,有可能导致SL和SR中点数目一个为1,一个为n-1,不利于算法效率,要尽量保持树的平衡性)
依次找出这两部分中的最小点对距离:δL和δR,记SL和SR中最小点对距离δ = min(δL,δR),如图1:
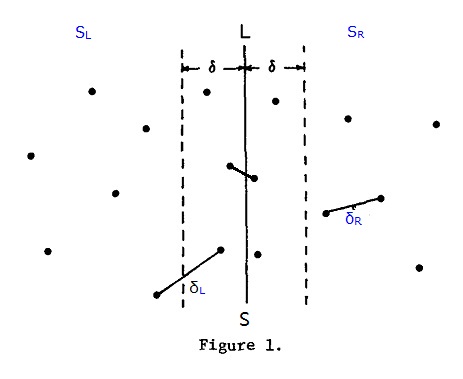
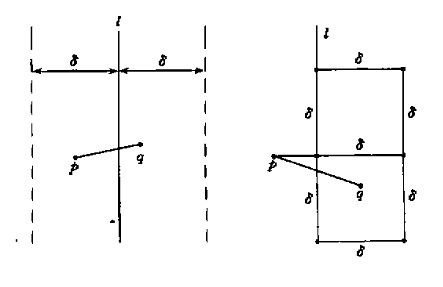
对于SL虚框范围内的p点,在SR虚框中与p点距离小于δ的顶多只有六个点,就是图二右图中的2个正方形的6的顶点。这个可以反推证明,如果右边这2个正方形内有7个点与p点距离小于δ,例如q点,则q点与下面正方形的四个顶点距离小于δ,则和δ为SL和SR中的最小点对距离相矛盾。因此对于SL虚框中的p点,不需求出p点和右边虚线框内所有点距离,只需计算SR中与p点y坐标距离最近的6个点,就可以求出最近点对,节省了比较次数。
(否则的话,最坏情形下,在SR虚框中有可能会有n/2个点,对于SL虚框中的p点,每次要比较n/2次,浪费了算法的效率)
代码描述:
1)对点集S的点x坐标和y坐标进行升序排序,获得点集Sx和Sy
2)令δ=∞; //δ为最小点位距离
3)Divide_conquer(Sx,Sy,δ) //分治法
if (Sx.count=1) then δ=∞; //如果Sx中只有一个点,则δ=∞
return δ;
else if(Sx.count=2 and d(Sx.[0],Sx.[1])<δ) //如果Sx中只有2个点,则δ为两点之间距离
δ=d(Sx.[0],)Sx.[1]);
return δ;
else //如果Sx中多于2个点,则将Sx,Sy分治,以中心点画线,将Sx分为左右两部分SxL和SxR,Sy分为SyL和SyR
j1=1,j2=1,k1=1,k2=1;
mid = Sx.count/2; //mid为Sx中的中间点点号
L = Sx.[mid].x; //L为Sx中的中间点x坐标
for(i=1,i<Sx.count,i++)
{
if(i<=mid) //将Sx中间线以左地方的点存入到SxL,新数组保持原来的升序性质
SxL[k1] = Sx[i] k1++;
else //将Sx中间线以右的地方的点存入到SxR,新数组保持原来的升序性质
SxR.count[k2] = Sx[i] k2++;
if(Sy[i].x <L) //将Sy中间线以左地方的点存入到SyL,新数组保持原来的升序性质
SyL[j1] = Sx[i] j1++;
else //将Sy中间线以右地方的点存入到SyR,新数组保持原来的升序性质
SyR[j2] = Sx[i] j2++;
}
δL = Divide_conquer(SxL,SyL,δ); //获取Sx中的的最小点位距离δL
δR = Divide_conquer(SxR,SyR,δ); //获取Sy中的的最小点位距离δR
δ= min (δL,δR);
δ=merge(SyL,SyR,δ); //获Sx中Sy交界处的最小点位距离,并综合 δL和δR 求出点集的最小点位距离δ
return δ;
函数merge(SyL,SyR,δ)
merge(SyL,SyR,δ)
{
i1=1,i2=1;
for(i=1,i<SyL.count,i++) //获取SyL中在左边虚框(距离小于δ)内的点,存入到S'yL中,新数组保持原来的升序性质
{
if(SyL[i].x>L-δ)
then S'yL[i1]= SyL[i], i1++,
}
for(i=1,i<SyR.count,i++) //获取SyR中在右边虚框(距离小于δ)内的点,存入到S'yR中,新数组保持原来的升序性质
{
if(SyR[i].x<L+δ)
then S'yR[i2]= SyR[i], i2++,
}
t=1;
for(i=1,i<S'yL.count,i++)
{
while(S'yR[t].y< S'yL[t].y and t < SyR.count) //获取点集S'yR内距离点S'yL[t]y坐标最接近的点号
{ t++; }
for( j= max(1,t-3), j<=min(t+3,S'yR.count),j++) //计算S'yR中的点与S'yL[t]y坐标相邻的六个点的距离
{
if(d(S'yL[i],S'yL[j])<δ) //如果前两点之间距离小于δ
then δ = d(S'yL[i],S'yL[j]); //则最小点位距离δ为当前两点之间距离
}
return δ
}
3)算法时间复杂度:
首先对点集S的点x坐标和y坐标进行升序排序,需要循环2nlogn次,复杂度为O(2nlogn)
接下来在分治过程中,对于每个S’yL中的点,都需要与S’yR中的6个点进行比较
O(n)= 2O(n/2) + (n/2)*6 (一个点集划分为左右两个点集,时间复杂度为左右两个点集加上中间区域运算之和)
其解为O(n)< O(3nlogn)
因此总的时间复杂度为O(3nlogn),比蛮力法的O(n2)要高效。
总结:先由一维坐标的情况可知,在一维坐标中求n个点的最近点对的时候,是采用线性扫描的方法把x轴上的点都遍历一遍就行了,但是这不能用于二维的情况,但是也有借鉴的地方,那就一维的时间复杂度,所以这就要求能找到一种算法满足在二维的情况下时间复杂度仍然在O(nlogn),这就需要用到分治的思想了。
 图1 一维情形的分治法
图1 一维情形的分治法
 图2 距直线l的距离小于δ的所有点
图2 距直线l的距离小于δ的所有点
 图3 包含点q的δ×2δ的矩形R
图3 包含点q的δ×2δ的矩形R
 图4 矩形R中点的稀疏性
图4 矩形R中点的稀疏性
首先要找到s中所有点的x坐标的中位数并把它设为m,并把m当做将s分为s1和s2的一个分割点,并且对于在s1和s2中的点要满足各有大概n/2个,然后用分治法求出s1中的最小最近点对d1和s2的d2,
设d=min(d1,d2),如果存在一点在s1中的p3而另外一点在s2中的q3使得这两点的距离 d3小于d那么s中的最近点对就是这两点了,且p3小于m,q3大于m,距离为d3。而分治的最重要最难的地方就是把分开后的s1和s2合并的问题,由一维的情况可知对于(m-d,m] 的范围内如果存在点的话,当且仅当只能存在一点,因为要满足最短距离为d3,如果存在两点或两点以上的话就不满足了,同理在[m,m+d)中也当且仅当存在一点,但是放到二维的情况下怎么办呢?
二维的情形则要复杂些,如图2,此时,P1中所有点与P2中所有点构成的点对均为最接近点对的候选者。在最坏情况下有n2/4对这样的候选者。但是P1和P2中的点具有以下的稀疏性质,它使我们不必检查所有这n2/4对候选者。考虑P1中任意一点p,它若与P2中的点q构成最接近点对的候选者,则必有d(p,q)小于d。满足这个条件的P2中的点有多少个呢?容易看出这样的点一定落在一个d×2d的矩形R中,如图3所示。
由d的意义可知P2中任何2个S中的点的距离都不小于d。由此可以推出矩形R中最多只有6个S中的点。事实上,我们可以将矩形R的长为2d的边3等分,将它的长为d的边2等分,由此导出6个(d/2)×(2d/3)的矩形。如图4(a)所示。
若矩形R中有多于6个S中的点,则由鸽舍原理易知至少有一个d×2d的小矩形中有2个以上S中的点。设u,v是这样2个点,它们位于同一小矩形中,则
因 此 d ( u , v) ≤ 5d / 6 < d 。这 与 d 的 意义 相 矛 盾 。 也 就 是 说 矩 形 R 中 最 多 只 有 6 个 S 中 的 点 。 图 4 (b) 是 矩 形 R 中 含 有 S 中 的 6 个 点 的 极 端 情 形 。 由 于 这 种 稀 疏 性 质 , 对 于 P1 中 任 一 点 p , P2 中最 多 只 有 6 个 点 与 它 构 成 最 接 近 点 对 的 候 选 者 。 因 此 , 在 分 治 法 的 合 并 步 骤 中 , 我 们 最 多 只 需 要 检 查 6×n/2=3n 对 候 选 者 ,而 不 是 n2/4 对 候 选 者 。这 是 否 就 意味 着 我 们 可 以 在 O ( n ) 时 间 内 完 成 分 治 法 的 合并 步 骤 呢 ? 现 在 还 不 能 作 出 这 个 结 论 , 因 为 我 们 只 知 道 对 于 P1 中 每 个 S1 中 的 点 p 最 多 只 需 要 检 查 P2 中 的 6 个 点 , 但 是 我 们 并 不 确 切 地 知 道 要 检 查 哪 6 个 点 。 为 了 解 决 这 个 问 题 , 我 们 可 以 将 p 和 P2 中 所 有 S2 的 点 投 影 到 垂 直 线 l 上。 由 于 能 与 p 点 一 起 构 成 最 接 近 点 对 候 选 者 的 S2 中 点 一 定 在 矩 形 R 中 , 所 以 它 们 在 直 线 l 上 的 投 影 点 距 p 在 l 上 投 影 点 的 距 离 小 于δ 。由 上 面 的 分 析 可 知 ,这 种 投 影 点 最 多 只 有 6 个 。 因 此 , 若 将 P1 和 P2 中 所 有 S 的 点 按 其 y 坐 标 排 好 序 , 则 对 P1 中 所 有 点 p , 对 排 好 序 的 点 列 作 一 次 扫 描 , 就 可 以 找 出 所 有 最 接 近 点 对 的 候 选 者 , 对 P1 中 每 一 点 最 多 只 要 检 查 P2 中 排 好 序 的 相 继 6 个 点。
附加一到hdu的题(hdu1007)
Quoit Design
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 52710 Accepted Submission(s): 13903
Problem Description
Have you ever played quoit in a playground? Quoit is a game in which flat rings are pitched at some toys, with all the toys encircled awarded.
In the field of Cyberground, the position of each toy is fixed, and the ring is carefully designed so it can only encircle one toy at a time. On the other hand, to make the game look more attractive, the ring is designed to have the largest radius. Given a configuration of the field, you are supposed to find the radius of such a ring.
Assume that all the toys are points on a plane. A point is encircled by the ring if the distance between the point and the center of the ring is strictly less than the radius of the ring. If two toys are placed at the same point, the radius of the ring is considered to be 0.
Input
The input consists of several test cases. For each case, the first line contains an integer N (2 <= N <= 100,000), the total number of toys in the field. Then N lines follow, each contains a pair of (x, y) which are the coordinates of a toy. The input is terminated by N = 0.
Output
For each test case, print in one line the radius of the ring required by the Cyberground manager, accurate up to 2 decimal places.
Sample Input
2
0 0
1 1
2
1 1
1 1
3
-1.5 0
0 0
0 1.5
0
Sample Output
0.71
0.00
0.75
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<vector>
#include<math.h>
#include<cstdio>
#include<sstream>
#include<numeric>//STL数值算法头文件
#include<stdlib.h>
#include <ctype.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<functional>//模板类头文件
using namespace std;
typedef long long ll;
const int maxn=10005;
//const int INF=0x3f3f3f3f;
const double INF = 1e20;
const int N = 100005;
int n;
int tmpt[N];
struct Point
{
double x;
double y;
} point[N];
bool cmp(const Point& a, const Point& b)
{
if(a.x != b.x)
return a.x < b.x;
return a.y < b.y;
}
bool cmpy(const int& a, const int& b)
{
return point[a].y < point[b].y;
}
double min(double a, double b)
{
return a < b ? a : b;
}
double dis(int i, int j)
{
return sqrt((point[i].x-point[j].x)*(point[i].x-point[j].x)
+ (point[i].y-point[j].y)*(point[i].y-point[j].y));
}
double Closest_Pair(int left, int right)
{
double d = INF;
if(left==right)
return d;
if(left + 1 == right)
return dis(left, right);
int mid = (left+right)>>1;
double d1 = Closest_Pair(left,mid);
double d2 = Closest_Pair(mid+1,right);
d = min(d1,d2);
int i,j,k=0;
//分离出宽度为d的区间
for(i = left; i <= right; i++)
{
if(fabs(point[mid].x-point[i].x) <= d)
tmpt[k++] = i;
}
sort(tmpt,tmpt+k,cmpy);
//线性扫描
for(i = 0; i < k; i++)
{
for(j = i+1; j < k && point[tmpt[j]].y-point[tmpt[i]].y<d; j++)
{
double d3 = dis(tmpt[i],tmpt[j]);
if(d > d3)
d = d3;
}
}
return d;
}
int main()
{
while(~scanf("%d",&n)&&n)
{
for(int i = 0; i < n; i++)
scanf("%lf %lf",&point[i].x,&point[i].y);
sort(point,point+n,cmp);
printf("%.2lf\n",Closest_Pair(0,n-1)/2);
}
return 0;
}






