训练/验证/测试集设置;偏差/方差;high bias/variance;正则化;为什么正则化可以减小过拟合
1. 训练、验证、测试集
对于一个需要解决的问题的样本数据，在建立模型的过程中，我们会将问题的data划分为以下几个部分：
- 训练集（train set）：用训练集对算法或模型进行训练过程；
- 验证集（development set）：利用验证集或者又称为简单交叉验证集（hold-out cross validation set）进行交叉验证，选择出最好的模型；
- 测试集（test set）：最后利用测试集对模型进行测试，获取模型运行的无偏估计。
小数据时代
在小数据量的时代，如：100、1000、10000的数据量大小，可以将data做以下划分：
无验证集的情况：70% / 30%；
有验证集的情况：60% / 20% / 20%；
通常在小数据量时代，以上比例的划分是非常合理的。
大数据时代
但是在如今的大数据时代，对于一个问题，我们拥有的data的数量可能是百万级别的，所以验证集和测试集所占的比重会趋向于变得更小。
验证集的目的是为了验证不同的算法哪种更加有效，所以验证集只要足够大能够验证大约2-10种算法哪种更好就足够了，不需要使用20%的数据作为验证集。如百万数据中抽取1万的数据作为验证集就可以了。
测试集的主要目的是评估模型的效果，如在单个分类器中，往往在百万级别的数据中，我们选择其中1000条数据足以评估单个模型的效果。
- 100万数据量：98% / 1% / 1%；
- 超百万数据量：99.5% / 0.25% / 0.25%（或者99.5% / 0.4% / 0.1%）
Notation
建议验证集要和训练集来自于同一个分布，可以使得机器学习算法变得更快；
如果不需要用无偏估计来评估模型的性能，则可以不需要测试集。
2. 偏差、方差
对于下图中两个类别分类边界的分割：
从图中我们可以看出，在欠拟合（underfitting）的情况下，出现高偏差（high bias）的情况；在过拟合（overfitting）的情况下，出现高方差（high variance）的情况。
在bias-variance tradeoff 的角度来讲，我们利用训练集对模型进行训练就是为了使得模型在train集上使 bias 最小化，避免出现underfitting的情况；
但是如果模型设置的太复杂，虽然在train集上 bias 的值非常小，模型甚至可以将所有的数据点正确分类，但是当将训练好的模型应用在dev 集上的时候，却出现了较高的错误率。这是因为模型设置的太复杂则没有排除一些train集数据中的噪声，使得模型出现overfitting的情况，在dev 集上出现高 variance 的现象。
所以对于bias和variance的权衡问题，对于模型来说是一个十分重要的问题。
例子：
几种不同的情况：
以上为在人眼判别误差在0%的情况下，该最优误差通常也称为“贝叶斯误差”，如果“贝叶斯误差”大约为15%，那么图中第二种情况就是一种比较好的情况。
High bias and high variance的情况
上图中第三种bias和variance的情况出现的可能如下：
没有找到边界线，但却在部分数据点上出现了过拟合，则会导致这种高偏差和高方差的情况。
虽然在这里二维的情况下可能看起来较为奇怪，出现的可能性比较低；但是在高维的情况下，出现这种情况就成为可能。
3. 机器学习的基本方法
在训练机器学习模型的过程中，解决High bias 和High variance 的过程：
- 1.是否存在High bias ?
增加网络结构，如增加隐藏层数目；
训练更长时间；
寻找合适的网络架构，使用更大的NN结构；- 2.是否存在High variance？
获取更多的数据；
正则化（ regularization）；
寻找合适的网络结构；
在大数据时代，深度学习对监督式学习大有裨益，使得我们不用像以前一样太过关注如何平衡偏差和方差的权衡问题，通过以上方法可以使得再不增加另一方的情况下减少一方的值。
4. 正则化（regularization）
利用正则化来解决High variance 的问题，正则化是在 Cost function 中加入一项正则化项，惩罚模型的复杂度。
Logistic regression
5. 为什么正则化可以减小过拟合
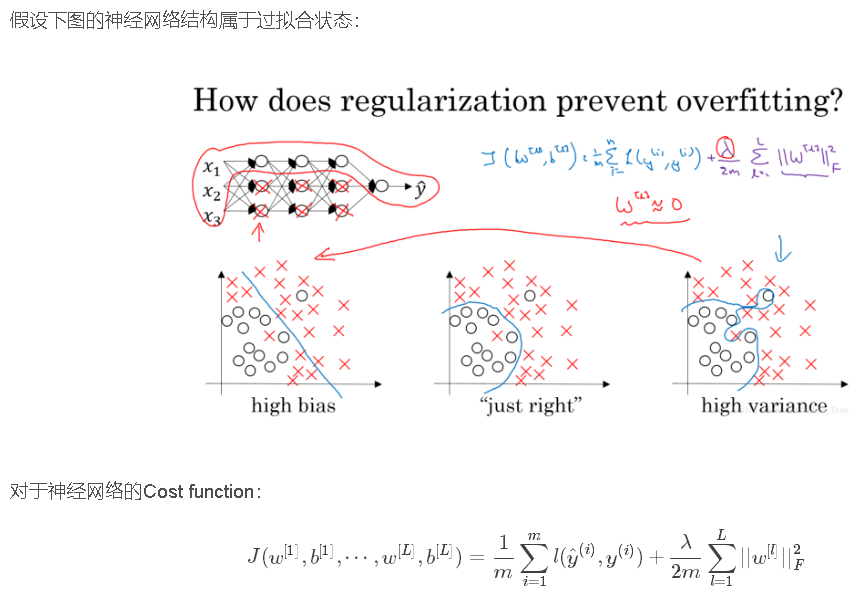
加入正则化项，直观上理解，正则化因子λ设置的足够大的情况下，为了使代价函数最小化，权重矩阵W就会被设置为接近于0的值。则相当于消除了很多神经元的影响，那么图中的大的神经网络就会变成一个较小的网络。
当然上面这种解释是一种直观上的理解，但是实际上隐藏层的神经元依然存在，但是他们的影响变小了，便不会导致过拟合。
数学解释
