激活函数总结

一、激活函数

1.什么是激活函数

激活函数: 就是在神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。

2.为什么要有激活函数

如果不用激活函数，每一层的输出都是上一层的线性组合，从而导致整个神经网络的输出为神经网络输入的线性组合，无法逼近任意函数。

3.激活函数的特性

非线性
可微性：当优化方法是基于梯度时，此性质是必须的
单调性：当激活函数是单调时，可保证单层网络是凸函数
输出值的范围：当激活函数输出值是有限的时候，基于梯度的优化方法会更加稳定，因为特征的表示受有限权值的影响更显著；当激活函数的输出是无限时，模型的训练会更加高效，不过在这种情况小，一般需要更小的Learning Rate.

二、Sigmoid/tanh/softmax

1.sigmoid

　　Sigmoid函数的表达式为

　　导数为：

$y = 1$

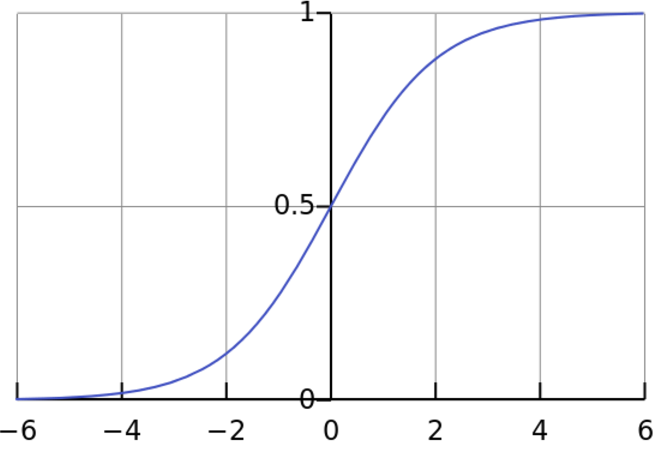
　　Sigmoid函数是传统神经网络中最常用的激活函数，一度被视为神经网络的核心所在。

　　从数学上来看，Sigmoid函数对中央区的信号增益较大，对两侧区的信号增益小，在信号的特征空间映射上，有很好的效果。从神经科学上来看，中央区酷似神经元的兴奋态，两侧区酷似神经元的抑制态，因而在神经网络学习方面，可以将重点特征推向中央区，将非重点特征推向两侧区。

对比sigmoid类函数主要变化是：
　　1）单侧抑制
　　2）相对宽阔的兴奋边界
　　3）稀疏激活性

Sigmoid 和 Softmax 区别：

　　sigmoid将一个real value映射到（0,1）的区间，用来做二分类。而 softmax 把一个 k 维的real value向量（a1,a2,a3,a4….）映射成一个（b1,b2,b3,b4….）其中 bi 是一个 0～1 的常数，输出神经元之和为 1.0，所以相当于概率值，然后可以根据 bi 的概率大小来进行多分类的任务。二分类问题时 sigmoid 和 softmax 是一样的，求的都是 cross entropy loss，而 softmax 可以用于多分类问题多个logistic回归通过叠加也同样可以实现多分类的效果，但是 softmax回归进行的多分类，类与类之间是互斥的，即一个输入只能被归为一类；多个logistic回归进行多分类，输出的类别并不是互斥的，即"苹果"这个词语既属于"水果"类也属于"3C"类别。

2.TanHyperbolic（tanh）

　　TanHyperbolic(tanh)函数又称作双曲正切函数，数学表达式为

　　导数为：

　　图像为：

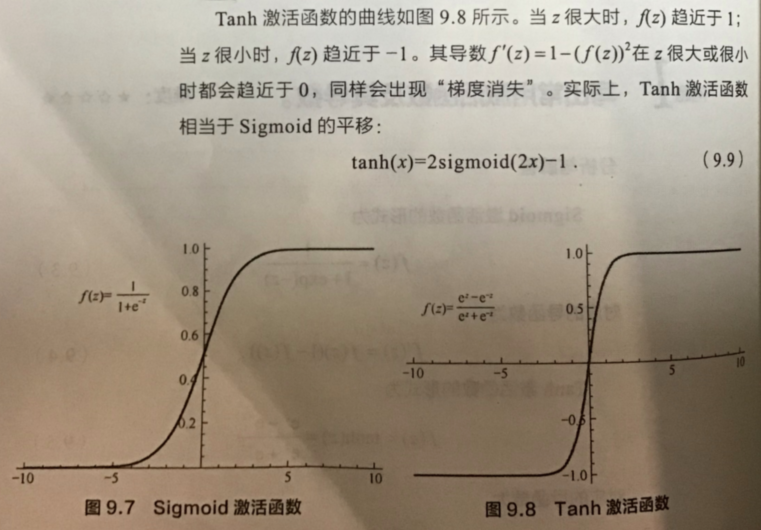
　　在具体应用中，tanh函数相比于Sigmoid函数往往更具有优越性，这主要是因为Sigmoid函数在输入处于[-1,1]之间时，函数值变化敏感，一旦接近或者超出区间就失去敏感性，处于饱和状态，影响神经网络预测的精度值。而tanh的输出和输入能够保持非线性单调上升和下降关系，符合BP网络的梯度求解，容错性好，有界，渐进于0、1，符合人脑神经饱和的规律，但比sigmoid函数延迟了饱和期.tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。与 sigmoid 的区别是，tanh 是 0 均值的，因此实际应用中 tanh 会比 sigmoid 更好。

3.softmax

　　Sigmoid函数如果用来分类的话，只能进行二分类，而这里的softmax函数可以看做是Sigmoid函数的一般化，可以进行多分类。softmax函数的函数表达式为：

　　二分类和多分类其实没有多少区别。用的公式仍然是y=wx + b。但有一个非常大的区别是他们用的激活函数是不同的。逻辑回归用的是sigmoid，这个激活函数的除了给函数增加非线性之外还会把最后的预测值转换成在【0,1】中的数据值。也就是预测值是0<y<1。我们可以把最后的这个预测值当做是一个预测为正例的概率。在进行模型应用的时候我们会设置一个阈值，当预测值大于这个阈值的时候，我们判定为正例子，反之我们判断为负例。这样我们可以很好的进行二分类问题。而多分类中我们用的激活函数是softmax。为了能够比较好的解释它，我们来说一个例子。假设我们有一个图片识别的4分类的场景。我们想从图片中识别毛，狗，鸡和其他这4种类别。那么我们的神经网络就变成下面这个样子的。

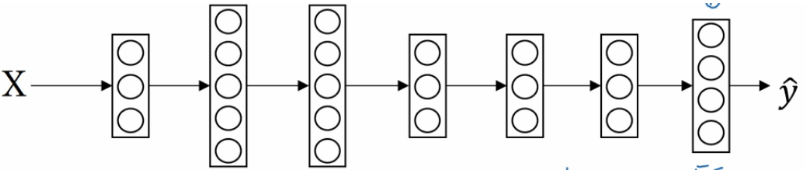
　　我们最后的一层中使用的激活函数就是softmax。我们发现跟二分类在输出层之后一个单元不同的是，使用softmax的输出层拥有多个单元，实际上我们有多少个分类就会有多少个单元，在这个例子中，我们有4个分类，所以也就有4个神经单元，它们代表了这4个分类。在softmax的作用下每个神经单元都会计算出当前样本属于本类的概率。如下：

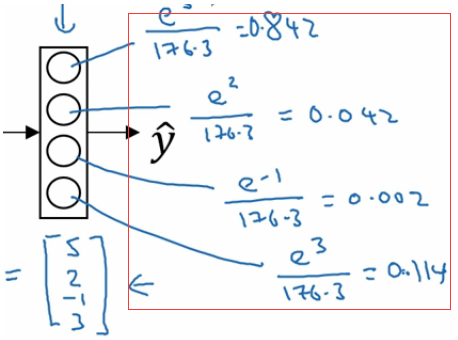
　　如上图，该样本属于第一个分类的概率是0.842，属于第二个分类的概率是0.042，属于第三个分类的概率是0.002，属于第四个分类的概率是0.114. 我们发现这些值相加等于一，因为这些值也是经过归一化的结果。整个效果图可以参考下面的例子，这是一个比较直观的图。

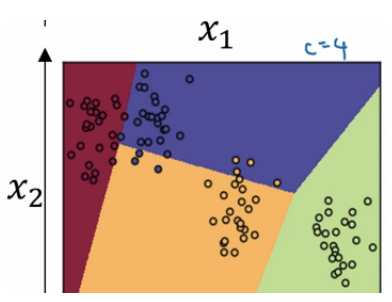
Softmax的损失函数

　　既然softmax的输出变成了多个值，那么我们如何计算它的损失函数呢，有了损失函数我们才能进行梯度下降迭代并根据前向传播和反向传播进行学习。如下图：

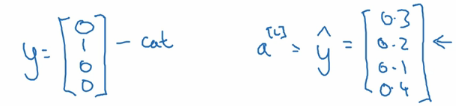
　　还是假设有4个分类，那么实际的预测向量，也会有4个维度。如上图左边的样子。如果是属于第二个分类，那么第二个值就是1，其他值都是0。假设右边的向量是预测值，每个分类都有一个预测概率。那么我们的损失函数就是。

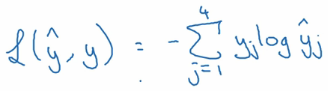
　　由于实际值得向量只有一个是1，其他的都是0. 所以其实到了最后的函数是下面这个样子的

　　有了损失函数，我们就可以跟以前做逻辑回归一样做梯度下降就可以了。

softmax的梯度求解

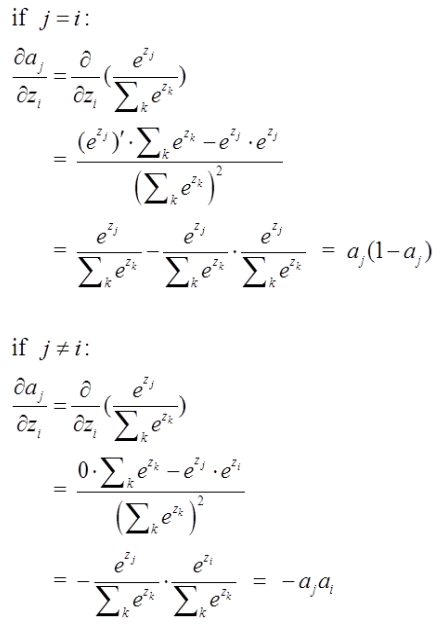
三、ReLu/softplus/GeLu

1.Relu

　　ReLu函数的全称为Rectified Linear Units

　　函数表达式为： $y = m a x$

　　导数为：

$y = m a x$

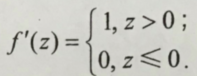
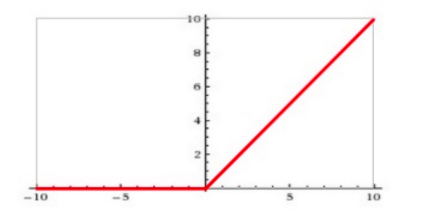
Sigmoid ，tanh与ReLU 比较：

　　sigmoid，tanh 会出现梯度消失问题，ReLU 的导数就不存在这样的问题。

优点：

（1）从计算的角度上，Sigmoid和Tanh激活函数均需要计算指数，复杂度高，而ReLU只需要一个阈值即可得到激活值；

（2）ReLU的非饱和性溃疡有效地解决梯度消失的问题，提供相对宽的激活边界；

（3）ReLU的单侧抑制提供了网络的稀疏表达能力

缺点：

训练过程中会导致神经元死亡的问题。这是由于函数f(z)=max(0,z)导致负梯度在经过该ReLU单元时被置为0，且在之后也不被任何数据激活，即流经该神经元的梯度永远为0，不对任何数据产生响应。

在实际训练中，如果学习率设置较大，会导致一定比例的神经元不可逆死亡，进而参数梯度无法更新，整个训练过程失败。

2.softplus

$y = m a x$

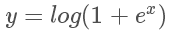
　　ReLu和softplus的函数曲线如下：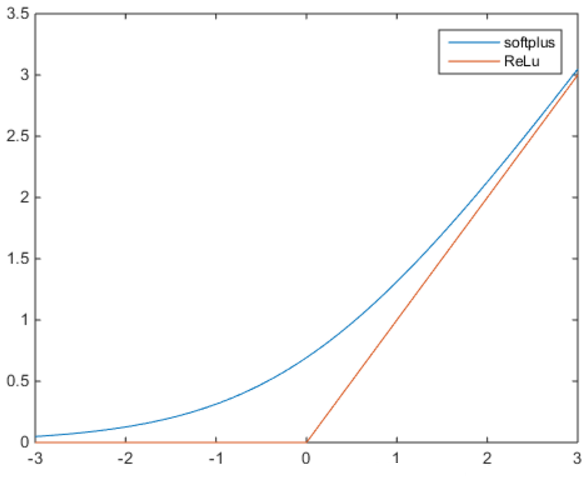

可以看到，softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型，

而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。

softplus和ReLu相比于Sigmoid的优点在哪里呢？

采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。
Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生（以及一些人的生物解释balabala）。

3.GeLu

出自论文：GAUSSIAN ERROR LINEAR UNITS(GELUS)

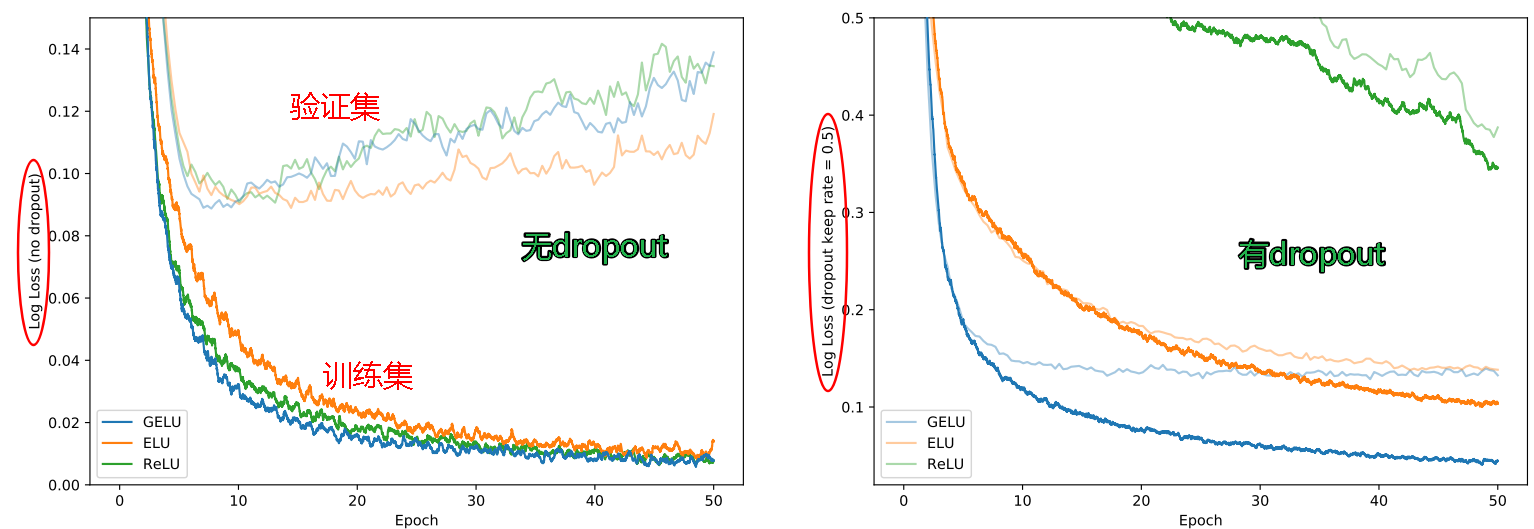
动机：在神经网络的建模过程中，模型很重要的性质就是非线性，同时为了模型泛化能力，需要加入随机正则，例如dropout(随机置一些输出为0,其实也是一种变相的随机非线性激活)，而随机正则与非线性激活是分开的两个事情，而其实模型的输入是由非线性激活与随机正则两者共同决定的。GELUs正是在激活中引入了随机正则的思想，是一种对神经元输入的概率描述，直观上更符合自然的认识。

GeLu公式：

GeLu的近似函数：

GeLu的函数曲线：

GeLu的源码：

def gelu(x):
  """Gaussian Error Linear Unit.

  This is a smoother version of the RELU.
  Original paper: https://arxiv.org/abs/1606.08415
  Args:
    x: float Tensor to perform activation.

  Returns:
    `x` with the GELU activation applied.
  """
  cdf = 0.5 * (1.0 + tf.tanh(
      (np.sqrt(2 / np.pi) * (x + 0.044715 * tf.pow(x, 3)))))
  return x * cdf

参考文献：

【1】softmax的log似然代价函数（公式求导）

【2】深度学习----BP+SGD+激活函数+代价函数+基本问题处理思路 - 郭大侠写leetcode - CSDN博客

【3】GELU 激活函数

posted @ 2018-07-07 09:42 nxf_rabbit75 阅读(10842) 评论(0) 编辑收藏举报

刷新页面返回顶部