线性回归
1.标准回归
1 from numpy import * 2 import matplotlib.pyplot as plt 3 4 #标准回归函数和数据导入函数 5 def loadDataSet(filename): 6 # f = open(filename) 7 # dataSet = [] 8 # data=f.readlines() 9 # for line in data: 10 # line=line.strip().split('\t') 11 # dataSet.append(line) 12 # print(dataSet) 13 numFeat = len(open(filename).readline().split('\t'))-1 14 dataMat = [] 15 labelMat = [] 16 f = open(filename) 17 for line in f.readlines(): 18 lineArr = [] 19 curline = line.strip().split('\t') 20 for i in range(numFeat): 21 lineArr.append(float(curline[i])) 22 labelMat.append(float(line.strip().split('\t')[-1])) 23 dataMat.append(lineArr) 24 return dataMat,labelMat 25 # print("dataMat",dataMat) 26 # print("labelMat",labelMat) 27 28 #计算回归系数 29 def standRegres(xArr,yArr): 30 xMat = mat(xArr) 31 yMat = mat(yArr).T 32 xTx = xMat.T*xMat 33 if linalg.det(xTx) == 0.0: 34 print("该矩阵是奇异矩阵，不能求逆矩阵") 35 return 36 ws = xTx.I * (xMat.T * yMat)#回归系数 37 return ws 38 39 #绘标准回归 40 def fig_regre(xMat,yMat,ws): 41 fig = plt.figure() 42 ax = fig.add_subplot(111) 43 ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0])#flatten用于array和mat对象，flatten是深拷贝，不改变 44 #xMat[:,1].flatten()==>matrix[[]] xMat[:,1].flatten().A==>array[[]] xMat[:,1].flatten().A[0]==>array[] 45 #plt.show() 46 47 xCopy = xMat.copy()#浅拷贝，改变 48 xCopy.sort(0) 49 #print(xCopy.sort(0)) 50 print("ws",ws) 51 yHat = xCopy * ws 52 ax.plot(xCopy[:,1],yHat,c='r') 53 plt.show()
2.局部加权线性回归
局部加权回归是基于非参数学习算法的思想，使得特征的选择更好。赋予预测点附近每一个点以一定的权值，在这上面基于波长函数来进行普通的线性回归.可以实现对临近点的精确拟合同时忽略那些距离较远的点的贡献，即近点的权值大，远点的权值小，k为波长参数，控制了权值随距离下降的速度，越大下降的越快。越小越精确并且太小可能出现过拟合的问题。
(红色地方加上W权重，W跟距离有关，距离越近，权重越大)
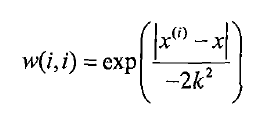
1 #局部加权线性回归函数 2 def lwlr(testPoint,xArr,yArr,k=1.0): 3 #创建对角矩阵 4 xMat = mat(xArr) 5 yMat = mat(yArr).T 6 m = list(shape(xMat))[0] 7 weights = mat(eye(m)) 8 9 #权重值大小以指数级衰减 10 for j in range(m): 11 diffMat = testPoint - xMat[j,:] 12 weights[j,j] = exp(diffMat*diffMat.T/(-2.0 * k**2)) 13 # weights[j, j] = exp (linalg.det(diffMat) / (-2.0 * k ** 2)) 14 xTx = xMat.T * (weights * xMat) 15 if linalg.det(xTx) == 0: 16 print("非奇异，不能求逆") 17 ws = xTx.I * (xMat.T * (weights * yMat)) 18 return testPoint * ws 19 20 #测试,得到y的估计值 21 def lwlrText(testArr,xArr,yArr,k=1.0): 22 m = list(shape(testArr))[0] 23 yHat = zeros(m) 24 for i in range(m): 25 yHat[i] = lwlr(testArr[i],xArr,yArr,k) 26 return yHat
测试
1 if __name__ == '__main__': 2 xArr1, yArr1 = loadDataSet("ex0.txt") 3 # ws1 = standRegres(xArr1,yArr1) 4 xMat = mat(xArr1) 5 yMat = mat(yArr1) 6 # yHat1 = xMat1 * ws1#估测值 7 #fig_regre(xMat1, yMat1, ws1) 8 # p1 = corrcoef(yHat1.T, yMat1) 9 yHat1 = lwlrText (xArr1, xArr1, yArr1, k=1.0) 10 yHat2 = lwlrText (xArr1, xArr1, yArr1, k=0.01) 11 yHat3 = lwlrText (xArr1, xArr1, yArr1, k=0.003) 12 13 strInd = xMat[:, 1].argsort (0) # argsort函数返回的是数组值从小到大的索引值 14 xSort = xMat[strInd][:, 0, :] 15 16 fig = plt.figure () 17 ax = fig.add_subplot(221) 18 ax.plot (xSort[:, 1], yHat1[strInd]) 19 ax.scatter (xMat[:, 1].flatten ().A[0], yMat.T.flatten ().A[0], s=2, c='blue') 20 21 ax = fig.add_subplot (222) 22 ax.plot (xSort[:, 1], yHat2[strInd]) 23 ax.scatter (xMat[:, 1].flatten ().A[0], yMat.T.flatten ().A[0], s=2, c='green') 24 25 ax = fig.add_subplot (223) 26 ax.plot (xSort[:, 1], yHat3[strInd]) 27 ax.scatter (xMat[:, 1].flatten ().A[0], yMat.T.flatten ().A[0], s=2, c='red') 28 plt.show () 29 # xArr2, yArr2 = loadDataSet ("ex1.txt") 30 # ws2 = standRegres (xArr2, yArr2) 31 # xMat2 = mat (xArr2) 32 # yMat2 = mat (yArr2) 33 # yHat2 = xMat2 * ws2 # 估测值 34 #fig_regre (xMat2, yMat2, ws2) 35 # p2 = corrcoef (yHat2.T, yMat2)#计算预测值和真实值之间的相关性 36 # print ("p2", p2)
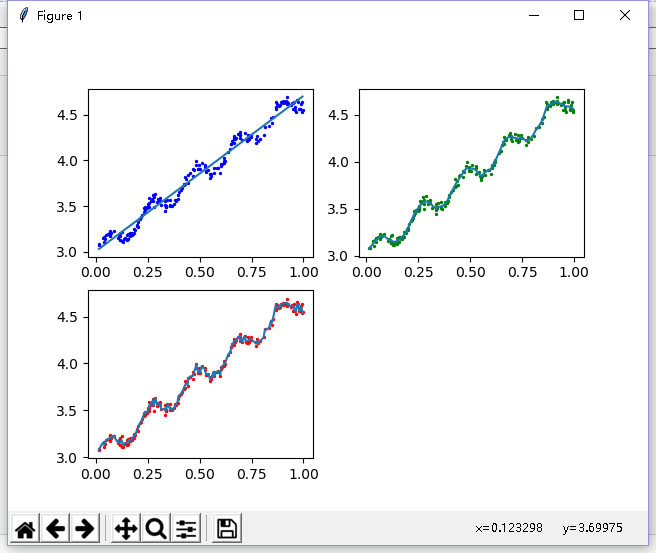
结果如下：图1 欠拟合 k=1.0 与最小二乘法差不多，
图2 k=0.001 可以挖出数据的潜在规律
图3 k=0.003 过拟合
