CART)

总览

算法	功能	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益比	支持	支持	支持
CART	分类/回归	二叉树	基尼系数,均方差	支持	支持	支持

论文链接：
- ID3：https://link.springer.com/content/pdf/10.1007%2FBF00116251.pdf　　
- C4.5：https://link.springer.com/content/pdf/10.1007%2FBF00993309.pdf
sklearn库： https://www.studyai.cn/modules/tree.html
- 每个样本的输出概率prob：对于一个叶子节点，该叶子节点预测类别对应的训练样本数占该叶子节点所有训练样本数的比例。
决策树可视化：https://www.cnblogs.com/pinard/p/6056319.html

1.ID3（分类）

信息熵：随机变量不确定性的度量

$$H(D) = -\sum\limits_{k=1}^{K}\frac{|C_k|}{|D|}log_2\frac{|C_k|}{|D|}$$

条件信息熵：在特征A给定的条件下对数据集D分类的不确定性

$$H(D|A) = -\sum\limits_{i=1}^{n}\frac{|D_i|}{|D|}H(D_i)=-\sum\limits_{i=1}^{n}\frac{|D_i|}{|D|}\sum\limits_{k=1}^{K}\frac{|D_{ik}|}{|D_i|}log_2(\frac{|D_{ik}|}{|D_i|})$$

信息增益：知道特征A的信息而使类D的信息的不确定减少的程度（对称）

$$I(D,A) = H(D) - H(D|A)$$

分裂标准：寻找信息增益大的特征

缺点：

存在偏向于选择取值较多的特征问题
仅适用于类别特征，连续值不适用
没考虑缺失值处理
没考虑过拟合的问题

2.C4.5（分类）

对ID3算法的改进：

用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足$I_R(D,A) = \frac{I(A,D)}{H_A(D)}$，分母为特征熵：$H_A(D) = -\sum\limits_{i=1}^{n}\frac{|D_i|}{|D|}log_2\frac{|D_i|}{|D|}$，其中D为样本特征输出的集合，A为特征。特征数越多的特征对应的特征熵越大，它作为分母，可以校正信息增益任意偏向于取值较多的特征的问题。
连续的特征离散化，比如m个样本的连续特征A有m个，从小到大排列为$a_1,a_2,...,a_m$，则C4.5取相邻两样本值的平均值，一共取得m-1个划分点，其中第i个划分点$T_i = \frac{a_i+a_{i+1}}{2}$，对于这m-1个点，分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为$a_t$ $a_{t}$
缺失值处理：
- 在选择分裂属性的时候，训练样本存在缺失值，如何处理？
  - 对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分，对每个样本设置一个权重（初始可以都为1），然后划分数据，一部分是有特征值A的数据D1，另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比，最后乘上一个系数，这个系数是无特征A缺失的样本加权后所占加权总样本的比例。
- 分类属性选择完成，对训练样本分类，发现属性缺失怎么办？
  - 可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1,A2,A3。 3个特征值对应的无缺失A特征的样本个数为2,3,4.则a同时划分入A1，A2，A3。对应权重调节为2/9,3/9, 4/9。
在树构造过程中进行剪枝；

缺点：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

3.CART（分类/回归）

（1）分类

假设有K个类别，第k个类别的概率为$p_k$

$$Gini(p) = \sum\limits_{k=1}^{K}p_k(1-p_k) = 1- \sum\limits_{k=1}^{K}p_k^2$$

如果K=2，则基尼系数为：

$$Gini(p) = 2p(1-p)$$

样本D的基尼系数：

$$Gini(D) = 1-\sum\limits_{k=1}^{K}(\frac{|C_k|}{|D|})^2$$

对于样本D，如果根据特征A的某个值，把D分成D1和D2，则在特征A的条件下，D的基尼系数为：

$$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$$

连续特征处理：

对于CART分类树连续值的处理问题，其思想和C4.5是相同的，都是将连续的特征离散化。唯一的区别在于在选择划分点时的度量方式不同，C4.5使用的是信息增益比，则CART分类树使用的是基尼系数。要注意的是，与ID3或者C4.5处理离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。具体参考

离散特征处理：

二分离散
在ID3或者C4.5中，如果某个特征A被选取建立决策树节点，如果它有A1,A2,A3三种类别，我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同，他采用的是不停的二分，还是这个例子，CART分类树会考虑把A分成 ${A 1} 和 {A 2, A 3}$

分类树建立过程：参考链接

（2）回归

除了概念的不同，CART回归树和CART分类树的建立和预测的区别主要有下面两点：

连续值的处理方法不同，回归使用均方差最小

　　　对于任意划分特征A，对应的任意划分点s两边划分成的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小所对应的特征和特征值划分点。其中， $c_{1}$

$c_{1}$

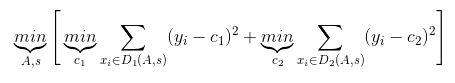
决策树建立后做预测的方式不同

（3）剪枝

step1：从原始决策树生成各种剪枝效果的决策树；
step2：用交叉验证来检验剪枝后的预测能力，选择泛化预测能力最好的剪枝后的数作为最终的CART树。

剪枝的损失函数度量，对于任意的一棵子树T：　　

其中， $α$ 为在正则化参数，$C(T_t)$为训练数据的预测误差，分类树是用基尼系数度量，回归树是均方差误差

当$\alpha=0$时，没有正则化，原始生成的CART树即为最优子树
当$\alpha=\infty$，即正则化强度达到最大，此时，由原始生成的CART树的根节点组成的单节点树为最优子树。
对于固定的$\alpha$，一定存在使损失函数$C_\alpha(T)$最小的子树。

对于任意一个内节点t的子树$T_t$：

如果没有剪枝，损失为$C_{\alpha}(T_t) = C(T_t) + \alpha |T_t|$
如果剪枝，仅仅保留根节点，则损失为$C_{\alpha}(T) = C(T) + \alpha$

$\alpha$对损失值的影响：

当$\alpha=0$或者很小时，$C_{\alpha}(T_t) < C_{\alpha}(T)$
当$\alpha$增大到一定程度，$C_{\alpha}(T_t) = C_{\alpha}(T)$
当$\alpha$继续增大，$C_{\alpha}(T_t) > C_{\alpha}(T)$

当$\alpha = \frac{C(T)-C(T_t)}{|T_t|-1}$时，$T_{t}$和T有相同的损失函数，但是T节点更少，因此可以对子树$T_t$进行剪枝，也就是将它的子节点全部剪掉，变为一个叶子节点T。可以计算出每个子树是否剪枝的阈值$\alpha$，如果我们把所有的节点是否剪枝的值αα都计算出来，然后分别针对不同的$\alpha$所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的$\alpha$，有了这个$\alpha$，我们就可以用对应的最优子树作为最终结果。

CART剪枝算法：

输入：CART生成树T
输出：最优决策子树$T_\alpha$

step1：初始化$\alpha_{min}=\infty$ $α_{m i n} = \infty$

step2：自下而上计算各内部节点t的训练误差损失函数$C_{\alpha}(T_t)$（回归树为均方差，分类树为基尼系数），叶子节点数$T_{t}$，以及正则化阈值$\alpha= min\{\frac{C(T)-C(T_t)}{|T_t|-1}, \alpha_{min}\}$，更新$\alpha_{min}=\alpha$

step3：得到所有节点的$\alpha$值的集合M

step4：从M中选择最大的$\alpha_{k}$，自上而下的访问子树t的内部节点，如果$\frac{C(T)-C(T_t)}{|T_t|-1} \leq \alpha_k$时，进行剪枝。并决定叶节点t的值，如果是分类树，则是概率最高的类别，如果是回归树，则是所有样本输出的均值，这样得到$\alpha_k$对应的最优子树$T_k$。

step5：最优子树集合$\omega=\omega \cup T_k，M= M -\{\alpha_k\}$

step6：如果M不空，则回到step4，否则就已经得到了所有的可选最优子树集合$\omega$

step7：采用交叉验证在$\omega$选择最优子树$T_{\alpha}$

4.样本不均衡

方法一：加上类别权重和样本权重，即样本数少的类别样本权重高，在sklearn中即为iclass_weight和sample_weight两个参数。

方法二：采样，即通过采样增加少数类别样本数，或者子采样选择部分多数类别样本数，以达到类别平衡。

5.决策树的优缺点

优点：

计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据（对缺失值很宽容）
非黑盒，可解释性
轻松去除无关的属性(Gain=0)
可以处理区间型变量（Interval)（训练速度视数据规模而定）
分类速度快(O(depth)，针对类别型变量和次序型变量)
对数据分布没有特别严格的要求
可以同时对付数据中线性和非线性的关系
可作为有效工具来帮助其他模型挑选自变量
使用信息原理对大样本的属性进行信息量分析，并计算各属性的信息量，找出反映类别的重要属性，可准确、高效地发现哪些属性对分类最有意义。（如区间型变量的分箱操作）

缺点：

单棵决策树分类能力弱，并且对连续值变量难以处理；
容易过拟合（后续出现了随机森林，减小了过拟合现象）；
对有时间顺序的数据，需要很多预处理的工作（连续型目标变量不太适用）；
当类别太多时，错误可能就会增加的比较快；
在处理特征关联性比较强的数据时表现得不是太好
缺乏诸如回归或聚类丰富多样的检测指标和评价方法
对training set rotation敏感，可以用pca解决或者斜决策树
对训练集数据的微小变化敏感
决策树算法对区间型自变量进行分箱操作时，无论是否考虑了顺序因素，都有可能因为分箱丧失某些重要的信息。尤其是当分箱前的区间型变量与目标变量有明显的线性关系时，这种分箱操作造成的信息损失更为明显。

参考文献：

【1】决策树算法原理(下)（刘建平大佬）

【2】分类回归树CART(上)

posted @ 2019-02-16 18:19 nxf_rabbit75 阅读(984) 评论(1) 编辑收藏举报

刷新页面返回顶部