Leetcode---8.前缀和&差分篇
一、基本概念
前缀和指一个数组的某下标之前的所有数组元素的和（包含其自身），前缀和是一种重要的预处理，能够降低算法的时间复杂度。
preSum是前缀和数组, nums是内容数组。
拥有前缀和数组后, 我们可以在O(1)的时间复杂度内求出区间和。
使用场景：
前缀和计算通常作为某种计算的预处理过程，作数据记忆以减少计算，时间复杂度为O(n)。预处理后各点的前缀和保存下来（数组或hash表），供后续计算时查询，例如从i到j的子数组的和为 S[j]−S[i−1]，即两点前缀和之差，时间复杂度为O(1)。
1.一维前缀和
涉及连续子数组求和时，通常使用“前缀和”来解决。最简单的一维前缀和如下：
前缀和为从第0项到第i项的和，即S[i]=A[0]+A[1]+…+A[i]，计算时基于前值S[i]= S[i-1] +A[i]
某项值可以表示为相邻前缀和之差：A[i]=S[i]−S[i−1]
从i到j的子数组的和：A[i]+…+A[j]=S[j]−S[i−1]
2.二维前缀和
二维矩阵（或二维数组）及前缀和示例如下
二维前缀和 S[i][j] = S[i-1][j] + S[i][j-1] – S[i-1][j-1] + A[i][j]
子矩阵(r1, c1)到(r2, c2)的和为：S[r2][c2] – S[r1-1][c2] – S[r2][c1-1] + S[r1-1][c1-1]
3.树上前缀和
树上前缀和通常分为两种：
从根到某节点的路径上点（或边）的值之和，如下图所示：
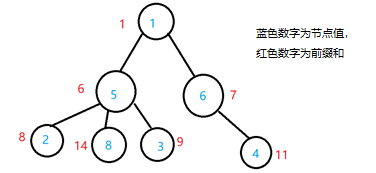
某节点及其所有子节点（或边）的值之和，如下下图：
点击查看代码
class NumArray {
// 前缀和数组
private int[] preSum;
/* 输入一个数组，构造前缀和 */
public NumArray(int[] nums) {
// preSum[0] = 0，便于计算累加和
preSum = new int[nums.length + 1];
// 计算 nums 的累加和
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
/* 查询闭区间 [left, right] 的累加和 */
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}
new 一个新的数组 preSum 出来，preSum[i] 记录 nums[0..i-1] 的累加和。如果我想求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。这样，sumRange 函数仅仅需要做一次减法运算，避免了每次进行 for 循环调用，最坏时间复杂度为常数 O(1)。
4.练习题
- 和为K的子数组
- 区间子数组个数(中等)
- 水果成篮(中等)
二、差分
1.差分数组定义
真实数组a = {a[1]、a[2]、…、a[n]} // 各点真实数据
差分数组df = {df[1]、df[2]、…、df[n]} // 各点数据的变更值
df[i] = a[i] - a[i-1] // 差分数组各点数据为真实数据的变更值
a[i] = df[1] + df[2] …+ df[i] // 差分数组的前缀和即为真实数组
a[i] = a[i-1] + df[i] // 真实数据也可以从上一点数据+变更值求出
2.差分算法解题模板（题目中给出的往往为数据变更点）
- 初始化差分数组：根据数据变更点构造差分数组，常用map<int, int> （key: 变更点， value：变更值）
- 根据差分数组求原始数组：对差分数组求前缀和，求出的即为原始数组
- 根据原始数组判断结果
使用场景：
差分算法题型特征：在一段区间内（例如时间/站点）给出数据变更点（例如上下车/占用释放等），需要感知变更后数据值。
- 一维差分：主要用于对子数组（或区间）的元素整体加减固定值，特别是子数组较多时，可提高性能。
- 二维差分：对子矩阵元素整体进行加减处理，在子矩阵较多时，为提高性能，可以考虑用差分数组来处理。
2.练习题
1094.拼车：本题为一段区间给出数据变更的点（上车/下车点+人数），需要求出变更后的数据（人数）是否满足（车容量），典型的差分算法特征，根据变更数据采用map构造差分数组，差分数组求前缀和还原各时间点真实数据，判断真实人数是否满足
1109.航班预订统计：经典差分问题，本题与在拼车的基础上叠加了返回值需要返回其真实数据数组，在上题基础上仅差异在结果的处理。题型关键为：一段区间（城市）给出数据变更的点（预定人数），需要求出变更后的数据（各站点人数），典型的差分算法特征
253.会议室Ⅱ：题型关键为：一段区间（时间）给出数据变更的点（会议室预定/释放），需要求出变更后的数据（会议室数量），典型的差分算法特征
参考链接：
【1】得嘞,一文把前缀和给扒的干干净净
【2】小而美的算法技巧：前缀和数组
