Leetcode---5.二分搜索篇

基本概念：
二分法属于编程五大常用算法（分治、贪心、回溯、分支定界和动态规划）中的分治算法。分治算法的思想就是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同，求出子问题的解，就可得到原问题的解。二分法由于其划分的简单和均匀的特点，是分治求解时经常采用的一种有效的方法。

二分法，也称为折半查找法，其基本原理是每次搜索可以舍弃一半，从留下的一半中寻找目标值，以此来缩小搜索范围。运用二分搜索的前提是序列必须是有序的。

使用场景：
二分法的前提是序列必须是有序的，时间复杂度是O(logN)，一般可用于对普通搜索方法的优化。其场景一般有以下几种：
（1）寻找一个指定的数；
（2）寻找某一个数的左侧边界或右侧边界；
（3）寻找某一个最佳值或位置，通过二分不断尝试找到。

如何判断是否需要使用二分
1）序列是有序的、且数据量巨大，需要对处理的时间复杂度进行优化；
2）给出一个要求达到的目标值，求出某个自变量能满足目标的最小/最大值，该自变量和目标之间存在单调关系（单调增或单调减）。注：大部分使用二分的场景存在单调关系，但不一定是必须的。

一、寻找一个指定的数

因为我们初始化 right = nums.length - 1，所以决定了我们的「搜索区间」是 [left, right]，所以决定了 while (left <= right)，同时也决定了 left = mid+1 和 right = mid-1。因为我们只需找到一个 target 的索引即可，所以当 nums[mid] == target 时可以立即返回。

点击查看代码

int binarySearch(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid;
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

1、为什么 while 循环的条件中是 <=，而不是 <？
答：因为初始化 right 的赋值是 nums.length - 1，即最后一个元素的索引，而不是 nums.length。
这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间 [left, right]，后者相当于左闭右开区间 [left, right)，因为索引大小为 nums.length 是越界的。
我们这个算法中使用的是前者 [left, right] 两端都闭的区间，这个区间其实就是每次进行搜索的区间。
2、为什么 left = mid + 1，right = mid - 1？我看有的代码是 right = mid 或者 left = mid，没有这些加加减减，到底怎么回事，怎么判断？
答：这也是二分查找的一个难点，不过只要你能理解前面的内容，就能够很容易判断。
刚才明确了「搜索区间」这个概念，而且本算法的搜索区间是两端都闭的，即 [left, right]。那么当我们发现索引 mid 不是要找的 target 时，下一步应该去搜索哪里呢？
当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对？因为 mid 已经搜索过，应该从搜索区间中去除。
3、此算法有什么缺陷？
答：至此，你应该已经掌握了该算法的所有细节，以及这样处理的原因。但是，这个算法存在局限性。
比如说给你有序数组 nums = [1,2,2,2,3]，target 为 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。这样的需求很常见，你也许会说，找到一个 target，然后向左或向右线性搜索不行吗？可以，但是不好，因为这样难以保证二分查找对数级的复杂度了。

二、寻找某一个数的左侧边界或右侧边界

1.寻找左侧边界的二分搜索

应用场景：

1. 找到第一个(大于)等于value的位置;（求下界）
2. 找到最后一个小于value的位置.（求上界，先求第一个大于大于value的位置，再将结果减1）

因为我们初始化 right = nums.length，所以决定了我们的「搜索区间」是 [left, right)，所以决定了 while (left < right)，同时也决定了 left = mid + 1 和 right = mid。因为我们需找到 target 的最左侧索引，所以当 nums[mid] == target 时不要立即返回，而要收紧右侧边界以锁定左侧边界

点击查看代码

int left_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0;
    int right = nums.length; // 注意

    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }

// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;
}

（1）为什么 while 中是 < 而不是 <=?
答：用相同的方法分析，因为 right = nums.length 而不是 nums.length - 1。因此每次循环的「搜索区间」是 [left, right) 左闭右开。while(left < right) 终止的条件是 left == right，此时搜索区间 [left, left) 为空，所以可以正确终止。
PS：这里先要说一个搜索左右边界和上面这个算法的一个区别，：刚才的 right 不是 nums.length - 1 吗，为啥这里非要写成 nums.length 使得「搜索区间」变成左闭右开呢？
因为对于搜索左右侧边界的二分查找，这种写法比较普遍，我就拿这种写法举例了，保证你以后遇到这类代码可以理解。你非要用两端都闭的写法反而更简单，我会在后面写相关的代码，把三种二分搜索都用一种两端都闭的写法统一起来。
（2）为什么没有返回 -1 的操作？如果 nums 中不存在 target 这个值，怎么办？
答：因为要一步一步来，先理解一下这个「左侧边界」有什么特殊含义：

对于这个数组，算法会返回索引 1。
这个索引 1 的含义可以解读为「nums 中小于 2 的元素有 1 个」。
比如对于有序数组 nums = [2,3,5,7], target = 1，算法会返回 0，含义是：nums 中小于 1 的元素有 0 个。再比如说 nums = [2,3,5,7], target = 8，算法会返回 4，含义是：nums 中小于 8 的元素有 4 个。
综上可以看出，函数的返回值（即 left 变量的值）取值区间是闭区间 [0, nums.length]，所以我们简单添加两行代码就能在正确的时候 return -1：

点击查看代码

while (left < right) {
    //...
}
// target 比所有数都大
if (left == nums.length) return -1;
// 类似之前算法的处理方式
return nums[left] == target ? left : -1;

（3）为什么 left = mid + 1，right = mid ？和之前的算法不一样？
答：这个很好解释，因为我们的「搜索区间」是 [left, right) 左闭右开，所以当 nums[mid] 被检测之后，下一步的搜索区间应该去掉 mid 分割成两个区间，即 [left, mid) 或 [mid + 1, right)。
（4）为什么该算法能够搜索左侧边界？
答：关键在于对于 nums[mid] == target 这种情况的处理：
if (nums[mid] == target)
right = mid;
可见，找到 target 时不要立即返回，而是缩小「搜索区间」的上界 right，在区间 [left, mid) 中继续搜索，即不断向左收缩，达到锁定左侧边界的目的。
（5）为什么返回 left 而不是 right？
答：都是一样的，因为 while 终止的条件是 left == right。
（6）能不能想办法把 right 变成 nums.length - 1，也就是继续使用两边都闭的「搜索区间」？这样就可以和第一种二分搜索在某种程度上统一起来了。
答：当然可以，只要你明白了「搜索区间」这个概念，就能有效避免漏掉元素，随便你怎么改都行。下面我们严格根据逻辑来修改：
因为你非要让搜索区间两端都闭，所以 right 应该初始化为 nums.length - 1，while 的终止条件应该是 left == right + 1，也就是其中应该用 <=：

点击查看代码

int left_bound(int[] nums, int target) {
    // 搜索区间为 [left, right]
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        // if else ...
    }

因为搜索区间是两端都闭的，且现在是搜索左侧边界，所以 left 和 right 的更新逻辑如下：

点击查看代码

if (nums[mid] < target) {
    // 搜索区间变为 [mid+1, right]
    left = mid + 1;
} else if (nums[mid] > target) {
    // 搜索区间变为 [left, mid-1]
    right = mid - 1;
} else if (nums[mid] == target) {
    // 收缩右侧边界
    right = mid - 1;
}

由于 while 的退出条件是 left == right + 1，所以当 target 比 nums 中所有元素都大时，会存在以下情况使得索引越界：

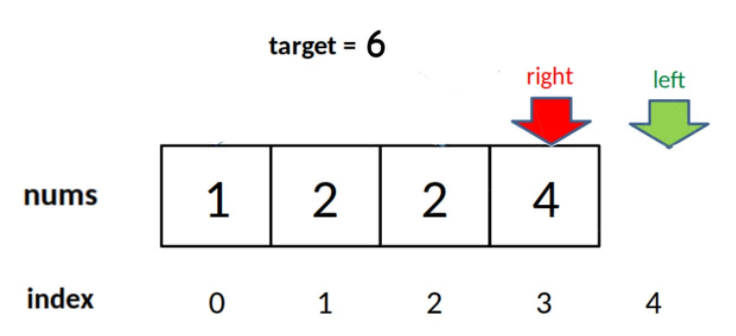
因此，最后返回结果的代码应该检查越界情况：

点击查看代码

if (left >= nums.length || nums[left] != target)
    return -1;
return left;

至此，整个算法就写完了，完整代码如下：

点击查看代码

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 检查出界情况
    if (left >= nums.length || nums[left] != target) {
        return -1;
    }
    return left;
}

这样就和第一种二分搜索算法统一了，都是两端都闭的「搜索区间」，而且最后返回的也是 left 变量的值。

2.寻找右侧边界的二分搜索

应用场景：
找到最后一个小于(等于)value的位置;（求上界）
找到第一个大于value的位置;（求下界）

因为我们初始化 right = nums.length，所以决定了我们的「搜索区间」是 [left, right)，所以决定了 while (left < right)，同时也决定了 left = mid + 1 和 right = mid。
因为我们需找到 target 的最右侧索引，所以当 nums[mid] == target 时不要立即返回，而要收紧左侧边界以锁定右侧边界。
又因为收紧左侧边界时必须 left = mid + 1，所以最后无论返回 left 还是 right，必须减一。

点击查看代码

int right_bound(int[] nums, int target) {
    if (nums.length == 0) return -1;
    int left = 0, right = nums.length;

    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            left = mid + 1; // 注意
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid;
        }
    }
    return left - 1; // 注意
}

3.统一模板

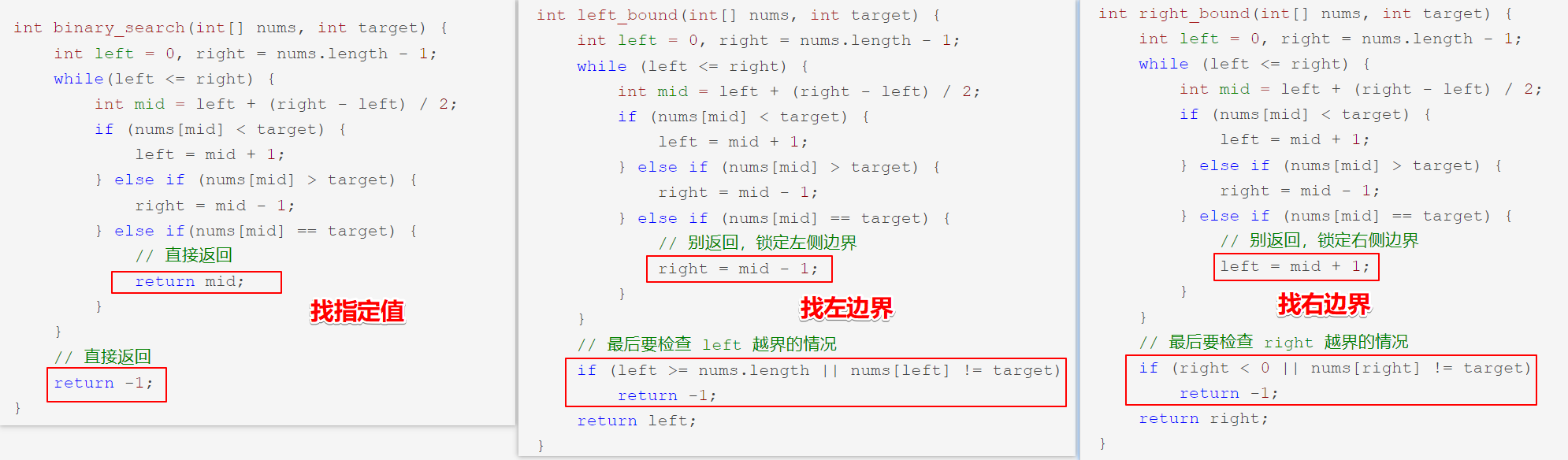
对于寻找左右边界的二分搜索，常见的方式是使用左闭右开的“搜索区间”，上面统一模板将“搜索区间”全部统一成了两端都闭，便于记忆，只需修改两处即可变化出3种写法。

点击查看代码

int binary_search(int[] nums, int target) {
    int left = 0, right = nums.length - 1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}

int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

三、寻找某一个最佳值或位置，通过二分不断尝试找到

首先，你要从题目中抽象出一个自变量x，一个关于x的函数f(x)，以及一个目标值target。
同时，x, f(x), target还要满足以下条件：
1、f(x)必须是在x上的单调函数（单调增单调减都可以）。
2、题目是让你计算满足约束条件f(x) == target时的x的值。

四、总结

1.二分法解法分类：

1） 采用系统自带函数进行解题
支持二分的数据结构：Arrays.binarySearch()、Collections.binarySearch()

内置方法binarySearch可以实现部分场景的二分查找：
严格递增序列场景：
a） lower_bound：返回目标值的下标，找不到则返回“0 - (插入点索引值 + 1)”
b） upper_bound：无
非严格递增序列场景：
a） lower_bound：如果目标值有重复，会随机返回其中一个的下标；找不到则返回“0 - (插入点索引值 + 1)”。
注：当目标值重复时，会获得随机下标，也可以通过向下遍历或向上遍历来获取lower_bound或upper_bound，这种方法也能解决大部分的场景。
b） upper_bound：无

点击查看代码

int[] arr = new int[] {1, 3, 5, 8, 8, 8, 9, 10, 11}; // 非递减序列

// 目标值7不是数组内元素，且值在数组范围内，从0开始计数，返回值 = 0 – (插入点索引值 + 1)
int index = Arrays.binarySearch(arr, 7);
System.out.println("find 7 = " + (index >= 0) + ", index = " + index); // find 7 = false, index = -4

// 8 搜索值是数组元素，从0开始计数，得搜索值的索引值（如果搜索值有多个会随机获取其中一个下标）
int lowerBound = Arrays.binarySearch(arr, 8);
System.out.println("lower_bound 8: index = " + lowerBound + ", value = " + arr[lowerBound]); // lower_bound 8: index = 4, value = 8

List<Integer> list = Arrays.asList(1,2,2,2,3);
System.out.println(Collections.binarySearch(list, 7)); // -6,不是数组内元素,返回值 = 0 – (插入点索引值 + 1)

从上面的例子可以看到，java内置方法binarySearch有较多的限制，若要实现类似C++的lower_bound/upper_bound，需要自己实现.
2） 自己写二分函数不断尝试获得目标值

点击查看代码

class Solution {
// 实现lower_bound、upper_bound功能
// bound=0表示lower_bound，bound=1表示upper_bound
    private static int binarySearch(int[] arr, int value, int bound) {
        int low = 0;
        int high = arr.length;
        while (low < high) {
            int mid = low + (high - low) / 2;
            boolean condition = (bound == 0) ? arr[mid] < value : arr[mid] <= value;
            if (condition) {
                low = mid + 1;
            } else {
                high = mid;
            }
        }
        return low;
    }

    public static void main(String[] args) {
        int[] array = new int[] {1, 3, 5, 8, 8, 8, 9, 10, 11};
        // 返回数组中第一个大于或等于被查数的值的下标
        int index = binarySearch(array, 7, 0);
        System.out.println("find 7 = " + (array[index] == 7));
        // lowerBound 返回数组中第一个大于或等于被查数的值的下标
        int lowerBound = binarySearch(array, 8, 0);
        System.out.println("lower_bound 8: index = " + lowerBound + ", value = " + array[lowerBound]);
        // upperBound 返回数组中第一个大于被查数的值的下标
        int upperBound = binarySearch(array, 8, 1);
        System.out.println("upper_bound 8: index = " + upperBound + ", value = " + array[upperBound]);
    }
}

输出结果： find 7 = false lower_bound 8: index = 3, value = 8 upper_bound 8: index = 6, value = 9

2.练习题

场景一（使用系统库函数）
找值
1）704. 二分查找：https://leetcode-cn.com/problems/binary-search/
lowbound
1）35. 搜索插入位置：https://leetcode-cn.com/problems/search-insert-position/
2）1712. 将数组分成三个子数组的方案数：https://leetcode-cn.com/problems/ways-to-split-array-into-three-subarrays/
upperbound
1712. 将数组分成三个子数组的方案数：https://leetcode-cn.com/problems/ways-to-split-array-into-three-subarrays/

场景二（自己写二分函数）
找值
1）633. 平方数之和：https://leetcode-cn.com/problems/sum-of-square-numbers/
2）69. x 的平方根：https://leetcode-cn.com/problems/sqrtx/
3）剑指 Offer 53 - II. 0～n-1中缺失的数字：https://leetcode-cn.com/problems/que-shi-de-shu-zi-lcof/
lowbound
1）875 爱吃香蕉的珂珂：https://leetcode-cn.com/problems/koko-eating-bananas/
2）658. 找到 K 个最接近的元素：https://leetcode-cn.com/problems/find-k-closest-elements/
3）275. H 指数 II：https://leetcode-cn.com/problems/h-index-ii/
4）1300. 转变数组后最接近目标值的数组和：https://leetcode-cn.com/problems/sum-of-mutated-array-closest-to-target/
5）410. 分割数组的最大值：https://leetcode-cn.com/problems/split-array-largest-sum/
upperbound
1）1552. 两球之间的磁力：https://leetcode-cn.com/problems/xiao-zhang-shua-ti-ji-hua/solution/

参考链接：
【1】我写了首诗，让你闭着眼睛也能写对二分搜索 :: labuladong的算法小抄
【2】我写了一个套路，助你随心所欲运用二分搜索