Leetcode---1.二叉树篇
♥♥♥二叉树题目的递归解法可以分两类思路：
- 第一类是遍历一遍二叉树得出答案（回溯算法核心框架）
- 第二类是通过分解问题计算出答案（动态规划核心框架）
遇到一道二叉树的题目时的通用思考过程是：
是否可以通过遍历一遍二叉树得到答案？如果不能的话，是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？
一、二叉树
1.前中后序遍历
二叉树遍历框架：
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
traverse(root.left);
// 中序位置
traverse(root.right);
// 后序位置
}
前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝不仅仅是三个顺序不同的 List：
- 前序位置的代码在刚刚进入一个二叉树节点的时候执行；
- 后序位置的代码在将要离开一个二叉树节点的时候执行；
- 中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。
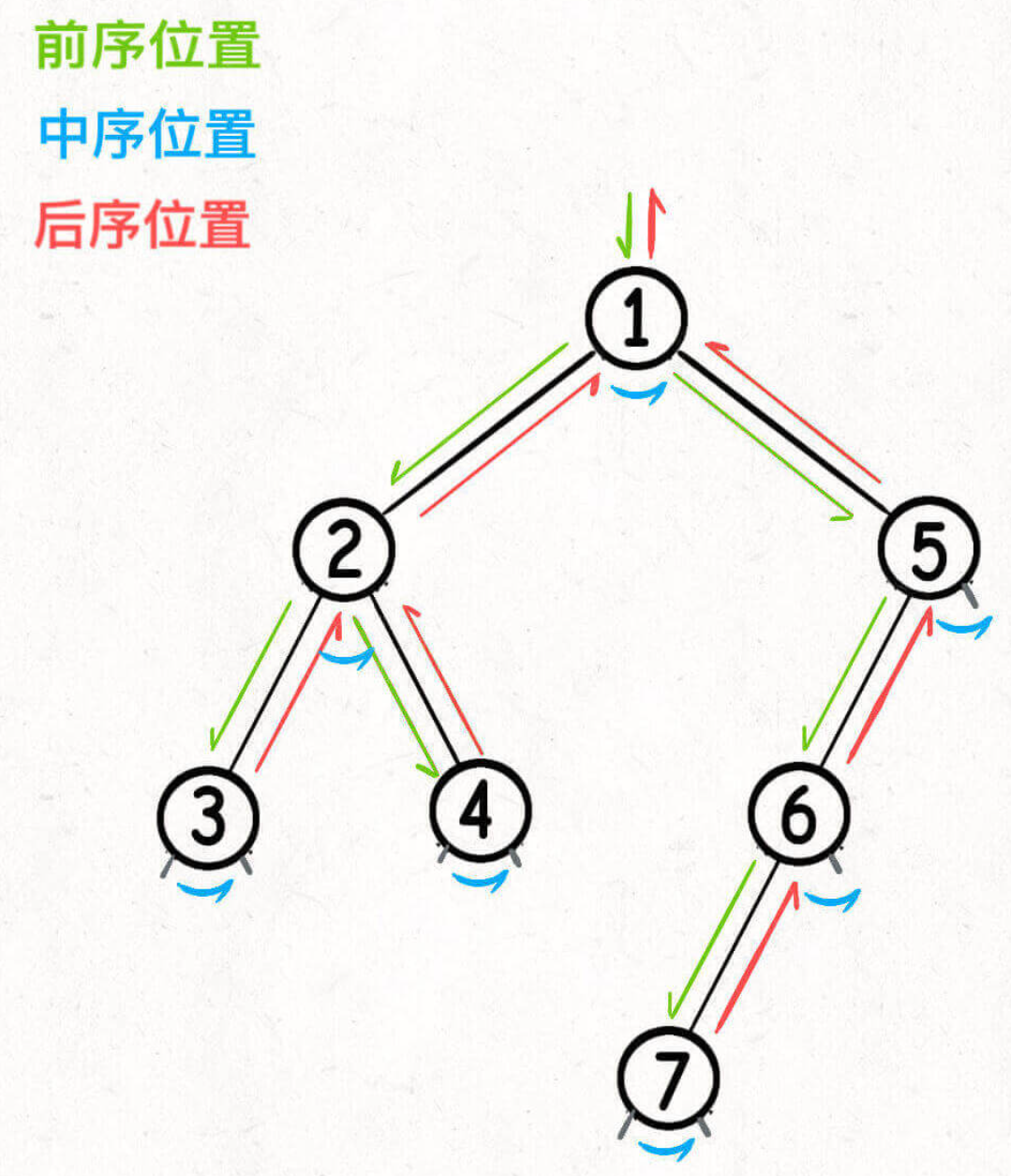
后序位置的特殊之处
- 中序位置主要用在 BST 场景中，你完全可以把 BST 的中序遍历认为是遍历有序数组。
- 前序位置本身其实没有什么特别的性质，之所以你发现好像很多题都是在前序位置写代码，实际上是因为我们习惯把那些对前中后序位置不敏感的代码写在前序位置罢了。
- 后序位置和前序位置对比，发现前序位置的代码执行是自顶向下的，而后序位置的代码执行是自底向上的。这意味着前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。
2.层序遍历
// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {
if (root == null) return;
Queue<TreeNode> q = new LinkedList<>();
q.offer(root);
// 从上到下遍历二叉树的每一层
while (!q.isEmpty()) {
int sz = q.size();
// 从左到右遍历每一层的每个节点
for (int i = 0; i < sz; i++) {
TreeNode cur = q.poll();
// 将下一层节点放入队列
if (cur.left != null) {
q.offer(cur.left);
}
if (cur.right != null) {
q.offer(cur.right);
}
}
}
}
这里面 while 循环和 for 循环分管从上到下和从左到右的遍历：
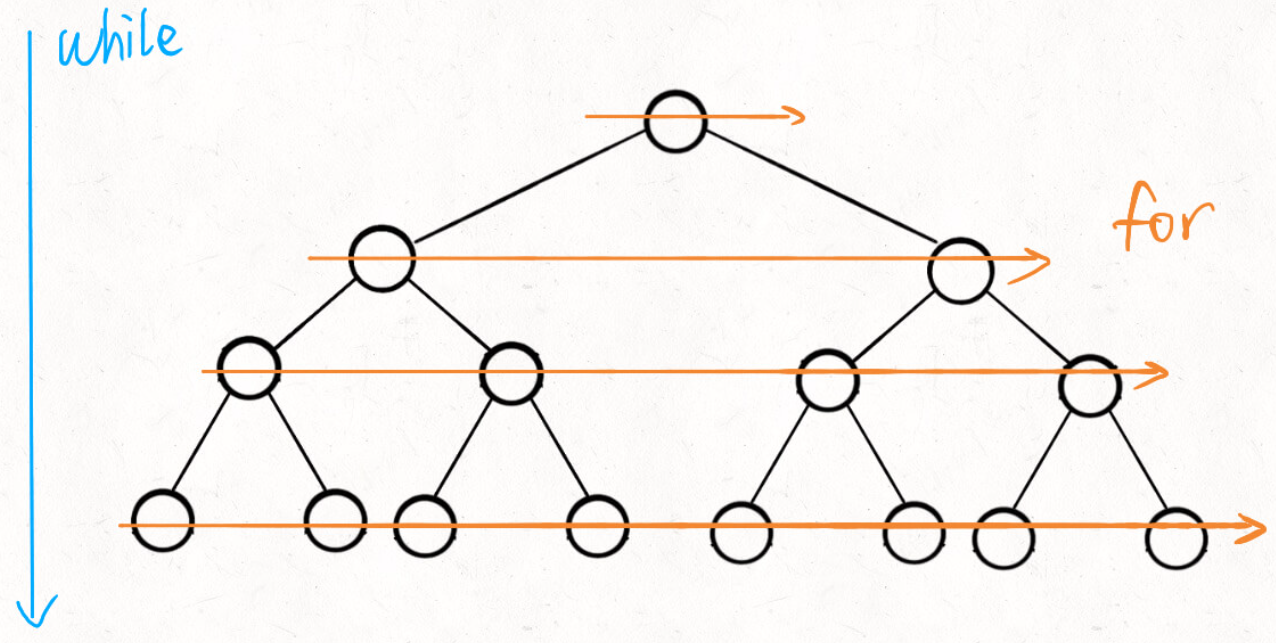
BFS 算法框架 就是从二叉树的层序遍历扩展出来的，常用于求无权图的最短路径问题。
二、多叉树
多叉树遍历框架
/* 基本的 N 叉树节点 */
class TreeNode {
int val;
TreeNode[] children;
}
void traverse(TreeNode root) {
for (TreeNode child : root.children)
traverse(child);
}
N 叉树的遍历又可以扩展为图的遍历，因为图就是好几 N 叉棵树的结合体。你说图是可能出现环的？这个很好办，用个布尔数组 visited 做标记就行了。
参考链接：
【1】手把手带你刷二叉树（第一期） :: labuladong的算法小抄
