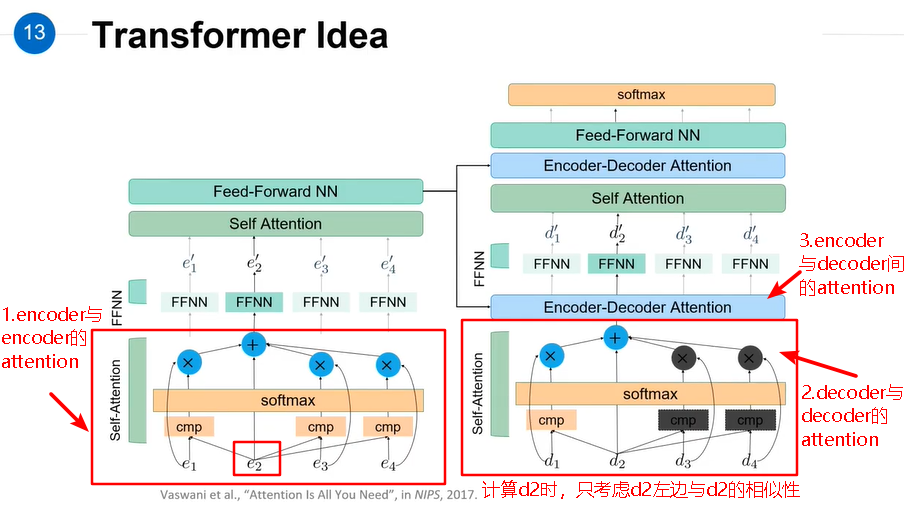
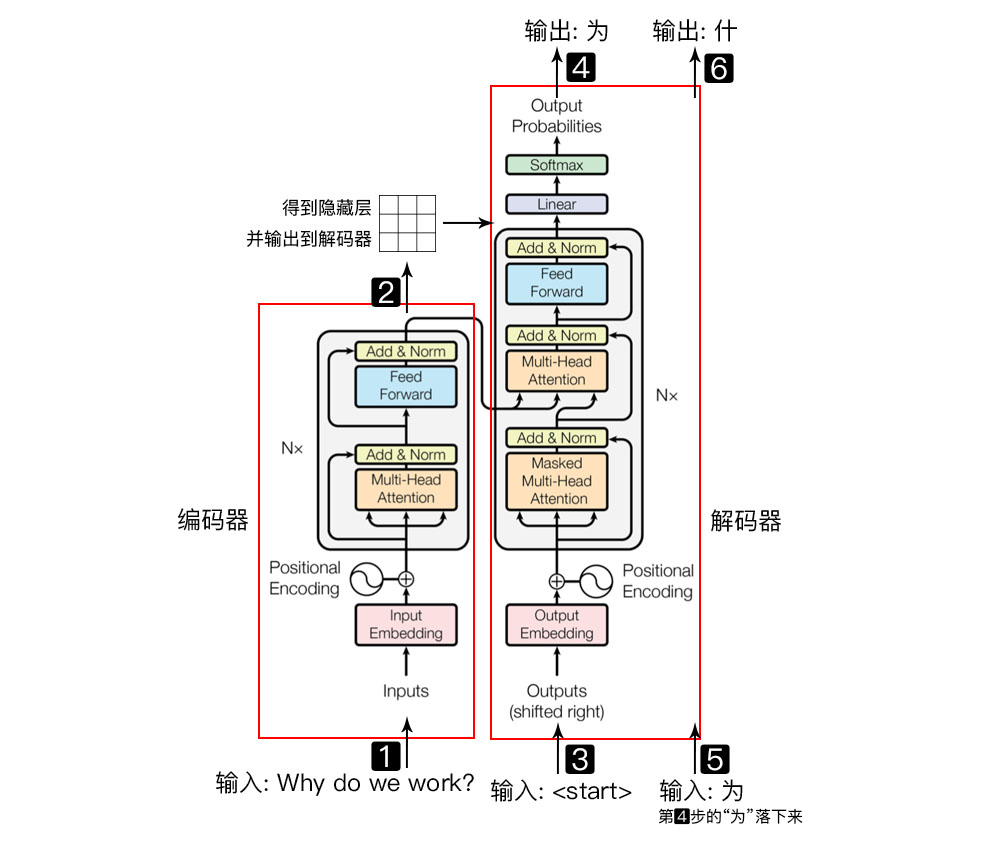
Transformer模型---encoder

一、简介

论文：《Attention is all you need》

作者：Google团队（2017年发表在NIPS上）

简介：Transformer 是一种新的、基于 attention 机制来实现的特征提取器，可用于代替 CNN 和 RNN 来提取序列的特征。 在该论文中 Transformer 用于 encoder - decoder 架构。事实上 Transformer 可以单独应用于 encoder 或者单独应用于 decoder 。
  1. 输入自然语言序列到编码器: Why do we work?(为什么要工作);
  2. 编码器输出的隐藏层, 再输入到解码器;
  3. 输入$<start>$(起始)符号到解码器;
  4. 得到第一个字"为";
  5. 将得到的第一个字"为"落下来再输入到解码器;
  6. 得到第二个字"什";
  7. 将得到的第二字再落下来, 直到解码器输出$<end>$(终止符), 即序列生成完成。
 

Transformer相比较LSTM等循环神经网络模型的优点：

  • 可以直接捕获序列中的长距离依赖关系；
  • 模型并行度高，使得训练时间大幅度降低。

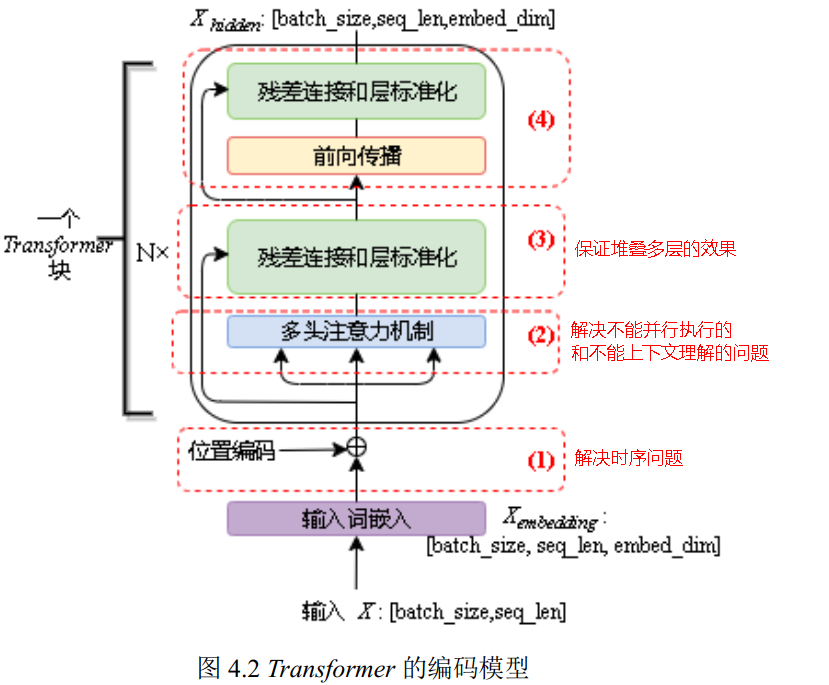
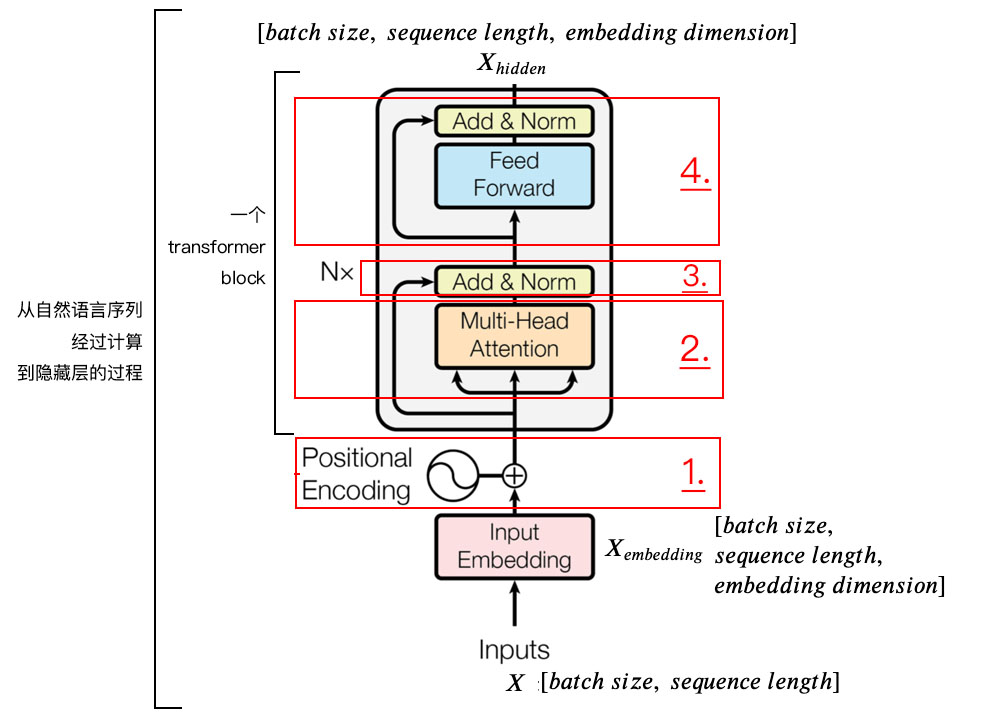
二、编码器

1) 字向量与位置编码

$X = EmbeddingLookup(X) + PositionalEncoding$
$X \in \mathbb{R}^{batch \ size \ * \ seq. \ len. \ * \ embed. \ dim.} $
2) 自注意力机制
$Q = Linear(X) = XW_{Q}$
$K = Linear(X) = XW_{K}$
$V = Linear(X) = XW_{V}$
$X_{attention} = SelfAttention(Q, \ K, \ V)$
3) 残差连接与Layer Normalization
$X_{attention} = X + X_{attention}$
$X_{attention} = LayerNorm(X_{attention})$
4) $FeedForward$, 其实就是两层线性映射并用激活函数激活, 比如说$ReLU$：
$X_{hidden} = Activate(Linear(Linear(X_{attention})))$
5) 重复3)：
$X_{hidden} = X_{attention} + X_{hidden}$
$X_{hidden} = LayerNorm(X_{hidden})$
$X_{hidden} \in \mathbb{R}^{batch \ size \ * \ seq. \ len. \ * \ embed. \ dim.} $

1.positional encoding

　　由于transformer模型没有循环神经网络的迭代操作，所以我们必须提供每个字的位置信息给transformer，才能识别出语言中的顺序关系。

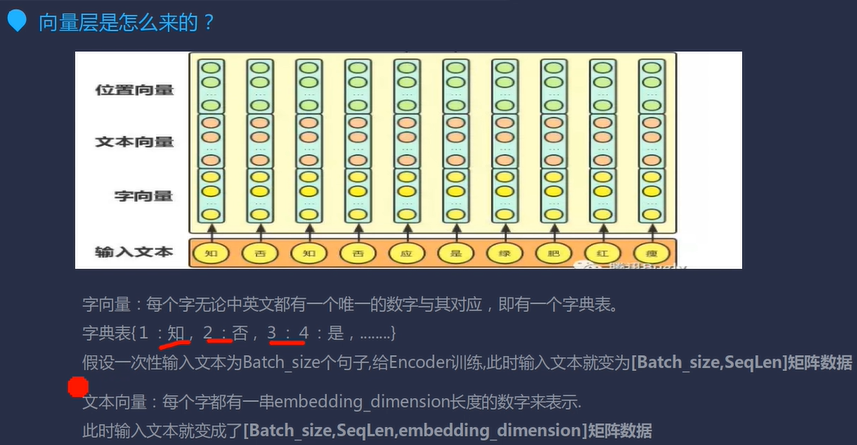
（1）字向量

每个字无论中英文都有一个唯一的数字与其对应，即有一个字典表。

字典表：{1：知，2：否，3：应，...}

 

  

（2）文本向量

假设一次性输入文本为batch_size个句子，给encoder训练，此时输入文本就变为[batch_size,seq_len]矩阵数据。

文本向量：每个字都有一串embed_dim长度的数字来表示。

  

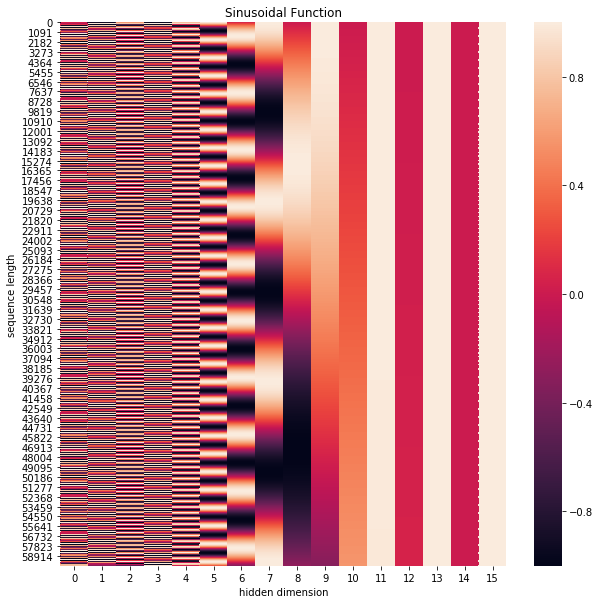
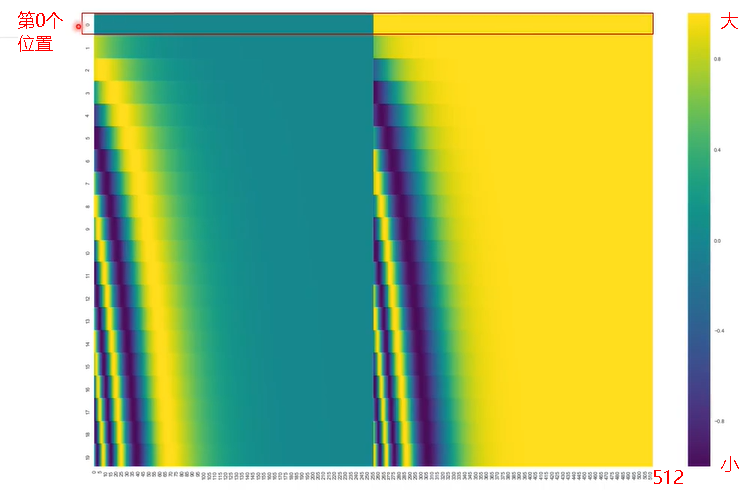
（3）位置向量positional encoding

  1. 买张北京到广州的机票。

  2. 买张广州到北京的机票。

　　位置向量的维度为[max_seq_len，embed_dim]，max_seq_len属于超参数, 指的是限定的最大单个句长。 
注意, 我们一般以字为单位训练transformer模型, 也就是说我们不用分词了, 首先我们要初始化字向量为[vocab_size, embed_dim]，vocab_size为总共的字库数量，embed_dim为字向量的维度，也是每个字的数学表达。

下面画一下位置嵌入, 可见纵向观察, 随着embed_dim增大, 位置嵌入函数呈现不同的周期变化。

注意力矩阵的三维图如下：

论文中使用了$sine$和$cosine$函数的线性变换来提供给模型位置信息:

$PE_{(pos,2i)} = sin(\frac{pos} {10000^{2i/d_{model}}})$

$PE_{(pos,2i+1)} = cos(\frac{pos}{10000^{2i/d_{model}}})$

  1. 上式中$pos$指的是句中字的位置, 取值范围是[0, max_seq_len)，

  2. $i$指的是词向量的维度, 取值范围是[0, embed_dim)，

  3. $d_{model}$指的是字向量的最大维度即embed_dim最大值，$d_{model}=512$。                                            

       上面有$sin$和$cos$一组公式, 也就是对应着embed_dim维度的一组奇数和偶数的序号的维度, 例如$0,1$一组，$2,3$一组, 分别用上面的$sin$和$cos$函数做处理，从而产生不同的周期性变化，而位置嵌入在embed_dim维度上随着维度序号增大，周期变化会越来越慢，而产生一种包含位置信息的纹理，就像Transformer论文原文第六页讲的，位置嵌入函数的周期从$2 \pi$到$10000 * 2 \pi$变化，而每一个位置在embed_dim维度上都会得到不同周期的$sin$和$cos$函数的取值组合，从而产生独一的纹理位置信息，模型从而学到位置之间的依赖关系和自然语言的时序特性。

相对位置编码与绝对位置编码：

  1. 你好，买张北京到广州的机票。（绝对，BERT）

  2. 买张北京到广州的机票。（相对） 

  

2. self-attention mechanism

（1）为什么用self-attention？

（2）什么是self-attention？

1.Encoder

2.Decoder 

3.Encoder-Decoder  

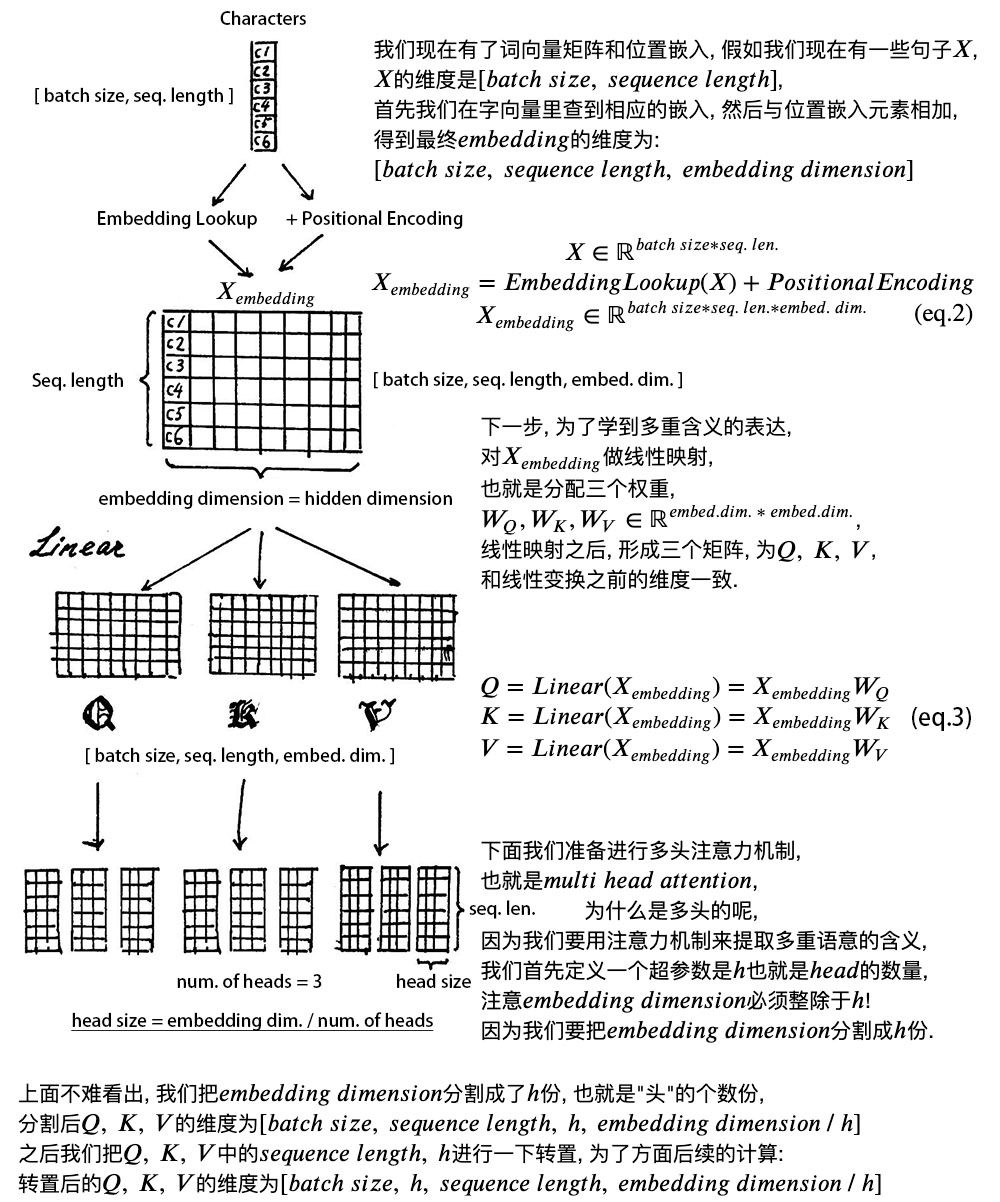
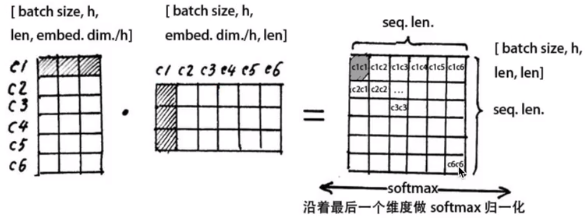
（3）怎么计算self-attention？

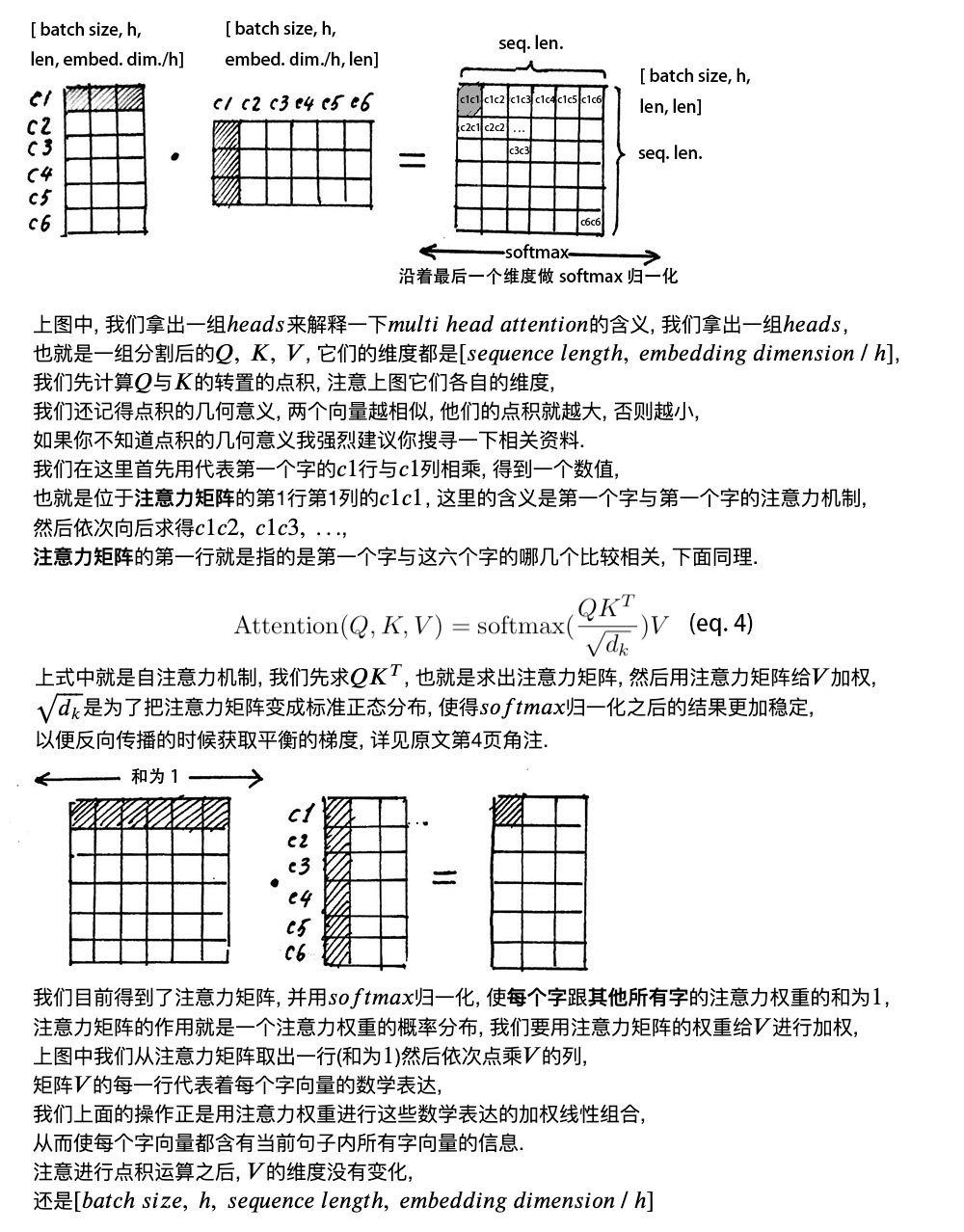
Attention Mask

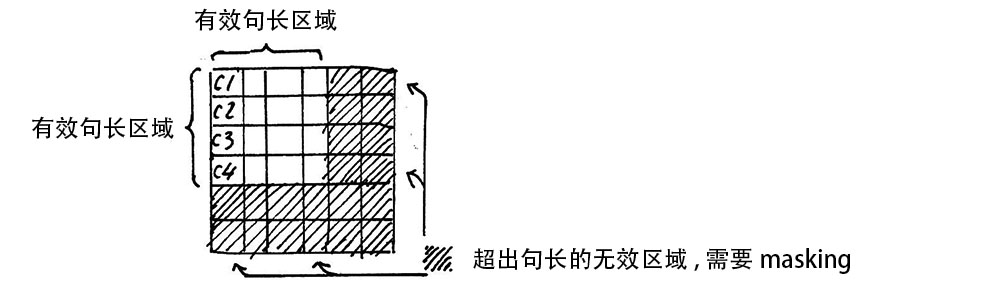
　　注意, 在上面self attention的计算过程中, 我们通常使用mini batch来计算, 也就是一次计算多句话, 也就是X的维度是[batch_size, seq_len], seq_len是句长, 而一个mini batch是由多个不等长的句子组成的, 我们就需要按照这个mini batch中最大的句长对剩余的句子进行补齐长度, 我们一般用0来进行填充, 这个过程叫做padding。
　　但这时在进行softmax的时候就会产生问题, 回顾softmax函数$\sigma (\mathbf {z} )_{i}={\frac {e^{z_{i}}}{\sum _{j=1}^{K}e^{z_{j}}}}$, $e^0$是1, 是有值的, 这样的话softmax中被padding的部分就参与了运算, 就等于是让无效的部分参与了运算, 会产生很大隐患, 这时就需要做一个mask让这些无效区域不参与运算, 我们一般给无效区域加一个很大的负数的偏置, 也就是:
$z_{illegal} = z_{illegal} + bias_{illegal}$
$bias_{illegal} \to -\infty$
$e^{z_{illegal}} \to 0 $
经过上式的masking我们使无效区域经过softmax计算之后还几乎为0, 这样就避免了无效区域参与计算。

（4）多头自注意力机制

综合CNN和self-attention，考虑不同类型的关系。

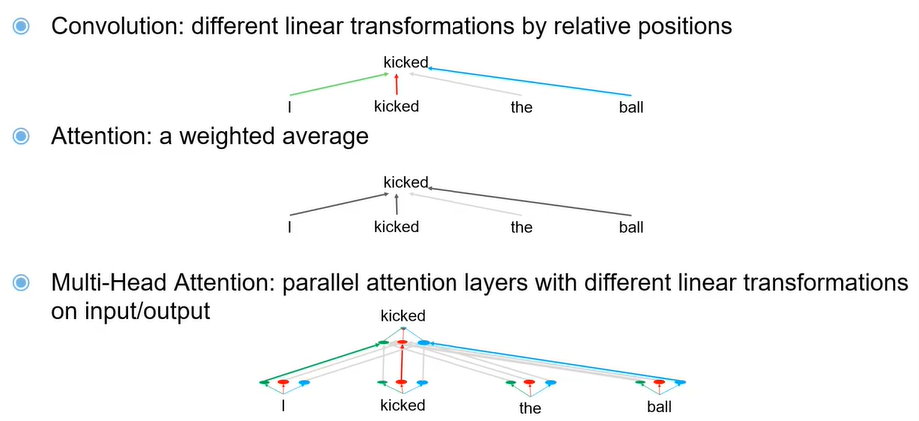
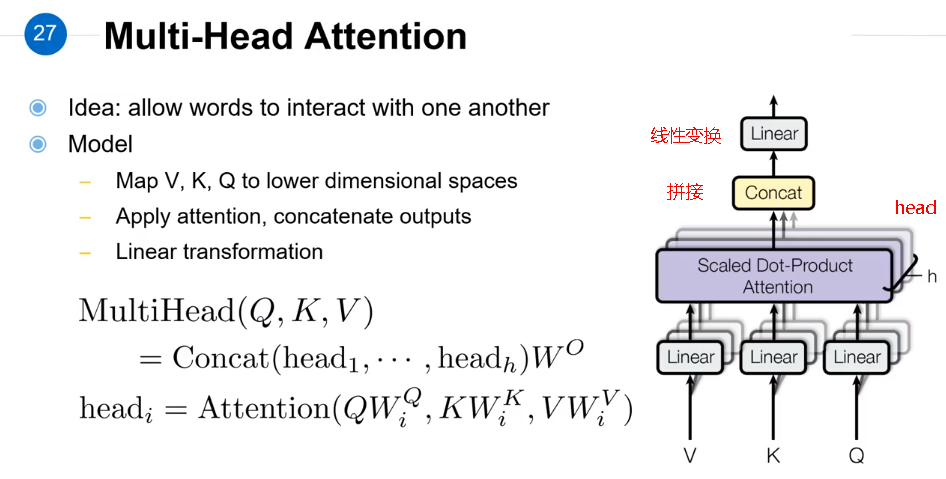
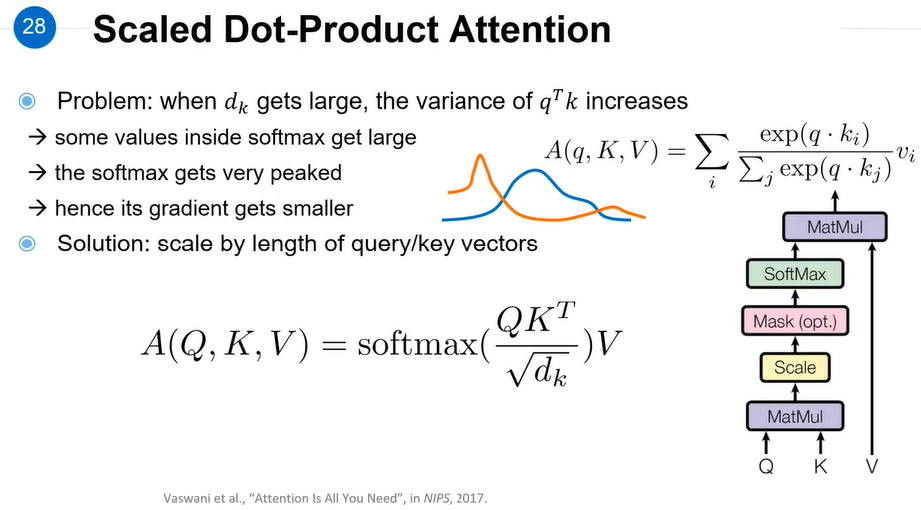
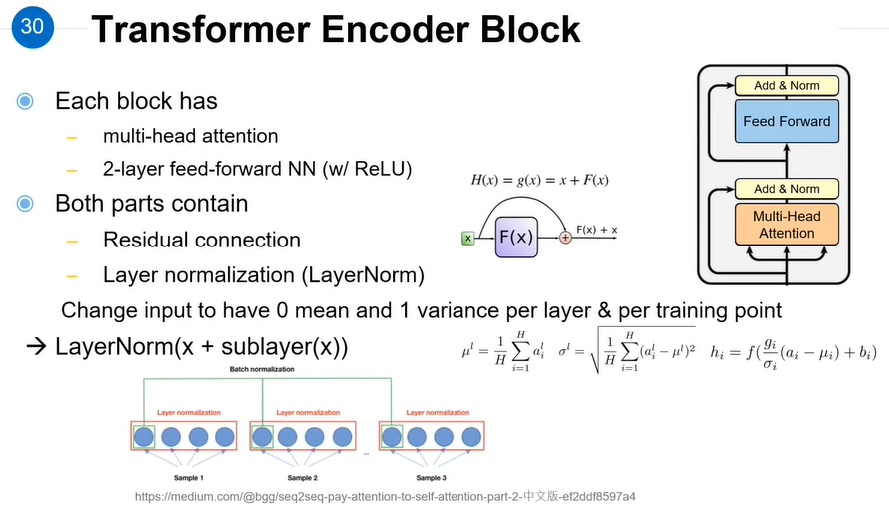
3. 残差连接和层标准化

（1）残差连接residual connection

我们在上一步得到了经过注意力矩阵加权之后的$V$, 也就是$Attention(Q, K, V)$, 我们对它进行一下转置, 使其和$X_{embedding}$的维度一致, 也就是[batch_size, seq_len, embed_dim], 然后把他们加起来做残差连接, 直接进行元素相加, 因为他们的维度一致: 
$X_{embedding} + Attention(Q, \ K, \ V)$
在之后的运算里, 每经过一个模块的运算, 都要把运算之前的值和运算之后的值相加, 从而得到残差连接, 训练的时候可以使梯度直接走捷径反传到最初始层:
$X + SubLayer(X)$

 

 

  

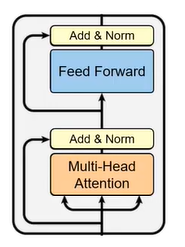
（2）层标准化layer normalization

$Layer Normalization$的作用是把神经网络中隐藏层归一为标准正态分布, 也就是$i.i.d$独立同分布, 以起到加快训练速度, 加速收敛的作用:
$\mu_{i}=\frac{1}{m} \sum^{m}_{i=1}x_{ij}$
上式中以矩阵的行$(row)$为单位求均值;
$\sigma^{2}_{j}=\frac{1}{m} \sum^{m}_{i=1}(x_{ij}-\mu_{j})^{2}$
上式中以矩阵的行$(row)$为单位求方差;
$LayerNorm(x)=\alpha \odot \frac{x_{ij}-\mu_{i}}{\sqrt{\sigma^{2}_{i}+\epsilon}} + \beta$
然后用每一行的每一个元素减去这行的均值, 再除以这行的标准差, 从而得到归一化后的数值, $\epsilon$是为了防止除0; 
之后引入两个可训练参数$\alpha, \beta$来弥补归一化的过程中损失掉的信息, 注意$\odot$表示元素相乘而不是点积, 我们一般初始化$\alpha$为全1, 而$\beta$为全0

4. 训练tips

5.总结

 

 

 

参考文献：

【1】大师级的a_journey_into_math_of_ml / 04_transformer_tutorial_2nd_part·浓缩咖啡/浓咖啡/ a_journey_into_math_of_ml

【2】The Illustrated Transformer（可视化讲解）

【3】The Annotated Transformer（代码讲解）

【4】TensorFlow实战BERT

【5】台大《应用深度学习》国语课程(2020) by 陈蕴侬

【6】带注释的变压器

posted @ 2019-11-27 20:11  nxf_rabbit75  阅读(3685)  评论(0)  编辑  收藏  举报