29.聚类---性能度量
一、性能度量
聚类的性能度量也称作聚类的有效性指标。
聚类的性能度量分两类：
- 聚类结果与某个参考模型进行比较，称作外部指标；
- 直接考察聚类结果而不利用任何参考模型，称作内部指标。
1. 外部指标
对于数据集$D={x_1,x_2,...,x_N}$，假定通过聚类给出的簇划分为$C={C_1,C_2,...,C_K}$，参考模型给出的簇划分为$C^*=\{C_1^*,C_2^*,...,C_K^*\}$，其中$K$和$K'$不一定相等。
令$\lambda,\lambda^*$分别表示$C,C^*$的簇标记向量。定义：
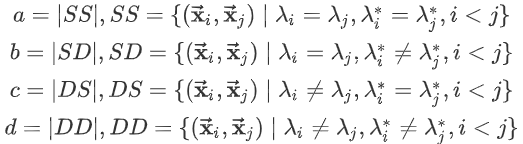
其中|·|表示集合的元素的个数，各集合的意义为：
- $SS$：包含了同时隶属于$C,C^*$的样本对；
- $SD$：包含了隶属于$C$，但是不隶属于$C^*$的样本对；
- $DS$：包含了不隶属于$C$，但是隶属于$C^*$的样本对；
- $DD$：包含了同时不隶属于$C,C^*$的样本对；
由于每个样本对$(x_i,x_j)$，$i<j$仅能出现在一个集合中，因此有
$a+b+c+d=\frac{N(N-1)}{2}$
下面性能度量的结果都在[0,1]之间，这些值越大，说明聚类的性能越好。
1.1 Jaccard系数
Jaccard系数Jaccard Coefficient：$JC=\frac{a}{a+b+c}$
它刻画了所有的同类的样本对（要么在C中属于同类，要么在C*中属于同类）中，同时隶属于$C,C^*$的样本对的比例。
1.2 FM指数
FM指数Fowlkes and Mallows Index：$FMI=\sqrt{\frac{a}{a+b} · \frac{a}{a+c}}$
它刻画的是：
- 在$C$中同类的样本对中，同时隶属于$C^*$的样本对的比例为$p1=\frac{a}{a+b}$
- 在$C^*$中同类的样本对中，同时隶属于$C$的样本对的比例为$p2=\frac{a}{a+c}$
- FMI就是$p1$和$p2$的几何平均。
1.3 Rand指数
Rand指数Rand Index：$RI=\frac{a+d}{N(N-1)/2}$
它刻画的是：
- 同时隶属于$C,C^*$的同类样本对（这种样本对属于同一个簇的概率最大）与既不隶属于$C$、又不隶属于$C^*$的非同类样本对（这种样本对不是同一个簇的概率最大）之和，占所有样本对的比例。
- 这个比例其实就是聚类的可靠程度的度量。
1.4 ARI指数
使用RI有关问题：对于随机聚类，RI指数不保证接近0（可能还很大）。
ARI指数就通过利用随机聚类来解决这个问题。
定义一致性矩阵为：
其中：
- $s_i$为属于簇$C_i$的样本的数量，$t_i$为属于簇$C_i^*$的样本的数量。
- $n_{i,j}$为同时属于簇$C_i$和簇$C_i^*$的样本的数量。
则根据定义有：$\sum_i \sum_j C_{n_{i,j}}^2$，其中$C_n^2=\frac{n(n-1)}{2}$表示组合数，数字2是因为需要提取两个样本组成样本对。
定义ARI指数Adjusted Rand Index：
- 随机挑选一对样本，一共有$C_N^2$种情形。
- 这对样本隶属于$C$中的同一个簇，一共有$\sum_i C_{s_i}^2$种可能。
- 这对样本隶属于$C^*$中的同一个簇，一共有$\sum_j C_{t_j}^2$种可能。
- 这对样本隶属于$C$中的同一个簇、且属于$C^*$中的同一个簇，一共有$\sum_i C_{s_i}^2 \sum_j C_{t_j}^2$种可能。
- 则在随机划分的情况下，同时隶属于$C,C^*$的样本对的期望为：$[\sum_i C_{s_i}^2 \sum_j C_{t_j}^2]/C_N^2$
2. 内部指标
对于数据集$D={x_1,x_2,...,x_N}$，假定通过聚类给出的簇划分为$C={C_1,C_2,...,C_K}$
定义：
其中，$distance(x_i,x_j)$表示两点$x_i,x_j$之间的距离；$u_k$表示簇$C_k$的中心点，$u_l$表示簇$C_l$的中心点，$distance(u_k,u_l)$表示簇$C_k,C_l$的中心点之间的距离。
2.1 DB指数
DB指数Davies-Bouldin Index：$DBI=\frac{1}{K} \sum_{k=1}^K max_{k \ne l}(\frac{avg(C_k+avg(C_l))}{d_{cen}(C_k,C_l)})$
其物理意义为：
- 给定两个簇，每个簇样本距离均值之和比上两个簇的中心点之间的距离作为度量。该度量越小越好。
- 给定一个簇k，遍历其他的簇，寻找该度量的最大值。
- 对所有的簇，取其最大度量的均值。
DBI越小越好，
- 如果每个簇样本距离均值越小（即簇内样本距离都很近），则DBI越小。
- 如果簇间中心点的距离越大（即簇间样本距离相互都很远），则DBI越小。
2.2 Dunn指数
Dunn指数Dunn Index：$DI=\frac{min_{k \ne l} d_{min}(C_k,C_l)}{max_i diam(C_i)}$
其物理意义为：任意两个簇之间最近的距离的最小值，除以任意一个簇内距离最远的两个点的距离的最大值。
DI越大越好，
- 如果任意两个簇之间最近的距离的最小值越大（即簇间样本距离相互都很远），则DI越大。
- 如果任意一个簇内距离最远的两个点的距离的最大值越小（即簇内样本距离都很近），则DI越大。
3. 距离度量
3.1 闵可夫斯基距离Minkowski distance
给定样本$X_i=(x_{i,1},x_{i,2},...,x_{i,n})$，$X_j=(x_{j,1},x_{j,2},...,x_{j,n})$，则闵可夫斯基距离定义为：$distance(X_i,X_j)=(\sum_{d=1}^n |x_{i,d}-x_{j,d}|^p)^{1/p}$
- 当$p=2$时，闵可夫斯基距离就是欧式距离Euclidean distance：$distance(X_i,X_j)=||X_i-X_j||_2=\sqrt{\sum_{d=1}^n |x_{i,d}-x_{j,d}|^2)}$
- 当$p=1$时，闵可夫斯基距离就是曼哈顿距离Euclidean distance：$distance(X_i,X_j)=||X_i-X_j||_1=\sum_{d=1}^n |x_{i,d}-x_{j,d}|$
3.2 VDM距离 value Difference Metric
考虑非数值类属性（如属性取值为：中国，印度，美国，英国），令$m_{d,a}$表示$x_d=a$的样本数；$m_{d,a,k}$表示$x_d=a$且位于簇$C_k$中的样本的数量。则在属性$d$上的两个取值$a,b$之间的VDM距离为：
$VDM_p(a,b)=(\sum_{k=1}^K | \frac{m_{d,a,k}}{m_{d,a}} - \frac{m_{d,b,k}}{m_{d,b}}|^p)^{1/p}$
该距离刻画的是：属性取值在各簇上的频率分布之间的差异。
3.3 混合距离
当样本的属性为数值属性与非数值属性混合时，可以将闵可夫斯基距离与VDM距离混合使用。
假设属性$x_1,x_2,...,x_{n_c}$为数值属性，属性$x_{n_c+1},x_{n_c+2},...,x_n$为非数值属性。则：$distance(X_i,X_j)=(\sum_{d=1}^{n_c} |x_{i,d} - x_{j,d}|^p + \sum_{d=n_c+1}^{n} VDM_p(x_{i,d},x_{j,d})^p)^{1/p}$
3.4 加权距离
当样本空间中不同属性的重要性不同时，可以采用加权距离。以加权闵可夫斯基距离为例：$distance(X_i,X_j)=(\sum_{d=1}^{n}w_d |x_{i,d}-x_{j,d}|^p)^{1/p}，w_d >= 0,d=1,2,...,n;\sum_{d=1}^n w_d=1$
这里的距离度量满足三角不等式：$distance(X_i,X_j)<=distance(X_i,X_k)+distance(X_k,X_j)$
【注意】余弦距离不是一个严格定义的距离，其满足正定性，对称性，但是不满足三角不等式。余弦相似度在高维的情况下依然保持“相同时为1，正交时为0，相反时为-1”的性质。欧式距离的数值受维度的影响，范围不固定，并且含义也比较模糊。欧式距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异。
