8.2 数据结构---字符串（查找）

posted @   nxf_rabbit75  阅读(360)  评论(0)  编辑  收藏  举报
undefined
undefined

最长公共子序列 & 最长公共子串的区别：

找两个字符串的最长公共子串，这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。

一、最长连续公共子串

题目:  找出两个字符串的最长连续公共子串
例: abccade 和 dgcadde ==> cad

思路：动态规划 

考虑两种情况：

M[i+1][j+1]=0,             s1[i+1] != s2[j+1]

M[i+1][j+1]=M[i][j]+1,  s1[i+1] == s2[j+1]


时间复杂度O(M*N)
空间复杂度O(M*N)

 

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def getMaxSubStr(s1,s2):
    len_s1 = len(s1)
    len_s2 = len(s2)
    sb = ''
    maxs = 0 #记录最长公共子串的长度
    maxI = 0 #记录最长公共子串的最后一个字符的位置
    M = [([None] * (len_s2+1)) for i in range(len_s1+1)]
    i = 0
    while i < len_s1 + 1:
        M[i][0] = 0
        i += 1
    j = 0
    while j < len_s2 + 1:
        M[0][j] = 0
        j += 1
    #通过利用递归公式填写新建的二维数组
    i = 1
    while i < len_s1 + 1:
        j = 1
        while j < len_s2 + 1:
            if list(s1)[i-1] == list(s2)[j-1]:
                M[i][j] = M[i-1][j-1] + 1
                if M[i][j] > maxs:
                    maxs = M[i][j]
                    maxI = i
            else:
                M[i][j] = 0
            j += 1
        i += 1
    i = maxI - maxs
    while i < maxI:
        sb = sb + list(s1)[i]
        i += 1
    return sb
 
s1 = 'abcdefg'
s2 = 'bdeg'
res = getMaxSubStr(s1,s2)
print(res)

结果如下：

 

二、最长公共子序列(非必须连续)

题目: 找出两个字符串的最长公共子序列（非连续）

举例: abcbdab和bdcaba ==》 bcba

思路：动态规划，

　　　　M[i][j]=0,　　  　　　　　　　　i=0,j=0

　　　　M[i][j]=M[i-1][j-1] + 1         　　  i,j>0,xi=yi

　　　　M[i][j]=max{M[i-1][j],M[i][j-1]}   i,j>0,xi!=yi

 

　　      S[i][j]=1        s1[i] == s2[j]

　　　  S[i][j]=2        s1[i] != s2[j] 且 M[i-1][j] >=M[i][j-1]

　　　  S[i][j]=3        s1[i] != s2[j] 且 M[i-1][j] < M[i][j-1]

 

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
def LCS(s1,s2):
    #s1行，s2列
    len_s1 = len(s1)
    len_s2 = len(s2)
    sb = ''
    M = [([None] * (len_s2+1)) for i in range(len_s1+1)]
    S = [([None] * (len_s2+1)) for i in range(len_s1+1)]
    i = 0
    while i < len_s1 + 1:
        M[i][0] = 0
        S[i][0] = 0
        i += 1
    j = 0
    while j < len_s2 + 1:
        M[0][j] = 0
        S[0][j] = 0
        j += 1
    #通过利用递归公式填写新建的二维数组
    i = 1
    while i < len_s1 + 1:
        j = 1
        while j < len_s2 + 1:
            if s1[i-1] == s2[j-1]:
                M[i][j] = M[i-1][j-1] + 1
                S[i][j] = 1
            elif M[i-1][j] >= M[i][j-1]:
                M[i][j] = M[i-1][j]
                S[i][j] = 2
            else:
                M[i][j] = M[i][j-1]
                S[i][j] = 3
            j += 1
        i += 1
    # print(M)
    return M[-1][-1],S
 
def cLCS(i,j,S,s1):
    if i == 0 or j == 0:
        return
    if S[i][j] == 1:
        cLCS(i-1,j-1,S,s1)
        print (s1[i - 1], end='')
    elif S[i][j] == 2:
        cLCS(i-1,j,S,s1)
    else:
        cLCS(i,j-1,S,s1)
 
s1 = 'abcbdab'
s2 = 'bdcaba'
max,S = LCS(s1,s2)
print(S)
# print(len(S),len(S[0]))
cLCS(len(S)-1,len(S[0])-1,S,s1)
# print(max)

 

结果如下：

 

三、求字符串里的最长回文子串

题目：给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

举例：'cdca'的最长回文字符串为'cdc'

思路：遍历字符串的每个元素,然后以该元素为中心点进行左右扩展,取长度最大的

 

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution():
    def __init__(self):
        self.max_len = 0
        self.res = ''
 
    def getLongestPalindrome(self,s):
        if len(s) == 1:
            return
        start = 0
        for i in range(1,len(s)):
            tmp1 = self.max_side(s,i,i) #以这个数为中心点进行扩展
            if tmp1 > self.max_len:
                self.max_len = tmp1
                start = i - tmp1 // 2
 
            tmp2 = self.max_side(s,i-1,i)#从这个数和前面的数=以两个数为中心点进行扩展
            if tmp2 > self.max_len:
                self.max_len = tmp2
                start = i - tmp2 // 2
        self.res = s[start:start+self.max_len]
        return s[start:start+self.max_len]
 
    def max_side(self,s,i,j):
        maxs = 0
        if i == j: #单数是以一个数为中心
            maxs  = 1
            i -= 1
            j += 1
 
        while i >= 0 and j < len(s) and s[i] == s[j]: #双数以两个一样的字符为中心
            maxs += 2
            i -= 1
            j += 1
        return maxs
 
    #leetcode速度最快的代码
    def longestPalindrome_best(self, s):
        """
        :type s: str
        :rtype: str
        """
        length = len(s)
        if length < 2 or s == s[::-1]: return s
        max_len, begin = 1, 0
        for i in range(1, length):
            odd = s[i - max_len - 1:i + 1]
            even = s[i - max_len:i + 1]
            if i - max_len >= 1 and odd == odd[::-1]:
                begin = i - max_len - 1
                max_len += 2
                continue
            if i - max_len >= 0 and even == even[::-1]:
                begin = i - max_len
                max_len += 1
        return s[begin:begin + max_len]
 
S = Solution()
res = S.longestPalindrome_best(s='abaad')
print(res)

结果如下：aba

 

四、和为0的最长连续子串长度

题目：一个一维数组中只有1和-1，实现程序，求和为0的最长子串长度，并在注释中给出时间和空间复杂度

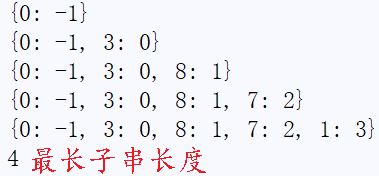
思路：在i从0到n，计算sum(i)，sum(i)表示从0到i的元素之和。并保存在字典dic中，value是索引i，在往后的遍历中每得到一个sum(i)就查看dic的keys是否已有此sum(i)值，如果有则用当前i位置减去保存的i，并与maxLen比较，取大的那个。遍历结束，给出结果。时间复杂度O(n)，空间复杂度O(1)

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def min_len(l):
    dic = {0: -1}
    sum = 0
    maxLen = 0
    for x in range(0, len (l)):
        sum += l[x]
        print(dic)
        if sum in dic:#如果有一样的数出现,说明两个数之间的数和第二个数之和等于0
            maxLen = max(maxLen, x - dic[sum])
        else:
            dic[sum] = x
    return maxLen
 
print(min_len([3,5,-1,-6,2]))

 

【扩展】和为给定值的最长连续子串

思路：遍历，找和为s的子串，留长度最大的

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def findarr(s,nums):
    if not nums:
        return 0
    res = -2 ** 31
    for i in range(4,len(nums)):
        pos = i + 1
        while pos < len(nums)-2 and sum(nums[i:pos+1]) < s:
            pos += 1
        if sum(nums[i:pos+2]) == s and pos - i + 1 > res:
            print(i,pos)
            res = pos - i + 1
    print(res)
 
s = 7
nums = [2,3,0,2,4,2,0,0,1,2,0,0,2,2]
findarr(s,nums)

 

　　

 

五、和大于等于给定值的最短连续子串

题目：给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组，返回 0。

举例：输入: s = 7, nums = [2,3,1,2,4,3]      输出: 2

解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。

思路1：遍历每位，找和大于等于给定值的长度，然后依次向后遍历，直到遍历完所有的位置。

思路2：滑动窗口，从左往右加到大于s的数，然后从左开始删,若删除之后还能得到大于s的数，则记录当前的长度,若不能，就继续右移,加数

 

思路1代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
def findarr(s,nums):
    # nums.sort() #[4,3,3,2,2,1]
    if not nums:
        return 0
    res = 2 ** 31
    for i in range(len(nums)):
        pos = i + 1
        while pos < len(nums)-2 and sum(nums[i:pos+1]) < s:
            pos += 1
        if pos - i + 1 < res:
            print(i,pos)
            res = pos - i + 1
    print(res)

　　

 思路2代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def minSubArrayLen2(s, nums):
    cur_sum = 0
    n = len (nums)
    res = float ("inf")
    l = 0
    for i in range (n):
        cur_sum += nums[i]
        while cur_sum >= s:
            res = min (res, i - l + 1)
            cur_sum -= nums[l]
            l += 1
    return res if res != float ("inf") else 0
 
s = 7
nums = [2,3,1,2,4,3]
res = minSubArrayLen2(s,nums)
print(res)

结果：res = 2　　

 

六、连续最大子序和

 题目：给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例: 输入: [-2,1,-3,4,-1,2,1,-5,4],  输出: 6

解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。

进阶: 如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。 O(n)

 

思路1：始终保留最大值，如果当前和比n还小，当前和就取n；否则，和加上这个数，然后用c_res记录最大子序列

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def maxSubArray1(nums):
    s, ts = - 2 ** 31, - 2 ** 31
    res_ = []
    c_res = []
    for n in nums:
        if n > ts + n:  #如果当前和比n还小，当前最大和就取n
            ts = n
            res_ = [n]
        else:   #否则，取n+ts
            ts = n + ts
            res_.append(n)
        if s < ts:
            s = ts
            c_res = list(tuple(res_))
            print("c_res=%s,res_=%s"%(c_res,res_))#c_res记录最大子序列
    return s
 
# res = maxSubArray1([1,-2])
# print(res)

　　

思路2：如果把数组分成左右两段，那么加和最大的连续子序列，要么出现在数组的左半部分，要么出现在数组的右半部分，要么出现在中间，即从左半部分和右半部分相邻的地方各区一段。所以可以用分治法来求解，具体实现时需要借助递归

代码如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import math
def CalMax(a, b, c):#三个数比较大小
    if a > b:
        if a > c:
            return a
        else:
            return c
    else:
        if b > c:
            return b
        else:
            return c
 
 
MaxLeftSum = 0
MaxRightSum = 0
number = [7, 0, 6, -1, 1, -6, 7, -5]
 
 
def MaxCalculator(left, right):
    middle = int(math.modf((left + right) / 2)[1])
    if left == right:
        if number[left] > 0:
            return number[left]
        else:
            return 0
 
    MaxLeftSum = MaxCalculator(left, middle)
    MaxRightSum = MaxCalculator(middle + 1, right)
    MLASum = 0
    MRASum = 0
    MSum = 0
 
    i = middle
    while i >= left:
        MSum += number[i]
        if MSum > MLASum:
            MLASum = MSum
        i = i - 1
    MSum = 0
 
    i = middle + 1
    while i <= right:
        MSum += number[i]
        if MSum > MRASum:
            MRASum = MSum
        i = i + 1
    return CalMax(MaxLeftSum, MaxRightSum, MLASum + MRASum)
 
n=6
result = MaxCalculator(0,n-1)
print(result)

结果：13

 

posted @   nxf_rabbit75  阅读(359)  评论(0)  编辑  收藏  举报
编辑推荐：
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语，封装的思维：从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热？
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 使用C#创建一个MCP客户端
· ollama系列1：轻松3步本地部署deepseek，普通电脑可用
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· 按钮权限的设计及实现
一、最长连续公共子串二、最长公共子序列(非必须连续)三、求字符串里的最长回文子串四、和为0的最长连续子串长度五、和大于等于给定值的最短连续子串六、连续最大子序和
点击右上角即可分享
微信分享提示
AI IDE Trae